可选交付方式及时间窗下城市配送服务选项多目标联合定价
邱晗光,高 敏,甄 杰,周继祥
(1.重庆工商大学 物流管理系,重庆 400067;2.重庆工商大学 市场营销系,重庆 400067;3.重庆工商大学 电子商务系,重庆 400067)
0 引言
随着线上超市、外卖、生活服务等新零售业态发展,顾客对城市配送末端交付方式与时间窗等服务选项存在差异化需求,例如餐食外卖更需要在偏好时段送货上门,而一般日用品包裹常常放在自提柜或自提点即可。顾客自选服务选项逐渐成为城市配送末端交付的发展趋势之一[1-2]。国内京东、菜鸟、顺丰,国外Tesco、ALDI、Sainsburys等企业已经开始为顾客提供不同的交付方式和精确到1小时的时间窗等服务选项,此类定制化配送订单的增长率在英国接近14%[3]。在普惠通用型配送服务的基础上,提供差异化服务选项,可以帮助供应商创新配送产品矩阵及盈利方式,同时也为服务供应商的运作管理带来了挑战。如何平衡配送成本与收益,成为服务供应商可持续性开展定制化配送的难题[4]。
在城市配送末端交付运作中,以更低的成本设计车辆调度及路径方案,是定制化配送可持续运营的前提之一[3]。以时间窗为例,鉴于顾客送达时间依赖于车辆访问顺序,基于地理位置主动引导顾客选择恰当的时间窗,对于获取具有成本优势的车辆路径方案有重要作用。相关研究也表明,顾客对于多个接近的时间窗没有明显偏好,时间窗差异化定价,直接影响顾客的选择行为[5]。在时间窗约束下,自提柜交付仅需在最晚配送时间之前送达,通常不存在最早配送时间约束,自提柜交付可以实现前置配送。使用价格手段,引导某些服务成本较高的送货上门交付转换为自提柜交付,对于提高顾客满意度、降低定制化配送运营成本具有重要作用。
目前,关于配送服务选项定价的研究主要关注送货上门交付(Attended Home Delivery, AHD)下的时间窗定价,该问题属于时间窗管理(Time Slot Management, TSM)领域的重要研究内容之一。时间窗管理研究将时间窗作为内生变量,主要关注时间窗宽度影响[6]、时间窗分配[7-10]、时间窗定价等问题,详细的研究总结可以参见文献[8,11-12]等。在此主要对时间窗定价的研究现状进行总结分析。
关于送货上门交付下,时间窗定价问题的研究大致可以分为静态定价和动态定价两类[13]。静态时间窗定价通常是离线基于预测数据进行的,首先建立顾客选择模型,然后构建收益模型进行定价,这类研究通常可以为时间窗长度、数量的设定及平峰时段的价格折扣等问题提供参考[4]。如朱恒恒等[14]基于不确定性期望效用理论和层次分析法(Analytic Hierarchy Process, AHP),提出关于时间窗价格和宽度的客户满意度模型,根据网络零售商收益偏好建立考虑客户满意度和期望收益的双目标时间窗定价模型;Klein等[3]使用基于秩次的方法描述了顾客对时间窗的选择行为,然后基于混合整数线性规划模型构建了时间窗定价模型。动态时间窗定价通常是在线基于实时订单进行的,需要根据到达订单的特点如地理位置、当前可用车辆、配送成本等,进行“一对一”的定价,当静态定价根据信息更新进行实时调整时也就演化为动态定价[4]。如Campbell等[5]考虑使用价格折扣,使消费者选择较宽的时间窗,进而降低配送路径的成本;徐朗等[15]考虑随时隙运力变化的需求特征以及客户与容量之间相互作用关系,建立了基于最大订单数量和最优时隙容量的动态定价模型;Yang等[4]使用离散多项选择模型描述顾客的选择行为,研究了时间窗价格折扣的动态优化设计及相应的配送成本预估算法,以引导顾客选择配送成本更低的时间窗。
本文的研究还涉及离散选择模型(discrete choice methods),该模型自提出以来逐渐成为定量化分析个体选择行为的重要工具,并根据应用需求从基本的多项Logit模型发展出了嵌套Logit模型、一般极值模型、混合Logit模型等[16-17]。在城市配送领域,早期主要使用多项Logit模型描述顾客对时间窗的选择行为,如Asdemir[18]。后来,鉴于多项Logit模型存在“与其他选择无关”的特性,研究开始使用嵌套Logit模型描述顾客选择配送服务的相关性,如陈淮莉等[19]考虑了顾客选择上午或下午时间窗的相关性;邱晗光等[20]考虑了顾客在选择末端交付方式和配送时间窗的相关性。
总体上看,时间窗定价的研究主要面向送货上门交付,这与国外以独立房屋居住为主的实际情况吻合。然而在中国城市化进程中,城市居民以高层建筑集中居住为主,考虑自提柜(Reception Boxes, RB)和送货上门组成的复合末端交付模式更符合国情。自提柜交付可以批量化操作,从操作耗时及配送距离来说,其运营成本通常低于送货上门交付,因此自提柜交付与送货上门交付的定价应该差异化。另外,在时间窗约束下,自提柜交付仅需在最晚服务时间之前送达,通常不存在最早服务时间约束,可以提前将包裹送往自提柜。因此,自提柜交付实行前置配送。运用价格手段引导某些服务成本较高的送货上门需求转换为自提柜交付,对于提高顾客满意度、降低定制化配送服务的运营成本具有重要作用。目前考虑末端交付方式及时间窗联合定价的研究还比较少。
本文首先构建了考虑配送服务选项联合定价的嵌套Logit模型,区分顾客选择交付方式和时间窗的相关性,量化考虑了服务定价的顾客选择行为;然后,考虑配送成本最小化和期望收益最大化,研究送货上门交付、自提柜交付及不同时间窗的多目标联合定价问题,以期为城市配送服务供应商开展定制化配送提供决策参考。
1 问题描述及参数定义
城市配送服务供应商在既定区域为顾客提供服务选项可定制的配送服务,包括送货上门(AHD交付)、自提柜(RB交付)两种末端交付方式(记为D={AHD,RB})和时间窗集合(记为SLOT),形成完整的服务选项集(记为D×SLOT)。其中,RB交付可以泛指无需顾客与配送人员面对面进行商品交接的交付方式,常见的小区门卫代收、公司代收、蚂蚁驿站等非接触交付方式均可归为此类。

根据问题描述,作如下假设:
假设1顾客i的位置为(xi,yj)、期望的时间窗为[earlyi,latei]、相互之间的路径距离dij是已知的(i,j∈Nc);
假设2不同末端交付方式与时间窗形成服务选项组合,包括顾客不指定时间窗的RB交付,记为(RB,Slot0);顾客指定时间窗s的RB交付,记为(RB,s);顾客指定时间窗s的AHD交付,记为(AHD,s);

假设4不同服务选项组合为顾客带来的基础效用存在差异,顾客不指定时间窗的RB交付基础效用为U1,顾客指定时间窗的RB交付基础效用为U2,顾客指定时间窗的AHD交付基础效用为U3。根据用户体验的差异,设定U1≤U2≤U3;
假设5根据自提柜距离、配送时间偏好及服务选项价格,顾客i选择不同服务选项组合的概率由嵌套Logit选择模型确定。
另外,使用完整有向图G=(N,AC)表示整个配送网络,模型使用的其他符号定义如下:
N表示点集;
N0表示配送中心,N0⊂N;
Nd表示自提柜集合,Nd⊂N;
Nc表示配送点或顾客集合,Nc⊂N,N0∪Nd∪Nc=N;
AC表示弧集,AC={(i,j):i,j∈N,i≠j};
dij表示配送点i和j之间的距离;
tij表示配送点i和j之间的行驶时间;
tsi表示配送点i的服务耗费时间,i∈Nc;
tai表示配送点i的到达时间,i∈Nc;
K={1,2,3,…,k},表示车辆集合;
C表示车辆载重能力。
2 模型建立
2.1 考虑配送服务选项联合定价的嵌套Logit模型
顾客对末端交付方式和时间窗的选择行为是相互影响的。若顾客对交付便捷性及配送时间精确性要求更高,通常选择AHD交付,如餐食外卖等;若顾客对交付便捷性和配送时间精确性要求不高,通常会选择RB交付,例如日用品包裹等。在考虑配送服务选项差异化定价的情形下,不同交付方式与时间窗组成的服务选项为顾客带来的效用不是独立的。使用两层嵌套Logit选择模型描述顾客选择行为,其中上层为不同的交付方式,下层为不同的时间窗,如图1所示。不失一般性,假设时间窗按时间从早到晚排序,即Slott-1早于Slott,其中在自提柜交付下,Slot0表示顾客不指定时间窗。



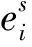
综上所述,顾客i分别选择不指定时间窗的RB交付、指定时间窗的RB交付和指定时间窗的AHD交付时,获得的总效用
(1)
根据效用最大化,顾客i选择不同交付方式的概率,如式(2)所示[21]:
(2)
顾客选择第d种交付方式下第s个时间窗的概率为
(3)
2.2 城市配送服务选项多目标联合定价模型
本文构建的多目标联合定价模型属于混合整数规划,以配送成本最小化和期望收益最大化为目标,优化不同顾客的交付方式和时间窗分配及相应的定价策略。
2.2.1 决策变量

(1)车辆路径变量
(4)
(2)交付方式变量
(5)
(6)
2.2.2 目标函数
构建的多目标联合定价模型目标函数分别如式(7)和式(8)所示:
(7)
(8)

2.2.3 约束条件
模型的约束条件可以分为服务需求类约束和车辆路径类约束。其中服务需求类约束如式(9)和式(10)所示:
(9)
(10)
约束(9)表示所有的配送点仅能选择送货上门或自提柜交付,不能重复选择。约束(10)表示所有选择送货上门的节点需要车辆直接服务,所有选择自提柜交付的节点无需车辆直接服务。
车辆路径类约束如式(11)~式(22)所示:
(11)
(12)
(13)
∀k∈K,t∈Nd;
(14)

(15)
(16)
∀s∈SLOT,∀(h,j)∈A;
(17)
earlyj≤taj≤lastj,∀j∈Nc;
(18)
lastm≤[lastizmi]-,∀m∈Nd,∀i∈Nc;
(19)
(20)
(21)
zmi∈{0,1},∀m∈Nd,i∈Nc,k∈K。
(22)
约束(11)表示网络节点流量平衡;约束(12)表示所有车辆必须从配送中心出发并回到配送中心;约束(13)表示送货上门交付的节点必须有车辆访问;约束(14)表示使用的自提柜必须有车辆访问,其中∪表示逻辑并运算;约束(15)表示车辆载重约束;约束(16)避免车辆出现子回路,Vk表示车辆k访问的任一节点集合;约束(17)表示车辆到达时间约束(仅约束送货上门交付节点),其中tah、taj分别代表到达配送点h和j的时刻,tsh表示配送点h的服务时间,thj表示从配送点h到配送点j的时间;约束(18)表示送货上门交付节点的时间窗约束;约束(19)表示自提柜的最晚服务时间必须早于所有其服务顾客的最晚服务时间(仅约束自提柜交付节点);约束(20)~约束(22)表示决策变量的取值范围。
3 仿真分析
本文构建的城市配送服务选项多目标联合定价模型主要运用多目标遗传算法和粒子群算法进行求解。仿真分析采用MATLAB R2019a版本,使用MATLAB脚本语言进行仿真实现;仿真环境为IntelCore i7-6700k CPU、16 G内存和Window10专业版。结合文献[19]研究成果、嵌套Logit模型中尺度参数的取值范围[17]及车辆实际情况,仿真过程中涉及的参数如表1所示。

表1 仿真分析相关参数
3.1 仿真算例设计
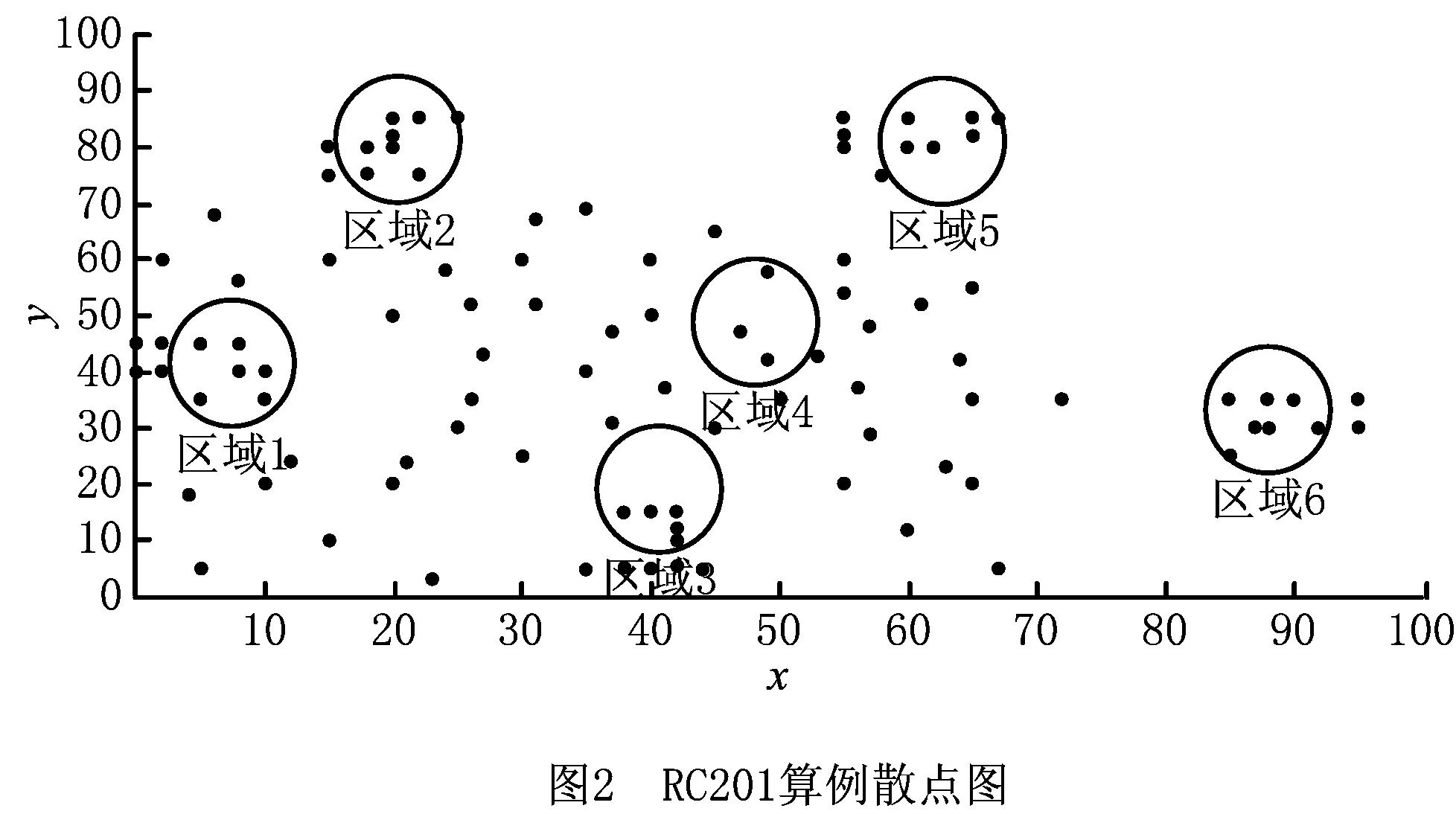
仿真算例基于Solomon标准库RC201和RC206算例设计。RC201和RC206算例分别有100个配送点和50个配送点,其分布位置如图2和图3所示。图2中,RC201算例从6个配送点较密集的区域分别选择1个配送点设立自提柜(共计6个自提柜);图3中,RC206算例从5个配送点较密集的区域分别选择1个配送点设立自提柜(共计5个自提柜)。

3.2 仿真算法设计
在仿真分析中,分别使用多目标粒子群优化算法(Multiple Objective Particle Swarm Optimization, MOPSO)和MATLAB自带的遗传算法工具箱求解构建的配送服务选项多目标联合定价模型。MATLAB遗传算法工具箱中,多目标问题求解可以使用gamultiobj函数[22],该函数能够便捷地获取帕累托前沿,并进行可视化。
MOPSO算法是Sierra和Colle等在求解单目标优化的基本粒子群算法基础上,通过设计合理的Pareto集多样性维持策略和粒子群全局最优值更新操作而提出的[23-24]。MOPSO算法基于动态网格技术在粒子数最少的网格内随机选择全局极值,在进化过程中自适应调整网格进行粒子的动态划分[23]。MOPSO算法采用的编码方法可以参见文献[25],算法流程如图4所示。

3.3 计算结果
采用MOPSO算法和MATLAB自带的gamultiobj遗传算法在RC201和RC206算例中获取的帕累托前沿分别如图5和图6所示。

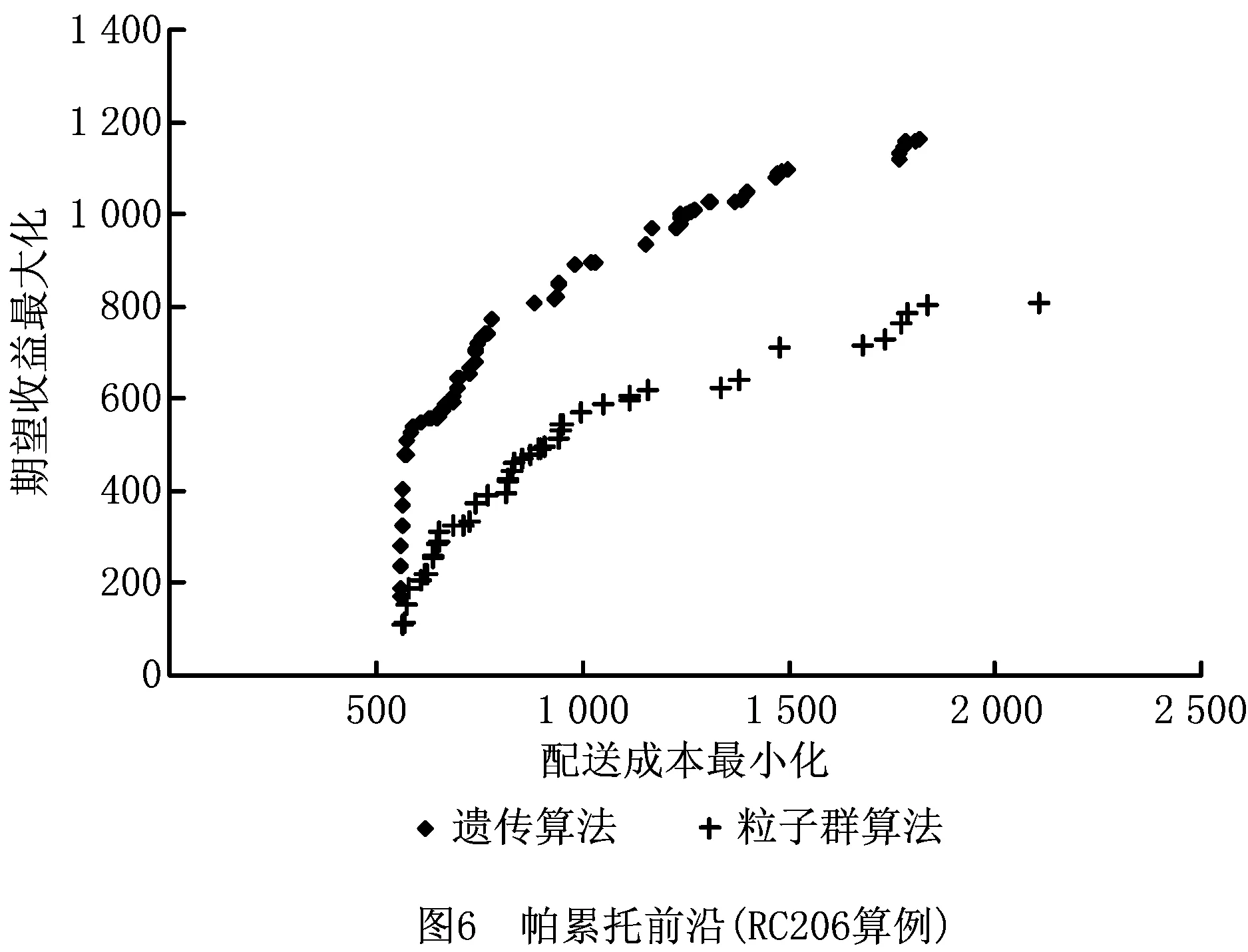
从图5和图6可知,无论RC201算例还是RC206算例,没有找到在配送成本最小化和期望收益最大化两个目标上均占优的帕累托解;从算法性能来看,遗传算法获取的帕累托前沿均在粒子群算法上方,在两个算例中,遗传算法获取的帕累托解集合均优于粒子群算法。后续尺度因子的敏感性分析采用MATLAB提供的遗传算法完成。
3.4 送货上门尺度因子对服务选项联合定价的影响
在考虑配送服务选项联合定价的嵌套Logit模型中,送货上门尺度因子θAHD表示顾客选择送货上门交付时不同时间窗的替代性。
(1)送货上门尺度因子对AHD交付定价的影响
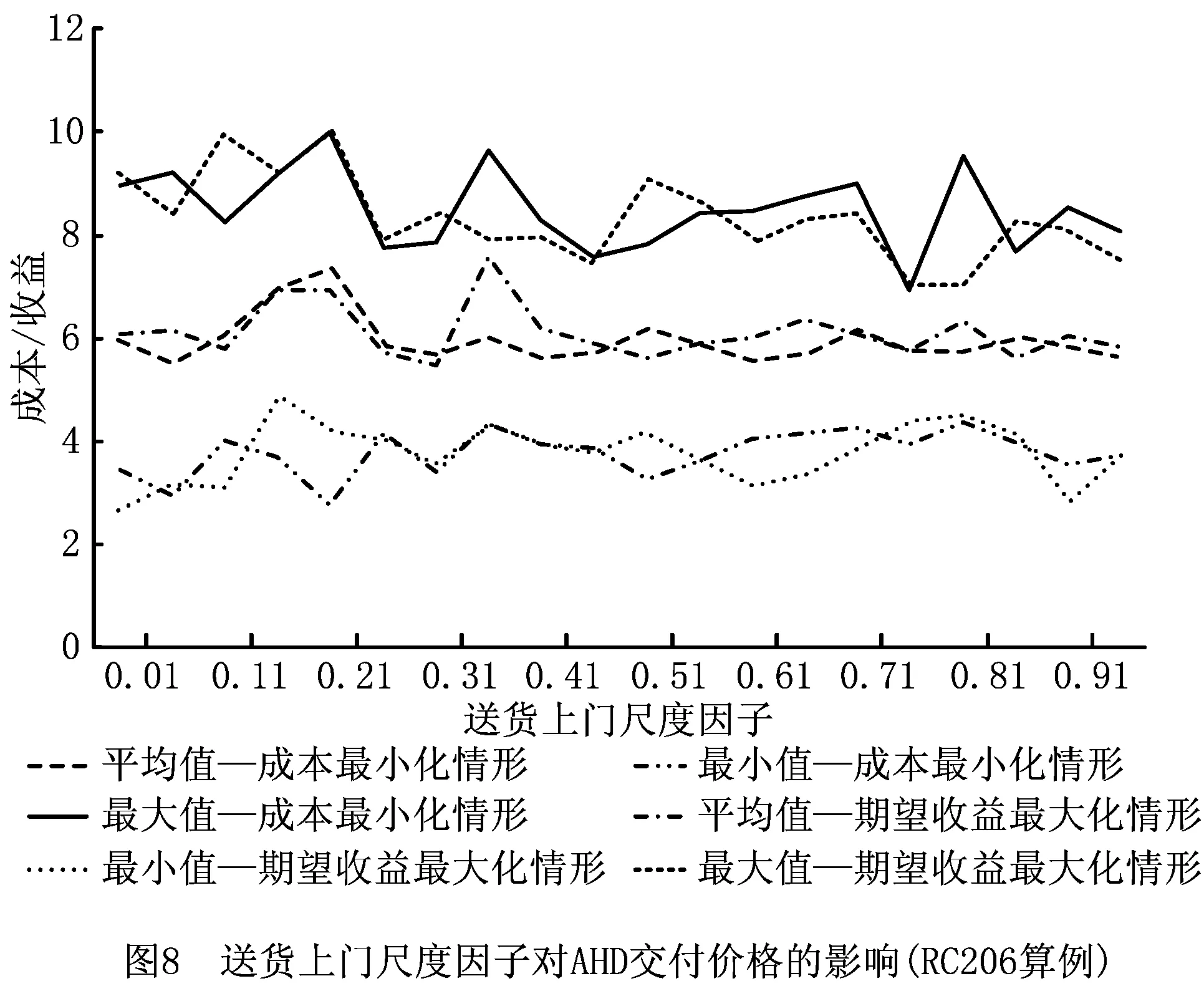
图7和图8所示为配送成本最小化和期望收益最大化情形下,RC201和RC206算例中AHD交付定价的最大值、最小值和平均值随送货上门尺度因子的变化情况。随着送货上门尺度因子逐渐增大,AHD交付最优定价的最大值呈现震荡下降的趋势,而平均值和最小值的变化趋势不太明显。
随着送货上门尺度因子逐渐增大,顾客对于不同时间窗的选择替代性越来越小,顾客更加看重配送是否在偏好的时间窗内送达,定价因素对顾客选择行为的影响越来越小。调整AHD交付定价不能明显改变顾客的选择行为,难以实现成本最小化和期望收益最大化的帕累托改进。因此,送货上门尺度因子对AHD交付定价的影响不太明显。

(2)送货上门尺度因子对时间窗定价的影响
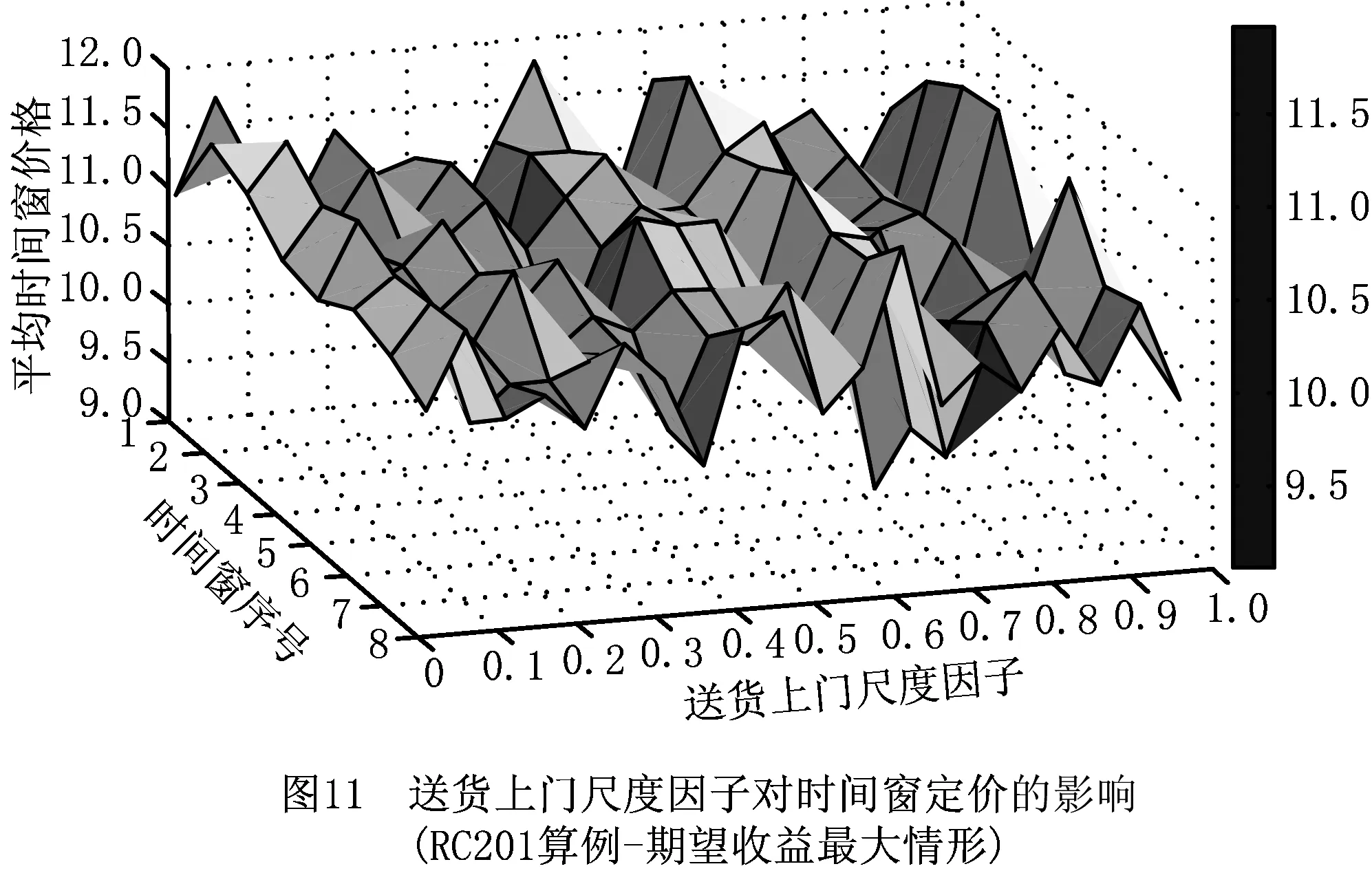
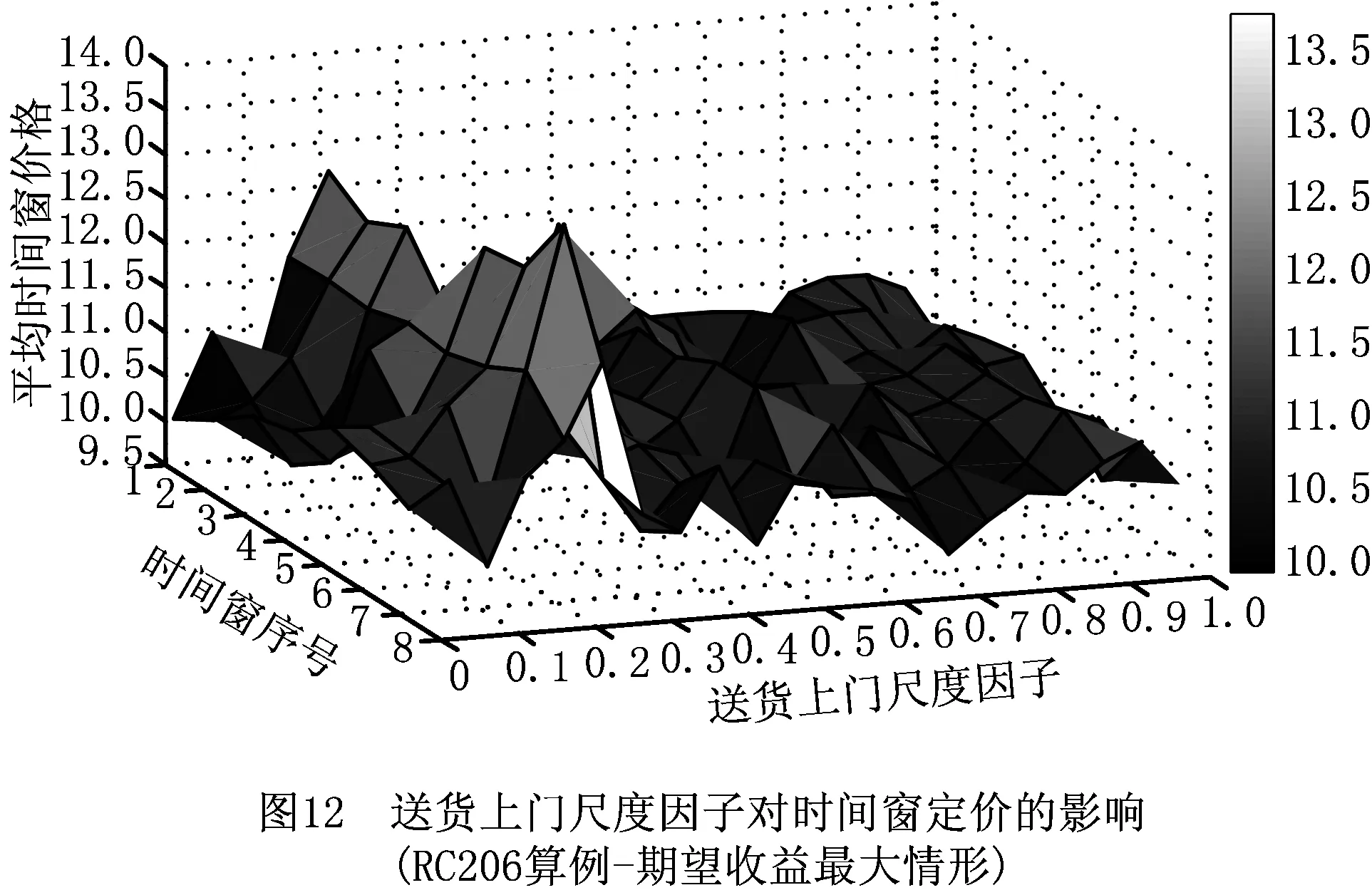
图9~图12所示为配送成本最小化和期望收益最大化情形下,RC201和RC206算例中不同时间窗定价平均值随送货上门尺度因子的变化情况。仿真分析中,配送中心在单个配送周期内运作时间共计960 min;按照时间窗长度120 min计算,时间窗数量为8个。
从图9和图11可以看出,RC201算例中,随着送货上门尺度因子逐渐增大,时间窗定价在偏好配送成本最小化时呈现震荡降低的趋势,在偏好期望收益最大化时变化趋势并不明显;从图10和图12可以看出,RC206算例中,时间窗定价随着送货上门尺度因子的变化趋势不如RC01算例明确,但是总体而言,在区间θAHD∈[0.1.0.4]内时间窗定价的平均值还是高于区间θAHD∈[0.5.1]。因此,送货上门尺度因子对时间窗定价的影响不存在明显趋势。
随着送货上门尺度因子逐渐增大,顾客选择替代性越来越小,顾客在AHD交付下选择非偏好时间窗的概率越来越小,定价因素对顾客选择行为的影响也越来越小。因此,时间窗定价随着送货上门尺度因子增大的变化趋势不明确。


3.5 自提柜交付尺度因子对服务选项联合定价的影响
在考虑配送服务选项联合定价的嵌套Logit模型中,自提柜交付尺度因子θrd表示顾客在选择自提柜交付时不同时间窗的替代性。
(1)自提柜交付尺度因子对AHD交付定价的影响
图13和图14所示为配送成本最小化和期望收益最大化情形下,RC201和RC206算例中自提柜交付价格的最大值、最小值和平均值随尺度因子的变化情况。无论是最大值、最小值还是平均值,随着自提柜交付尺度因子的变化,RC201和RC206算例中AHD交付定价的变化趋势均不太明显。
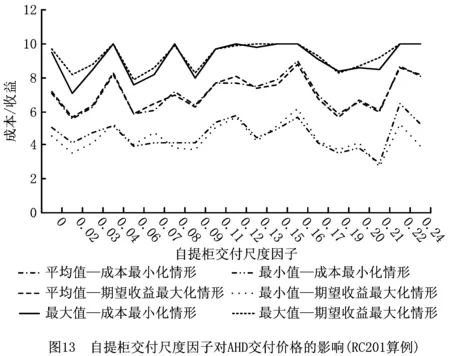

不同于送货上门尺度因子,自提柜交付尺度因子对AHD交付定价的影响较小。随着自提柜交付尺度因子逐渐增大,顾客选择替代性越来越小。由于自提柜交付下送达时间仅需在顾客偏好的最晚服务时间之前送达,在实际运作中自提柜交付下时间窗的约束是半开放式的,需要满足的时间窗约束弱于AHD交付,自提柜交付尺度因子增大的影响也随之被弱化了。因此,AHD交付定价的变化趋势并不明显。
(2)自提柜交付尺度因子对时间窗定价的影响
图15~图18所示为配送成本最小化和期望收益最大化情形下,RC201和RC206算例中不同时间窗定价平均值随自提柜交付尺度因子的变化情况。在RC201和RC206算例中,随着自提柜交付尺度因子逐渐增大,无论是配送成本最小化情形,还是期望收益最大化情形,时间窗定价均呈现震荡上升趋势。




由于自提柜交付下送达时间仅需在顾客偏好的最晚服务时间之前送达,实际运作中满足顾客自提柜交付下时间窗需求的时间窗有多个,例如顾客偏好的时间窗为[12:00,14:00],但是配送在早于14:00之前的时间窗到达均符合约束,包括[10:00,12:00]、[12:00,14:00]等。因此,随着自提柜交付尺度因子增大,虽然顾客在不同时间窗之间的替代性减少,但是顾客在偏好时间窗进行配送的概率变化并不大。此时,适当提高时间窗定价,不但不会明显降低顾客的期望配送数量,还会提高帕累托解集的期望收益。
4 结束语
顾客自选末端交付方式和时间窗,是城市配送服务供应商从通用型配送服务向定制化差异服务转型的重要措施,符合当前“线下+线上”新零售融合发展的趋势。考虑送货上门和自提柜两种交付方式及时间窗等服务选项,本文将定制化配送细分为不指定时间窗的自提柜交付、指定时间窗的自提柜交付和指定时间窗的送货上门交付。构建了考虑服务选项联合定价的嵌套Logit选择模型,描述了服务选项定价对顾客选择行为的影响。考虑配送成本最小化和期望收益最大化,建立了基于混合整数规划的城市配送服务选项多目标联合定价模型,在优化车辆配送路径的同时,讨论了顾客末端交付方式和时间窗分配策略及对应的联合定价决策。使用遗传算法和粒子群算法对Solomon标准库中RC201和RC206算例进行数值求解。仿真数据表明:RC201和RC206算例均能获取帕累托前沿,在求解性能上遗传算法优于粒子群算法;随着送货上门尺度因子增加,不同时间窗的选择替代性越来越小,定价因素对顾客选择行为的影响越来越小,送货上门交付定价与时间窗定价的变化趋势不明显;由于自提柜交付下送达时间仅需在顾客偏好的最晚服务时间之前送达,需要满足的时间窗约束弱于AHD交付,自提柜交付尺度因子的变化影响也就随之被弱化了,对送货上门交付定价的影响也不明显;随着自提柜交付尺度因子增大,虽然顾客在不同时间窗之间的替代性减少,但是顾客在偏好时间窗进行配送的概率变化并不大,适当提高时间窗定价,并不会明显降低顾客的期望配送数量,故时间窗定价随着该因子的增长呈现震荡上升趋势。未来,关于定制化城市配送服务选项定价的研究还可以关注不同交付方式、不同时间窗定价的交叉影响关系,以及在顾客配送需求时变情形下如何进行差异化定价以平衡服务能力与配送需求。

