基于时间向量的多工序加工系统工艺路线重组建模与优化

段建国，王彦森，谢 楠

(1.上海海事大学 中国(上海)自贸区供应链研究院，上海 201306；2.上海海事大学 物流工程学院，上海 201306；3.同济大学 中德工程学院，上海 201804)

0 引言

工艺是设计和制造的桥梁，也是一切生产活动的基础。创新工艺技术不仅能够使企业大幅降低制造成本、提升制造效率、减少能源消耗与环境污染，还是实现制造业可持续发展，提升绿色制造水平的基本方式[1]。目前，大多数工艺制定过程均在假定企业生产车间具有足够资源的状态下进行，是一种静态的工艺规划，并没有考虑企业制造资源的实时状态。另外，指定工艺路线一般是在车间生产之前完成的，即使在指定工艺路线时考虑到车间的实际情况，也无法避免车间在工艺路线规划与工艺路线实施两过程之间企业资源状态发生改变，这种动态的变化可能使原先的工艺路线失去意义，甚至无效[2-4]。

不断变化的动态市场需求以及车间加工环境中的加工系统需要不断地从一种状态转变为另一种状态，以适应动态的生产需求，这就要求在尽量重用现有工艺的基础上，提高工艺设计的效率，降低工艺规划过程的复杂性。因此，如何快速重组工艺路线，实现加工过程动态实时响应具有十分重要的理论和现实意义。Eimaraghy[5]根据传统静态的零件族、组合零件以及标准工艺规程文件等定义，提出了“进化零件/零件族”和“可重组工艺规划”的概念，并指出可重组工艺规划是连接零件和制造系统的进化性、可重组性的桥梁。在现有工艺的基础上，经过加工特征的添加、移除，并利用加工特征优先图能否实现工艺路线的重排取决于产品变化范围和程度，以及需求生产批量大小。这两个因素决定了需求工艺、安装、夹具的变化程度和成本，也决定了满足产品变化所要经历的工艺变化过程[6]。Azab等[7-9]在给定工艺规划可重组性指数的基础上，利用原零件族的标准工艺规程建立了面向进化零件族的单工序加工系统的可重组工艺规划(Reconfigurable Process Planning, RPP)模型;Musharavati等[10-11]结合启发式知识和元知识等辅助知识，利用模拟退火技术中的基因组合设计了3种改进的模拟退火算法，来解决工艺优化问题;Shabaka等[12-13]提出了工艺规划和模块化机床集成设计的方法，通过加工特征与机床模块的映射实现加工操作的组合;徐立云等[14-15]在现有制造资源(加工设备、刀具、夹具等)基础上，根据各工位装夹方式，通过加工操作聚类和分类，增加并行工位，以各工位间加工操作的转移实现工艺重构;刘金峰等[16]以工序加工知识单元为对象，提出了基于加工特征的工艺信息重用方法。

以上研究主要是针对单工序加工系统进行。与单工序加工系统不同，在多工序加工系统中，毛坯顺序通过预先制定的各道工序后得到最终产品，其产量、功能以及质量受系统中所有工序的共同作用，如零件材料特性、工装设备、夹具元素特征、刀具类型、零件位置姿态等，不同工序间存在着复杂的耦合关系。本文以多工序加工模式为背景，针对加工工序和影响因素繁多等特点，为提高工艺规划的柔性、可重用性及动态适应性，在文献[17]的基础上对多工序加工系统工艺路线重组建模方法进行了进一步的研究，设计了工艺路线整数线性优化重组算法，并结合汽车发动机缸盖加工工艺优化重组验证了所建重组模型和优化算法的有效性。

1 模型建立

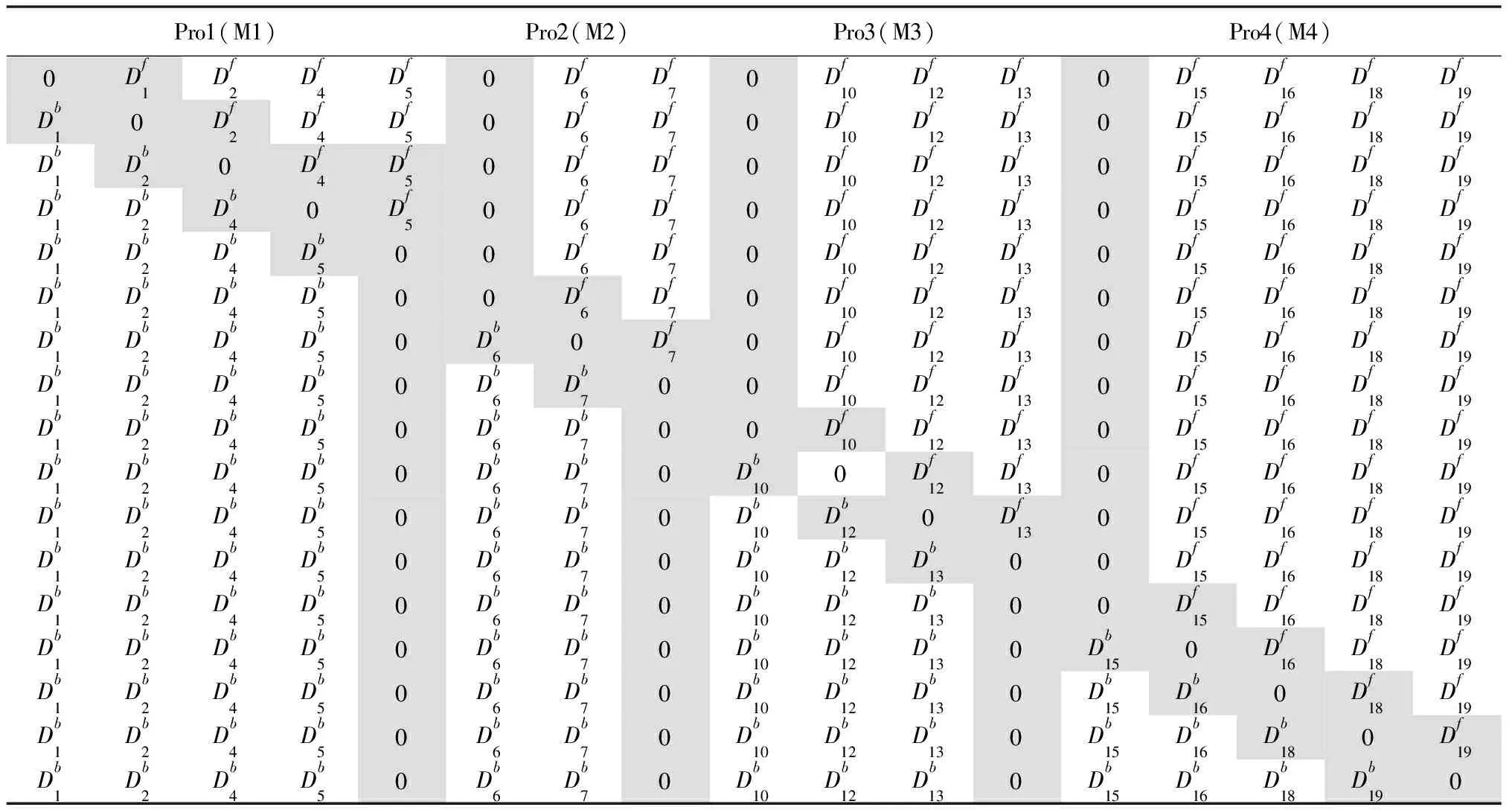
假设某零件工艺路线中包括4道工序：立式加工中心(M1)、立式加工中心(M2)、立式加工中心(M3)、卧式加工中心(M4)各一台，每道工序执行若干加工操作任务(s1～s19)。现要加工一新型相似零件，要求该类型零件与原零件族实现共线生产。假设已知原零件族的工艺路线，且该工艺路线经过简化后如表1所示，表中阴影部分为新零件没有的加工操作任务，剩余的加工操作任务与新零件的相似或相同。

表1 简化后的工艺路线

从生产效率上讲，非加工时间完全多余，应当尽力缩短。如果一条生产线存在大量的非加工时间，将大幅降低企业的生产效率。只有尽量消除瓶颈，缩短非加工时间造成的浪费，才能提高效率，获取最大的利润。因此，在零件族更新后，为了实时地响应生产要求，在充分利用原零件族工艺知识的基础上，应尽量缩短非切削时间和空闲时间等闲置时间。

为了便于对多工序加工系统的工艺路线重组过程进行讨论和建模，下面对相关变量、目标函数与约束条件进行阐述。

1.1 变量

q为工序数;

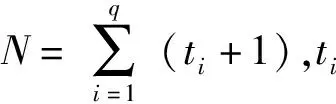
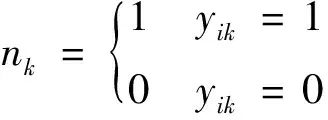
Dij为新加工操作任务插入第i个位置时，与第j个任务之间约束关系被破坏而引入的惩罚时间；

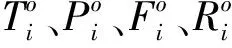
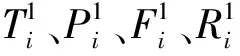
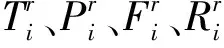
Cij为新加工操作任务插入第i个位置时第j个任务的实际加工时间；

Ck为新加工操作任务插入位置i时第k道工序的加工时间；

Ak为第k道工序中变量j的取值集合。

1.2 非切削时间目标函数

对第1个待加工操作任务可能的插入位置进行标注(如表2阴影部分)。

表2 可能的位置

新加工操作任务插入后会对加工操作任务的优先关系、换刀、定位、装夹、工作台旋转等操作时间产生一系列的影响，具体分析如下：

(1)优先关系惩罚项 在插入位置插入加工操作任务不仅可能破坏该位置前后任务的优先关系，还可能破坏该加工操作任务与其他任务的优先关系。为了保证形式的稳定性，构造N×N维惩罚时间矩阵如下：

Pro1(M1)Pro2(M2)Pro3(M3)Pro4(M4)0Df1Df2Df4Df50Df6Df70Df10Df12Df130Df15Df16Df18Df19Db10Df2Df4Df50Df6Df70Df10Df12Df130Df15Df16Df18Df19Db1Db20Df4Df50Df6Df70Df10Df12Df130Df15Df16Df18Df19Db1Db2Db40Df50Df6Df70Df10Df12Df130Df15Df16Df18Df19Db1Db2Db4Db500Df6Df70Df10Df12Df130Df15Df16Df18Df19Db1Db2Db4Db500Df6Df70Df10Df12Df130Df15Df16Df18Df19Db1Db2Db4Db50Db60Df70Df10Df12Df130Df15Df16Df18Df19Db1Db2Db4Db50Db6Db700Df10Df12Df130Df15Df16Df18Df19Db1Db2Db4Db50Db6Db700Df10Df12Df130Df15Df16Df18Df19Db1Db2Db4Db50Db6Db70Db100Df12Df130Df15Df16Df18Df19Db1Db2Db4Db50Db6Db70Db10Db120Df130Df15Df16Df18Df19Db1Db2Db4Db50Db6Db70Db10Db12Db1300Df15Df16Df18Df19Db1Db2Db4Db50Db6Db70Db10Db12Db1300Df15Df16Df18Df19Db1Db2Db4Db50Db6Db70Db10Db12Db130Db150Df16Df18Df19Db1Db2Db4Db50Db6Db70Db10Db12Db130Db15Db160Df18Df19Db1Db2Db4Db50Db6Db70Db10Db12Db130Db15Db16Db180Df19Db1Db2Db4Db50Db6Db70Db10Db12Db130Db15Db16Db18Db190

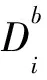
如果新加工操作任务插入后会破坏该任务与其他任务的优先关系，则为Dij赋一个比较大的数值，如1 000 s；否则，Dij=0 s。惩罚时间为

(1)

(2)换刀项 为了建模方便，使向量元素个数与待插入位置数相等，将换刀时间向量分为左、右两部分，分别指新加工操作任务与左右相邻任务之间由于换刀而产生的换刀时间向量。当不需要换刀时，Ti=0。

1)原换刀时间向量如下：

Pro1(M1)Pro2(M2)Pro3(M3)Pro4(M4)To1To2To3To40To6To70To9To10To110To13To14To15To160

2)左换刀时间向量如下：

Pro1(M1)Pro2(M2)Pro3(M3)Pro4(M4)Tl1Tl2Tl3Tl4Tl5Tl6Tl7Tl8Tl9Tl10Tl11Tl12Tl13Tl14Tl15Tl16Tl17

3)右换刀时间向量如下：

Pro1(M1)Pro2(M2)Pro3(M3)Pro4(M4)Tr1Tr2Tr3Tr40Tr6Tr70Tr9Tr10Tr110Tr13Tr14Tr15Tr160

换刀时间增量为

(2)

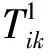
(3)

后续将通过建立类似形式的时间向量计算定位时间增量、装夹时间增量和工作台旋转时间增量。

(3)定位项 定位时间增量为

(4)

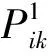
(5)

(4)装夹项 装夹时间增量为

(4)

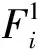
(5)工作台旋转项 当新加工操作任务插入到含有回转工作台的机床进行加工时，如果插入位置前后加工操作任务的进刀方向(Tool Approach Direction, TAD)与新插入加工操作任务的TAD不同，就会产生工作台旋转时间。如果待插入位置所对应的机床回转工作台可实现该旋转操作时，可根据实际情况确定该时间；否则，赋一较大值。

工作台旋转时间增量为

(5)

综合优先关系惩罚项、换刀项、定位项、装夹项以及工作台旋转项，可以得到新生成的工艺路线的非切削加工时间目标函数

(6)

1.3 生产线空闲时间目标函数

新加工操作任务不但对插入位置两侧任务的加工时间有影响，对其自身和其他任务的加工时间亦可能产生影响。因此，构造加工时间矩阵如下：

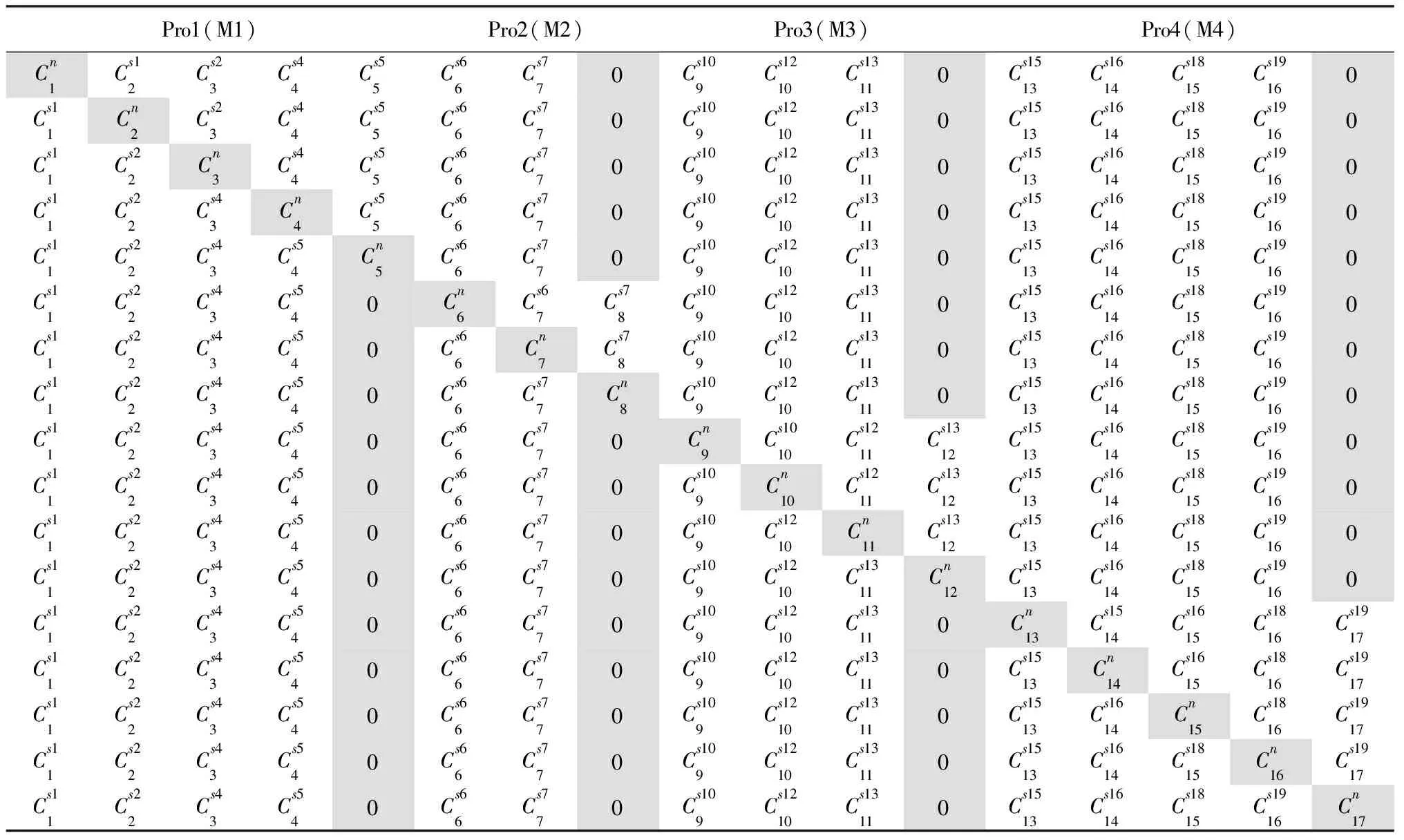
Pro1(M1)Pro2(M2)Pro3(M3)Pro4(M4)Cn1Cs12Cs23Cs44Cs55Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cn2Cs23Cs44Cs55Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cn3Cs44Cs55Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cn4Cs55Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs54Cn5Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cn6Cs67Cs78Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cs66Cn7Cs78Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cs66Cs77Cn8Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cs66Cs770Cn9Cs1010Cs1211Cs1312Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cn10Cs1211Cs1312Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cs1210Cn11Cs1312Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cs1210Cs1311Cn12Cs1513Cs1614Cs1815Cs19160Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cs1210Cs13110Cn13Cs1514Cs1615Cs1816Cs1917Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cs1210Cs13110Cs1513Cn14Cs1615Cs1816Cs1917Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cn15Cs1816Cs1917Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cn16Cs1917Cs11Cs22Cs43Cs540Cs66Cs770Cs109Cs1210Cs13110Cs1513Cs1614Cs1815Cs1916Cn17

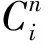
通过分析加工时间矩阵可以得到新加工路线中每道工序的加工时间为

(7)

以上述给定的加工时间矩阵为例，C1、C2、C3、C4分别为：

新加工操作任务的引入有可能会对其他任务的加工时间产生影响，比如加工过程具有逻辑关系的加工操作任务。新任务的加工时间取决于插入位置所处工序机床的加工能力，需要通过依据一定的工艺参数计算后确定。如果不考虑新加工操作任务对其他任务加工时间的影响，加工时间矩阵可简化为原加工操作任务时间向量和新加工操作任务插入所有待插入位置后生成的待加工操作任务时间向量，此时每道工序的加工时间可简化为

(8)

式中Cj为第j个加工任务的加工时间。

当一条生产线中每道工序所对应的机床加工能力不一致时，就会产生空闲时间。瓶颈工序决定了整条生产线的加工能力，为了衡量生产线平衡状况，建立总空闲时间目标函数

(9)

式中：CT为生产节拍；Tk为第k道工序的总加工时间；mk为第k道工序中并联机床的数目；每道工序的加工时间为

(10)

设I(·)为示性函数。当j∈Ak时，I(j:j∈Ak)=1；当j∉Ak，I(j:j∈Ak)=0。在所建立的数学模型中，待插入位置所处工序k的决策变量yik和变量j的取值范围Ak是相关的，即当j∈Ak时，yik=I(j:j∈Ak)=1；当j∉Ak，yik=I(j:j∈Ak)=0。

1.4 约束条件

每一个待加工操作任务只能插入一次，即

(11)

每一道工序总加工时间不能超过生产线的节拍时间，即

Tk≤mk·CT。

(12)

传统工艺路线重新排序或者一次插入全部待加工操作任务的工艺路线重组为NP难问题，但可重组工艺规划数学模型是P问题，求解难度明显降低。目标函数为

minF=αG+βIT。

(13)

式中：α为非切削时间目标函数系数(0<α<1);β为生产线平滑指数系数(0<β<1)，α+β=1。

2 算法设计

根据第1章给出的数学模型式(13)可以看出，该模型为0-1整数线性规划问题，既可以用智能算法求解，如遗传算法、模拟退火算法等，也可以通过整数线性规划算法进行求解，如分支定界算法、割平面方法等。智能算法只能求得全局近似最优解，而整数线性规划算法可求得全局最优解。另外，考虑到待解模型的规模及约束的特殊性，采用改进的分支定界算法进行求解，算法的具体步骤如下：

步骤1初始化待插入加工任务数目OP=M、惩罚时间矩阵和加工时间矩阵D=C=0、换刀时间向量Tl=Tr=To=0、定位时间向量Pl=Pr=Po=0、装夹时间向量Fl=Fr=Fo=0、工作台旋转时间向量Rl=Rr=Ro=0、m=n=1。

步骤2判断待插入加工任务的数量OP是否为空，是则停止程序，输出所有待加工任务插入完全后所有的最优工艺路线xm(m=1～M)及其最优函数值vm；否则，转步骤3。

步骤3根据加工任务的自由度及优先关系约束，确定所有待加工任务插入的先后顺序，并选择待加工任务OPm进行插入操作。

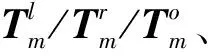
步骤5原模型的线性规划松弛可记作：

mineTx;

s.t.

aTx=1,

cTx≤d,

x∈[0,1]N。

其中：ci>0，ai>0，i=1,…,N。由于该模型约束的特殊性，在此利用贪婪法求解，不必利用单纯形算法。设{ei/ci}按降序排列，利用贪婪算法求解此线性规划松弛模型，得到最优解x*及其对应的下界v*。

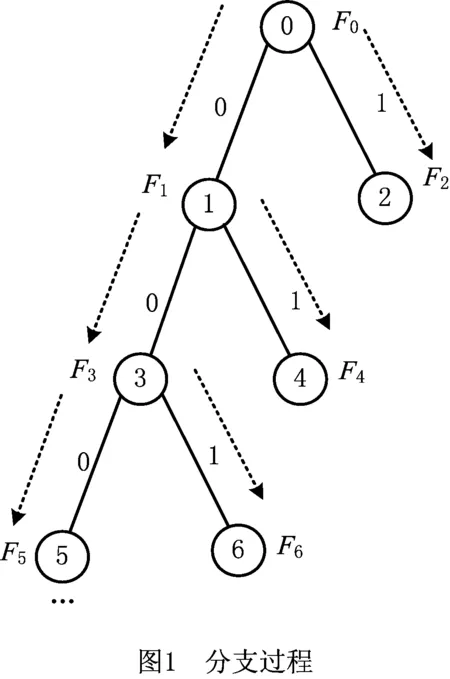
步骤6判断最优解x*中各元素是否为整数，如果是，该最优解即为原0-1整数规划模型最优解，记vm=v*，xm=x*，令m=m+1，转步骤2；否则，在x*中选择变量分数xi进行分支，分别固定xi=0和xi=1得到两个子问题P1和P2，如图1所示。

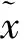
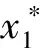
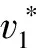
4 案例分析

现有一待加工4缸柴油发动机缸盖，包含上下平面、左右侧面、前后端面、挺杆孔、电热塞孔、进/排气座圈孔等大量的形状和精度特征信息，毛坯类型为铸件，材料类型为HT250，基体尺寸分别为：长544 mm、宽214 mm、高95 mm。原有一款相似缸盖产品，其材料类型、毛坯类型、生产类型以及选用的加工资源(不包括刀具)与待加工零件一致，选用的刀具资源略有不同，基体尺寸分别为：长481 mm、宽184 mm、高85 mm，其机械加工工艺如表3所示。

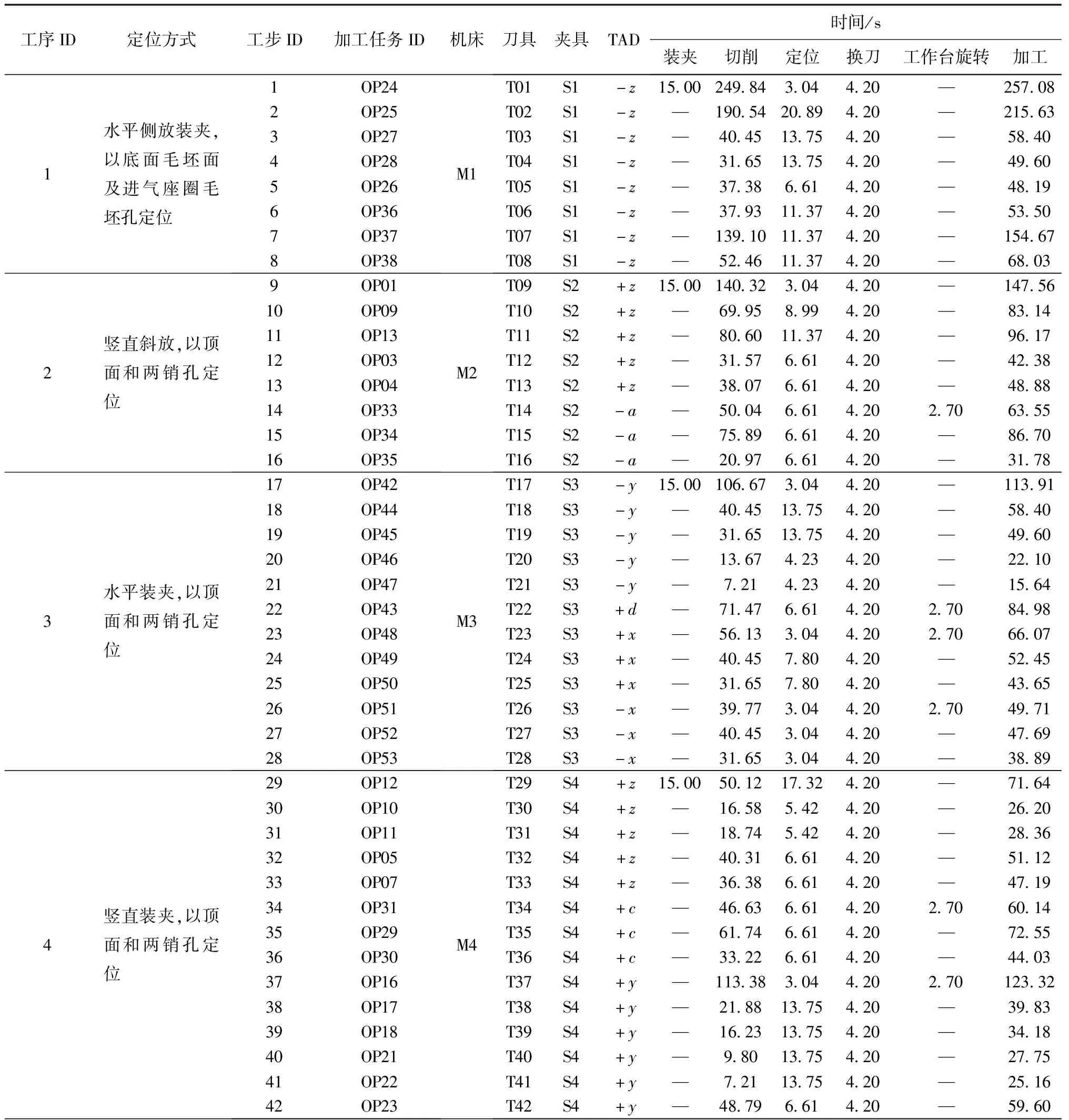
表3 相似缸盖产品的机械加工工艺

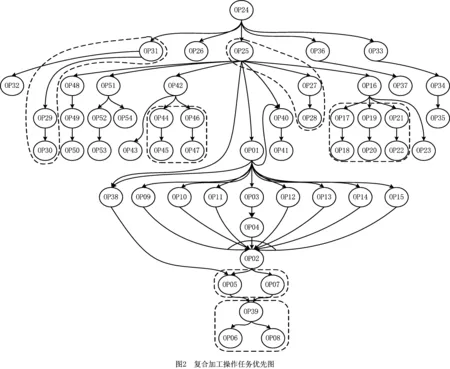
依据待加工缸盖产品材料类型、尺寸、行为公差、硬度等要求以及工艺文件中规定的工序要求、刀具材料、刚性、直径、齿数、有无冷却液和加工设备，通过查阅切削手册，利用相关公式计算出切削速度、主轴转速和切削时间。比如4-进气座圈孔的加工包括镗和铰两步，时间分别为41.13 s、151.81 s；4-喷油器孔的钻孔时间为44.14 s，铰孔时间为98.78 s。新加工操作任务相关可选加工信息如表4所示，两零件的加工操作任务信息及其复合加工操作任务优先关系如图2所示。

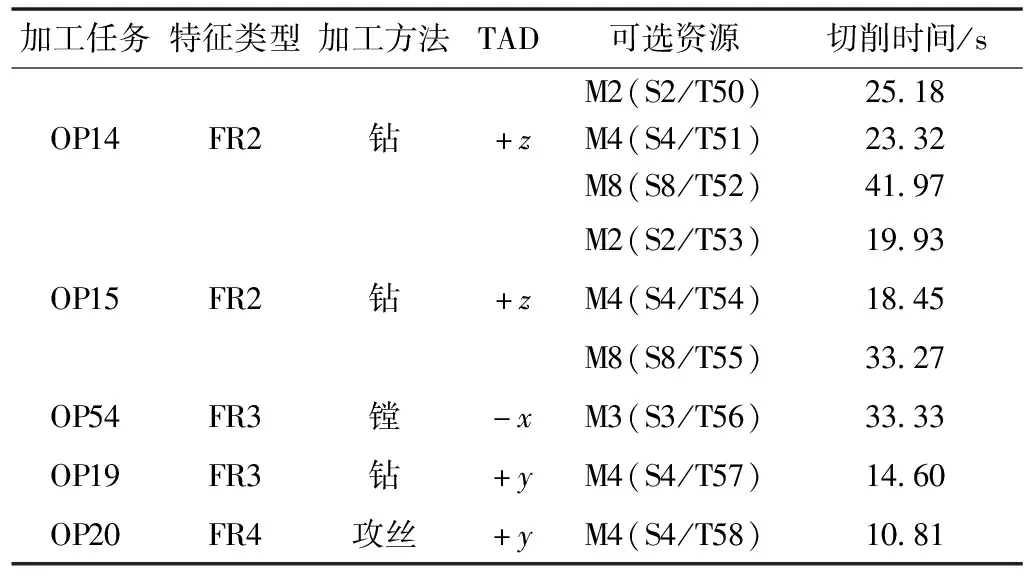
表4 新加工任务及其可选资源

记本文所提工艺路线重组模型为模型1，生成结果记为工艺路线1。利用本文所提方法对相似工艺实例进行重组，根据复合加工任务优先图，将重组过程设定为OP14→OP15→OP19→OP20。重组后的加工工序时间与相似缸盖零件加工工序时间如图3所示。从图3可以看出，待加工缸盖的所有加工特征均可在原设备及生产线上实现，且在所有工序中两者的加工时间基本一致。

此外，分别采用基于遗传算法[18]和模拟退火算法[8]对全部待插入操作一次性插入工艺路线的重组模型(记为模型2)以及传统的工艺路线重新排序模型(记为模型3)进行优化，优化结果分别记为工艺路线2和工艺路线3，则三者的最终工艺路线及其工序时间信息分别如表5和图4所示。

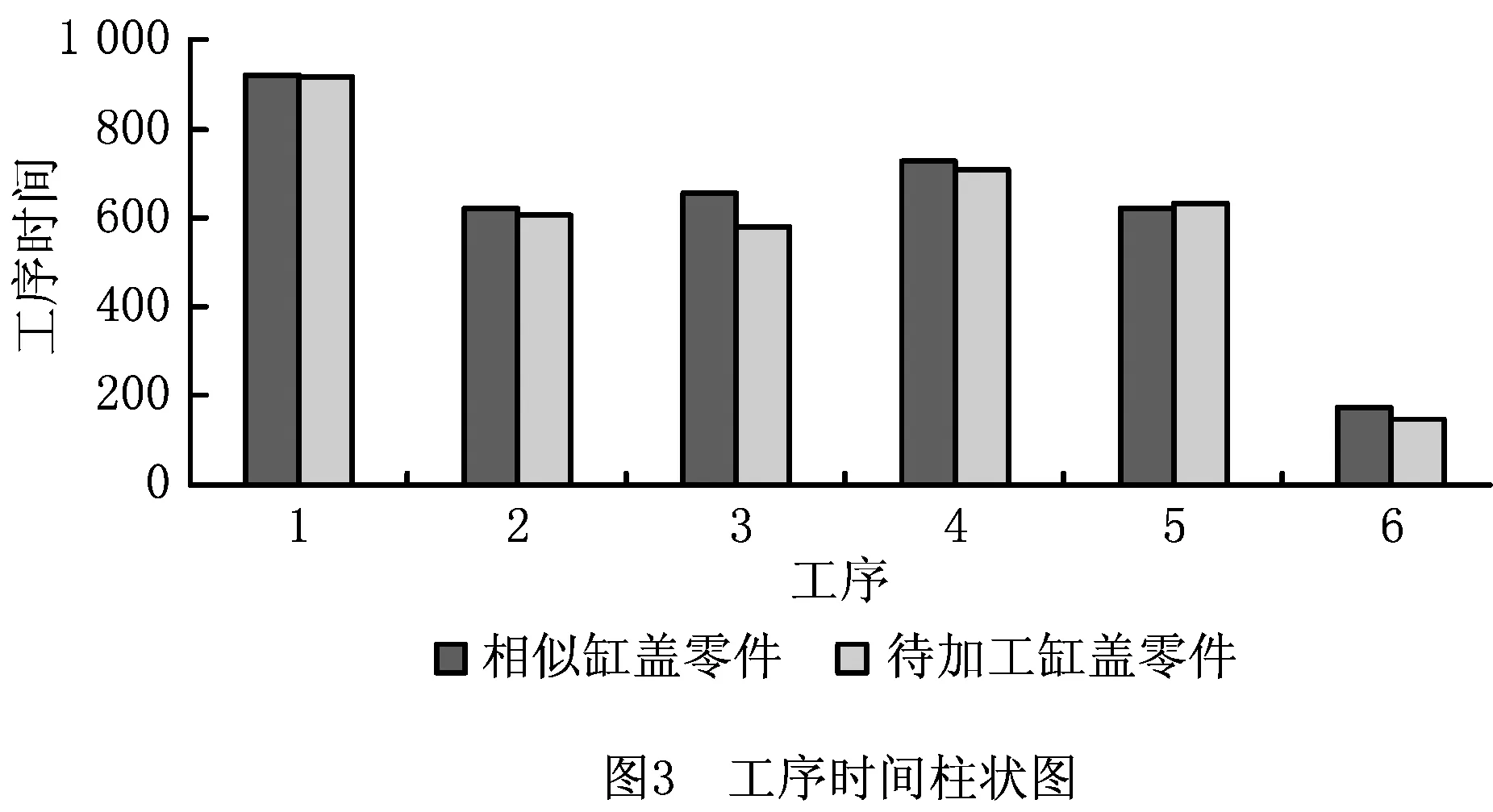
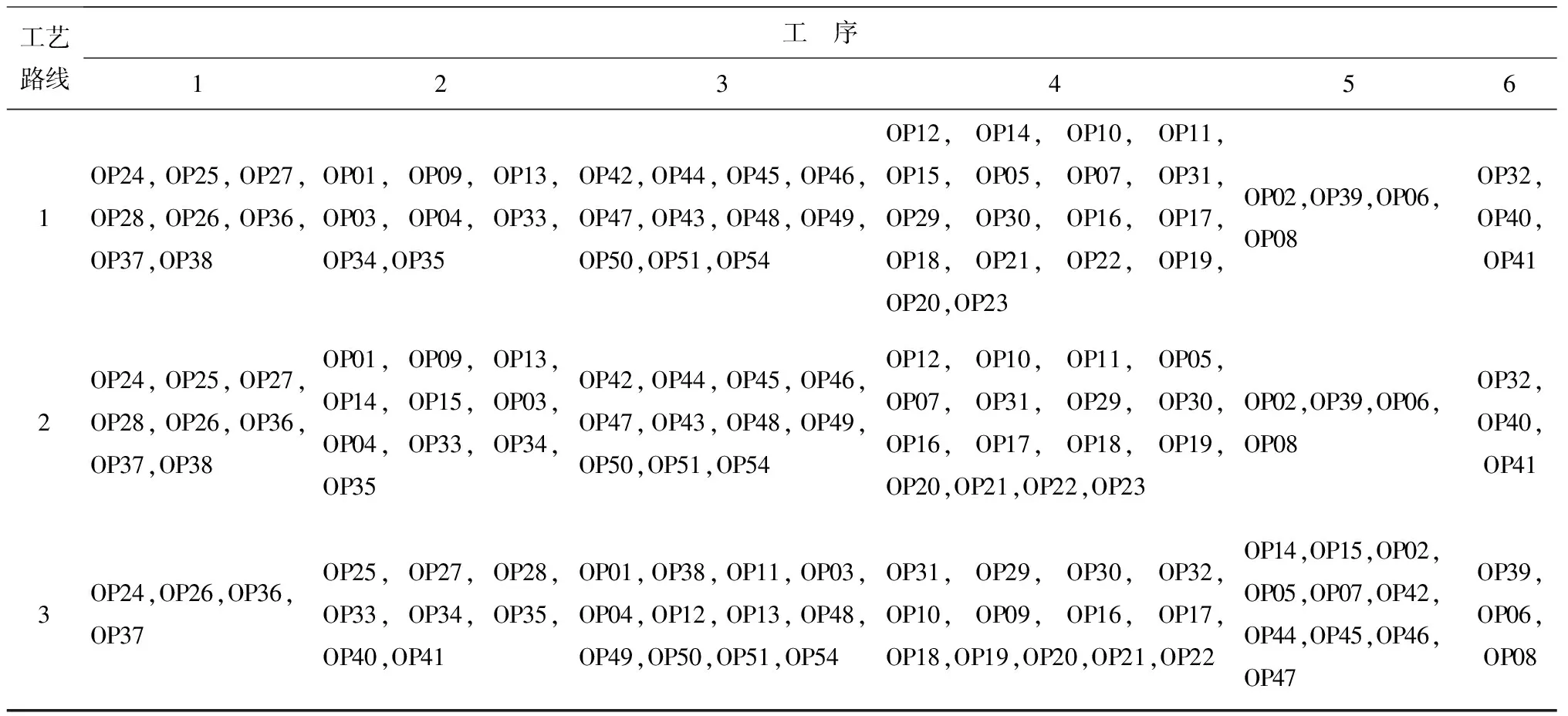
表5 工艺路线信息

工艺路线1的目标函数值为1 312.73 s，此时非切削加工时间为738.35 s，空闲时间为1 887.10 s；工艺路线2的目标函数值为1 323.43 s，其中非切削加工时间为738.35 s，空闲时间为1 908.50 s；当利用模拟退火算法对工艺路线进行重新规划时，只考虑机床的加工能力要求，并没有考虑零件在机床中的装夹约束，导致无法确定机床的定位时间。因此，仅以空闲时间最小作为工艺路线3的目标函数，其值为199.31 s。

模型1可以利用分支定界算法求得工艺路线的局部最优解，而模型2只能利用遗传算法等智能算法求得工艺路线的局部近似最优解，相较于模型2，模型1极大地提升了求解效率和精度。另外，与相似缸盖零件的工艺路线比较，模型1、2保持了基本的工艺流程不变，为90.38%，只是在局部插入若干加工操作。因此，通过简单的调整即可实现新零件工艺路线的规划，适合混流生产或中小批量转产、紧急订单插入等情况。

重新规划工艺路线虽可有效平衡各工序的作业负担，降低空闲时间，实现工序平衡以及工艺路线的全局优化。但此情况下每道工序需要根据分配的加工任务重新设计、安装以及调试夹具，且由于工艺路线较相似缸盖零件工艺路线已完全改变，操作工人需要大量时间和精力重新培训、熟悉每道工序的加工过程，降低了加工操作的可靠性，浪费了大量宝贵的资源和时间，适合大批量生产中转产。

5 结束语

为增强工艺知识重用性，提高工艺规划的柔性和动态适应性，本文提出了基于时间向量和矩阵的多工序加工系统工艺路线重组建模与优化方法。在保证基本工艺流程不变的前提下，通过考虑各工序之间相互关联的加工任务、加工设备、夹具、刀具等信息建立向量形式的工艺重组过程模型，在向量或矩阵中利用简单重复的插入操作即可获取可行的工艺路线。该方法大大降低了工艺路线重组模型的复杂性，提升了求解效率，有利于实现工艺路线的在线实时动态调整，适合混流生产或中小批量转产、紧急订单插入等情况。未来，将结合制造企业的数字化与信息化系统特点，在加工特征识别与零件相似性分析、工艺重组过程的自动化与标准化、可重组工艺规划平台开发等方面进行深入探讨和研究，进一步增强该工艺规划方法的实用性。