基于深度学习的“问题教学”初步实践与运用

吴伊敏

在传统的教学下，教师在讲台上将知识灌输给学生，学生自行探究的时间甚少，即便课堂上安排了小组讨论，也未必能保证每个学生都能深入思考。六年级作为毕业班，需要教授的内容多，时间短，课程安排得总是很紧迫，知识满堂灌的现象更加严重。在东莞市松山湖中心小学刘老师的带领下，我开始接触并了解基于深度学习的“问题教学”模式，在这个教学模式下，教师将课堂还给学生，让每个学生都能深入学习。

一、什么是“问题教学”

“问题教学”是以培养学生的学科核心素养为导向，用“问题清单”来驱动学生的深度思考，学生通过解决教师罗列的“问题清单”，逐步完善他们对知识的认知结构，变碎片化学习为结构化学习，变被动学习为主动学习，变模糊学习为可见学习，生成一种更开放、更灵活、多线分层并进的新的教学结构。

二、运用“问题教学”模式的设计过程

根据“问题教学”模式的4个环节：问题引发——问题探究一一互动建模一一问题解决，设计了人教版六年级下册《圆柱的表面积》这一节课。

在“问题引发”环节，我设计了两个问题：

①你们是怎么制作圆柱的？能不能用自己的语言说一说？

②圆柱表面积指的是什么？是由哪几个面的面积相加呢？

通过这两个问题的梳理，引导学生回顾如何制作圆柱，借助上节课对圆柱的各部分组成的认识，总结出圆柱体表面积是由哪些部分构成的，这对后面学生们独立完成“问题探究”部分做好铺垫。

接着是“问题探究”环节，这个部分我设计了三个问题：

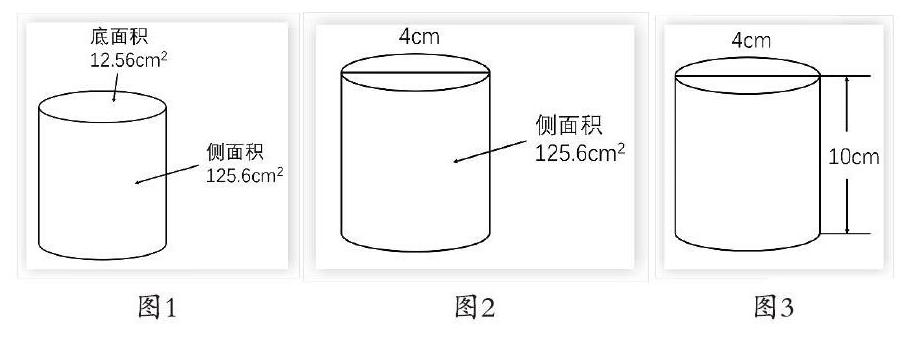
①根据“圆柱的表面积=圆柱的侧面积+两个底面的面积”，你能算一算以下这个圆柱的表面积吗？（写一写））（见图1）

②你能算出底面积后，再算出这个圆柱的表面积吗？（想一想，写一写）（见图2）

③你还能算出这个圆柱的表面积吗？（先想一想，再与同学们讨论，最后写一写）（见图3）

这三个问题的设计浅入深出，首先让学生根据公式计算圆柱的表面积，清楚了解要计算圆柱的表面积需要知道哪几个面的面积。接下来第二个问题增加难度，需要学生根据已有学习经验，计算出圆柱的底面积后，再算圆柱的表面积。最后第三个问题，只给出底面直径和高来计算圆柱的表面积，通过解决上面两个问题，学生已经知道圆柱的表面积是由几个面组成和这些面的特点，所以在解决第三个问题时，学生会想到先分别求侧面积和底面积，再算表面积。这样的设计层层递进，每个问题都在上一个问题的基础上进行探究，降低了難度。

“互动建模”环节，学生要在老师的提问或遍问的引导下，总结出“如何求圆柱侧面积？”“如何求圆柱的底面积？”“如何求圆柱的表面积？”等问题，帮助学生梳理出以下三个知识点：

①圆柱的表面积=圆柱的侧面积+两个底面的面积

②圆柱的底面是一个圆。

③圆柱侧面展开是一个长方形，长=底面周长，宽=圆柱的高。

最后是“问题解决”环节，学生独立完成课本p23练习四1、6，检验学习的知识，巩固圆柱侧面展开前后各部分对应关系和圆柱计算表面积公式。

整个教学过程中，学生手上都会有一份“学习单”，里面呈现了每个环节的内容，学生只需在老师的带领下，按照“学习单”的内容学习即可。

三、运用“问题教学”模式的实践

为了形成对照，我分别在两个班上运用不同的模式上《圆柱的表面积》这一课。六（1）班运用我设计的“问题教学”模式，六（2）班则运用传统教学模式。

运用“问题教学”模式来上课，对老师来说是一个很大的挑战，老师既要控制好全局，还要在“互动建模”环节通过问答带领学生梳理知识。两个班运用不同的模式，用一节课的时间来讲述《圆柱的表面积》后，第二天我运用早读的时间，让两个班同时完成《南方新课堂》第13页的第5题，根据表中给出的已知条件进行计算并填表。

我重点关注最后一列中求表面积的三个填空的正确率。从上往下三个答案，六（1）班正确率分别是81%，76.2%，78.6%。六（2）班正确率分别是75.6%，73.3%，77.8%。从数据上看，六（1）班的正确率与六（2）班的相比，六（1）班稍微领先，但差距不是很大。

这是我第一次使用“问题教学”模式教学，从单次教学效果来看，“问题教学”模式下的正确率虽然只是稍稍领先。但“问题教学”是以问题带领学生的进行知识建构和问题解决的，是将本节课的核心问题用问题串的形式呈现给学生，同时以“学习单”的形式放手让学生去探究。学生在这过程中明确了自己的学习目标，也通过“学习单”的提示清楚地知道达成目标的途径方法，并且有较为充足的时间去独立思考、自主探究，同时也会促进同桌、小组间的协作学习。所以从长期来看， “问题教学”模式是不断带领学生自主学习，深入思考，是非常可取的。