基于小学数学猜想和证明的反例研究

■山东省临沂市莒南县第二小学 董文敏

一、背景

猜想和证明是数学的核心，应成为小学学生数学经验的核心要素之一。在猜想和证明定理的过程中，数学家从事各种活动，这些活动在定理和证明的最终形式中没有明确描述。尤其是，数学家必须不断地测试其数学论证的逻辑链的正确性和连贯性，例如通过搜索反例。实际上，Lakatos 指出“非正式的，准经验的数学不是通过不可否认的定理数目的单调增加，而是通过猜测和批评，通过证明和反驳的逻辑不断地改善猜测”，提出反例的反驳在数学中也经常起重要作用。为了概念化学校数学中的证明概念，Stylianides提出了“知识-诚实原则”，其中“规定学校数学中的证明概念应被概念化，以便对数学作为一门学科诚实并同时尊重学生作为数学学习者”。根据对证明的概念化，他进一步分析了一个课堂情节，三年级学生试图证明两个奇数之和是偶数。正如他提到的那样，“诚实守信”原则可以在概念化学校数学中的其他概念时使用，也可以更广泛地使用它，该原理不论是对学校数学中的证明还是对所有数学都非常有用。这项研究的目的是考验数学教师和教育者如何在小学阶段实现数学学习，而这在数学上是诚实的，并带有证明和反驳。本文的重点是小学生是否有可能体验真正的数学活动，特别是证明和反驳，作者将描述和分析两个5年级儿童在提出反例时的反应，这是一种基本方法，在他们的问题解决过程中提出了反驳。

二、小学数学思想

（一）研究对象

本文的主要重点是学生的数学活动，以及在小学数学中的反例。作者对一对在日本公立小学就读的五年级生Daiki和Takuya（化名）进行了采访。访谈是在日本进行的一项较大研究的组成部分之一，作者一直在探索如何促进学生在数学探究中使用动作证明。选择Daiki和Takuya参加访谈的主要原因是，据他们在另一所公立小学当教师的父母说，作者之间的关系十分融洽并可以清楚地表达彼此的想法。父母期望学校提供丰富的话语数据来分析孩子的思维，而作者和孩子在面试前的简短交谈证实了这一点。根据他们的成绩单和父母的评论，他们的数学能力可以被判断为Daiki（优秀）和Takuya（平均），但是他们的能力并不是选择他们作为参与者的重要因素。

（二）研究方法

访谈中的任务与“两位整数和其位数与原始整数的顺序相反的整数之和”有关，例如32+23=55（以下简称“两位整数之和”）。日本学生通常会在八年级时遇到此任务，他们希望通过代数论证证明两个整数的和是11的倍数。但是，我决定在本次采访中使用此任务，因为大多数小学生倾向于猜测更原始的语句，例如“当两个整数的和仍然是两位数字时，和的十位数和一位数相等”（例如，32+23=55，5=5）; 这种趋势将使作者更容易提出反例（例如85+58）并观察学生的反应。面对反例之后，学生还可以体验将他们的原始猜想改进为更全面的猜想，即两个整数的和是11的倍数。采访大约花了50分钟，是半结构化的：首先，作者将任务提交给Daiki 和Takuya，然后他们做出了上述原始猜想并试图证明这一点，然后反例“85+58？”被提出来使他们改变了他们的第一个猜想。为了在猜想和证明之后提出反例，作者故意显示了只有两个整数的和在早期阶段仍保持两位数的情况（52+25、26+62和31+13）。

如上所述，这项研究是作者对动作证明的研究的一部分，因此要求Daiki和Takuya利用操纵对象证明其猜想。采访准备了两种类型的操纵对象：一个是日本的100 日元，10 日元和1 日元硬币，另一个是黄色，绿色和红色柜台。在采访中，Daiki 和Takuya能够选择他们想要使用的操纵对象。在采访中，Dai⁃ki 和Takuya 可以使用工作表，操作对象以及一支铅笔，并且他们被要求对操作对象进行检查，但不是单独而是协作进行，因为希望他们在这种情况下更自然地表达自己的思想。环境及其表达方式似乎有助于分析其思想。采访被记录并抄录；还使用摄像机记录了他们与操纵对象的数学活动，交流和“动作”。通过视频记录和他们在工作表上写的内容分析成绩单，重点是他们证明自己的原始猜想，面对反例，然后重新检查该猜想和证明的过程。

三、研究结果

（一）证明原始猜想

Daiki 和 Takuya 计算出了 52+25=77、26+62=88和31+13=44，并对计算结果感到惊讶。然后，他们做出了各种推测，其中，他们试图通过使用以下计数器来证明“两个整数之和的十位数和一位数相等”。

首先，他们认为绿色柜台和红色柜台分别为10和1。Daiki 和Takuya 然后选择了71+17 作为两个整数和的示例，并将其表示为图1的状态1。注意到他们的小错误后，他们移走了两个绿色柜台。然后，他们将71 的七个绿色计数器移动到17 的七个红色计数器的一侧（状态2）。接下来，他们将17 的绿色计数器和71 的红色计数器（状态3）拿走，并将它们放在七个绿色和红色计数器上方（状态4）。然后，他们确认柜台的布置代表88，如下图所示：

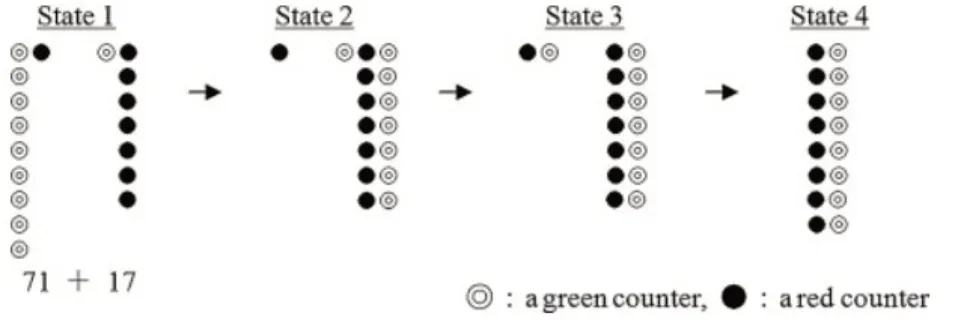
图1 在71+17中重新安排的过程

（二）面对反例修改猜想证明

在标记了数字A 和B 之后，Daiki 提到了两个事实。A 的十位数和B 的十位数相同；B 的十位数和A的十位数也相同。然后，他说由于每个和的十位数和个位数相等（在71+17、70+7=77 和7=7；1+10=11和1=1的情况下），因此十位数和个位数两个和的和的位数也相等（77+11=88和8=8）。他们确认可以将相同的想法应用于85+58，如下图所示：

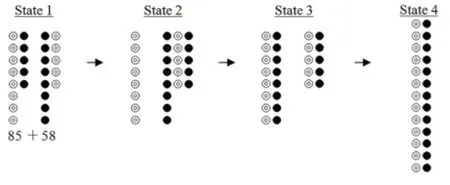
图2 在85+58中重新安排的过程

四、结语

这项研究表明，只要安排了适当的环境（在这项研究中，与两个整数的和和动作证明有关的任务），即使在小学阶段，也有可能获得这种数学学习，并且接受反例为了体验真正的数学过程，承认猜想的虚假性以及更深入地分析猜想和证明很重要。因此，对于不仅在小学而且在所有年级的教学都具有意义，教师应准备适当的学习环境，并在面对反例时向学生提出以下问题：例如，“您的猜想为什么会变成假？”“在反例的情况下，您的证据中有哪些部分会分解？”“在反例的情况下，您的证明的哪一部分可以适用”和“您是否可以利用这一部分来发明一个新的猜想？”。