基于消费者损失效用的概率销售策略研究
杨 光,刘新旺,秦晋栋
(1.南京信息工程大学管理工程学院, 江苏 南京 210044;2.东南大学经济管理学院,江苏 南京 211189;3.武汉理工大学管理学院,湖北 武汉 430070)
1 引言
近年来随着互联网支付平台的兴起,消费者的消费方式发生了巨大的变化,现代市场行情变得更为错综复杂,市场竞争异常激烈,任何企业要想成功进入、占领、巩固和扩展市场,采用正确的营销策略显得尤为重要。一般来讲,销售商可供选择的市场营销策略包括产品策略、价格策略、促销策略和渠道策略等等[1],其中促销策略最为常见,促销手段主要有折扣、返现、抽奖以及免费体验等方式,促销形式包括广告宣传、公共关系、促销活动、人员销售、口碑操作等,而概率销售作为促销策略中比较新颖的策略越来越被人们所熟知。2008年Fay和Xie首次提出了概率产品(简称PG)(Probabilistic Goods)和概率销售 (Probabilistic Selling)(简称PS)的概念[2],概率销售作为一种新型销售模式与其他销售方式相比有其独具的特点和明显的优势,能够达到扩大市场、细分市场、差异化定价、弱化市场不确定确定影响、平衡供求、增加资源利用效率等效果[2]。
关于概率销售领域的早期文献主要关注垄断与竞争[2-5],需求不确定[2,5]等主题。最近的概率销售文献主要关注以下几个主题,一是将库存管理理论用于概率销售策略的研究[6-9],Fay和Xie[7]研究了产品时间分配对概率商品消费者的影响。PS作为一个库存管理机制既能提高销售商或厂商利润又能增加社会福利; 二是与概率销售策略相似策略的比较分析[10-12],Chen等[11]考虑一个两阶段模型来研究报价(PP)与自己标价(NYOP)两种不同销售机制的影响。三是将博弈方法及动态规划等用于概率销售的研究[9,13],Xiao Yongbo和Chen Jian[9]用连续时间离散状态有限期限动态规划模型,研究了两种场景下的最优决策,其价值函数可以作为基准来评估概率销售(PS)关于需求的诱导效应和稀释效应;Cai Gangshu等[13]利用静态博弈研究两个供应商和一个销售商如何使用概率销售和渠道选择问题;Rice等[12]模型将概率销售与削价销售策略进行了比较分析,模型显示概率销售与削价销售相比具有提高边际收益和库存利用率等优势。
与概率销售密切相关的主题是考虑消费者理性对概率销售的影响[14], 以及销售商如何利用产品属性差异来创造概率产品[2,7-8]及在竞争市场下概率销售策略的实践应用[4-5,15],Fay等[10]研究表明概率销售影响零售商实施概率产品的类型和数量,采用PS策略可以改变最优产品的数量,还可以作为新产品的替代或补充。Huang Tingliang和Yu Yimin[14]研究表明概率销售在有限理性条件下最优,可以减少厂商间的价格竞争及增加产业利润,研究指出人们低估了概率销售对有限理性消费者的作用。值得一提的是很少有研究者利用不同质量产品来构造概率产品。Zhang等[8]研究不同质量市场下的概率销售策略,研究发现如果销售商产能过剩则销售商在不同质量市场下采取概率销售是有利可图的。
上述文献没有考虑消费者的损失偏好,由于消费者的需求个性越来越分散化,许多文献关注消费者的损失厌恶或损失规避。Zhao和Stecke[16]考虑了消费者的损失厌恶对提前订购策略的影响并研究了销售商提前销售的利益最大化问题。Abdellaoui等[17]提出多种损失厌恶的概念并证明多数个体存在损失厌恶。Blavatskyy[18]将损失规避的概念扩展为更一般的情形,即损失规避的结果不是用钱去度量,研究表明人们可能会倾向于模糊偏好来代替博彩。借鉴前景理论中的参考点依赖和风险损失规避效应,Won[19]分析了消费者的损失厌恶对经验优势的影响。Kim和Lee[20]介绍了在消费者损失厌恶下的销售商利益最大化行为决策,并讨论了损失厌恶在价格歧视和产品差异中的实践应用。Wang和Webster[21]将损失厌恶引入报童模型中考虑单周期的报童决策问题,研究发现在损失厌恶条件下如果不存在缺货成本,报童的订购量会多于风险中性条件下的订货量。将消费者分为损失中立型和损失厌恶型,Ma Shanshan等[22]考虑实体渠道和网络渠道两种销售渠道,研究了销售商是否应该参与网上渠道销售,并检验了消费者的需求均值对销售者策略的影响。最近,杜文意等[23]在损失厌恶型零售商存在资金短缺的现实情形下,研究了基于融资需求的损失厌恶型零售商订货策略问题,王良等[24]对静态线性损失厌恶下的最优资产配置策略模型及其性质进行了分析,构建了基于TGARCH-EVTPOT-GPD的动态市场风险测度方法,提出了时变损失厌恶条件下基于动态条件风险约束的ETF基金最优资产配置策略模型。
虽然上述文献主要关注不同情境下的概率销售策略,但大多研究者忽视了消费者在购买概率产品后会产生潜在损失。概率产品被认为是一种“随机产品”,只有在购买后产品的信息才会被披露,若消费者购买后的概率产品是低质量产品,则消费者不准退货,这被称为“不返还”策略。在实际的销售实践中存在以下两种可能购买后悔损失情形:(1)消费者不应该购买任何产品;(2)消费者应该购买最偏爱的透明产品。第一种被认为是“购买损失”,第二种被认为是“选择损失”。
本文主要的创新点体现在以下几个方面:一是我们构建了概率销售在损失中性和损失厌恶下异质产品的概率销售模型并探讨期望损失对概率销售策略的影响和作用。二是我们模型纳入了异质产品市场下的概率销售的一些重要特征,工业实践表明生产高质量产品的厂商一般不会采用概率销售策略,因为销售价格打折的概率产品会让他们名誉受损。
三是我们首次将期望损失纳入概率销售模型中,研究表明消费者的期望损失能否激发销售商采用概率销售策略主要取决于消费者对购买损失和选择损失敏感度。“购买损失”会使得概率产品的感知质量与质量正相关,而“选择损失”则会让感知质量与质量负相关,我们把后者称为“反质量歧视”。当消费者对“选择损失”更敏感时,则概率销售的零售商会利用“反质量歧视”,此时对于高端消费者来说,期望损失会在更大程度上降低概率产品的感知质量,这种“反质量歧视”可以增加消费者对产品的感知差异,并保持概率产品对两端消费者的吸引力。
最后我们比较销售商在损失中性和损失厌恶下的概率销售策略变化和对收益的影响,同时验证了异质产品市场下 “反质量歧视”效应和实施概率销售中的“不返还”策略,这些机制可以扩大产品间的质量差异,同时让销售商获取更多利润。
2 基于损失效用的概率销售模型
2.1 问题描述
2008年Fay和Xie[2]首次提出了概率产品和概率销售的概念,概率产品并不是一个具体的产品, 而是指销售商通过概率的指定在一系列销售的产品中创造出的虚拟产品。概率销售是指一种销售策略,即销售者利用其现有的产品或服务来创造概率产品,并把概率产品作为对潜在购买者的一种附加购买选择。例如一般国外消费者愿意从网站Hotwire.com或Priceline.com购买带折扣的酒店,而带折扣酒店的信息在消费者购买后才被披露,这种销售商销售策略即为概率销售策略,这种产品为不透明产品或概率产品,而传统实体销售的产品在后文中称为透明产品,再例如销售商在传统销售模式下以原价销售两种产品A和B,而概率销售模式则以折扣价格销售概率产品(PG),此时产品类型只有在购买后才能被披露,具体销售模式见图1所示。

图1 传统销售与概率销售对比图
2.2 假设说明
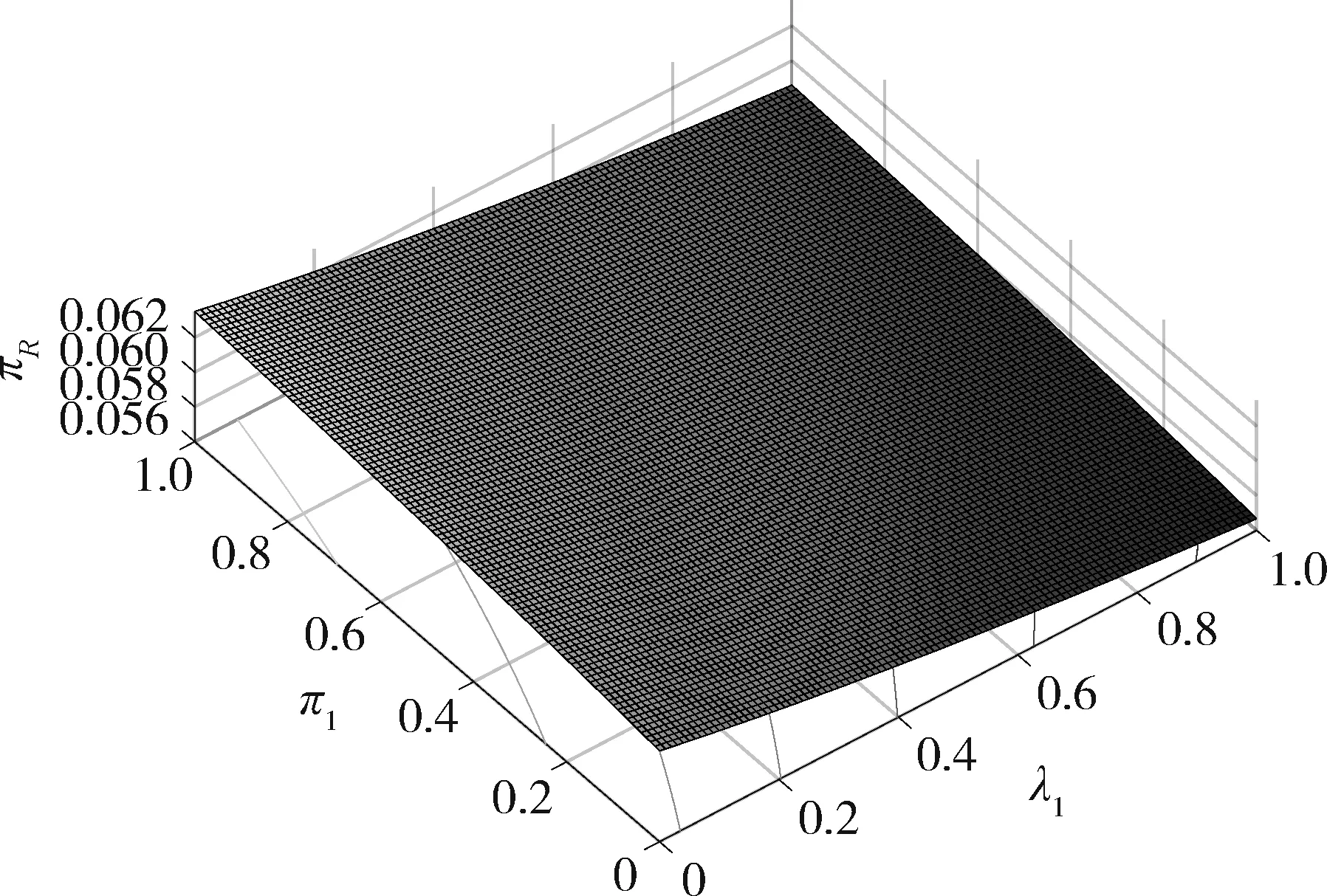
假设整个市场有两个销售商,销售商H和销售商R,每个销售商仅销售单位产品,销售商H提供质量等级为qH的透明产品,而销售商R提供三种不同产品,第一种是质量为qM的透明产品M,第二种是质量为qL的透明产品L,第三种是由产品M和产品L混合的概率产品R,消费者自主选择产品而购买产品的质量等级则随机产生,购买到产品的质量等级只有两种qM或qL,其中qL< 假设市场中存在大量单位需求消费者,每个消费者只购买一个产品,考虑本文模型计算的复杂性假设消费者的质量偏好服从均匀分布,即θ~U(0,1),质量偏好为θ的消费者在损失中性下以价格为pi购买产品i(i=H,M,L)的效用为u=θqi-pi(i=H,M,L,R)。 定义不同损失偏好下消费者的效用[16]为, u 上述效用区分了损失中性消费者和损失厌恶型消费者,消费者购买透明产品不存在损失,因为消费者购买透明产品不存在不确定性,而购买概率产品,由于产品质量的不确定性导致消费者购买后损失。下节将分别讨论损失中性和损失厌恶下的概率销售模型。 为了便于与损失厌恶下的概率销售模型相比较,首先我们研究在损失中性下的概率销售模型,将损失中性概率销售模型作为基准模型,采用逆向演绎方法,从最后一阶段消费者选择产品开始分析,给定价格和质量水平(pi,qi)(i=R,H),我们得到不同消费者偏好对质量的临界点:第一个临界点是消费者买概率产品和不买产品无差异,第二个临界点是消费者买产品H和买产品R无差异,上述两个临界点如下: (1) 销售商R和销售商H的需求分别为(θR-θ0)和(1-θR),因而销售商H和销售商R的利润分别为 πR=pR(θR-θ0),πH=pH(1-θR) (2) 根据式(2)可以求出均衡价格和质量,在第一阶段销售商R在区间[1,qM]上选择最优质量,得到下面损失中性下的性质: 引理1 如果消费者购买概率产品R中获得产品M没有损失,则应满足下列条件: θqM-pR≥max{0,θqH-pH} 证明:见附录引理1的证明。 在引理1的基础上我们得到下列损失中性下的结论。 定理1(损失中性)在损失中性下有下列结论: 证明:见附录定理1的证明。 本节首先定义期望损失和感知质量,类似损失中性情况,我们建立基于损失厌恶下的概率销售模型,进而得到一些性质。 定义1 期望损失 (3) 其中λi(i=0,1)分别表示消费者买产品和不购买产品H两种类型损失厌恶下的损失厌恶系数,[x]+=max{0,x}。 由上述定义1说明当消费者购买概率产品买到产品L时会损失厌恶,这是消费者理性选择的结果,当消费者购买概率产品后得知是产品M不会损失厌恶,因为消费者在购买前清楚购买概率产品的最好结果就是买到产品M, 期望损失分为存在下列两种类型: (1)购买行为本身的损失(不买与买到低质量产品作比较),比如消费者购买概率产品买到低质量产品,则消费者可能会想如果不买概率产品则不会有损失,此种类型被认为“购买损失”。 (2)不购买透明产品带来的损失(买透明H产品与买到低质量产品作比较),例如购买概率产品买到低质量产品,消费者可能会想如果去选择透明产品则不会有损失,此种类型被认为“选择损失”。 定义1考虑上述两种类型的损失厌恶,其中λ0是类型(1)的损失厌恶系数,λ1是表示类型(2)的损失厌恶系数,这两个类型的损失厌恶系数在后文中将起到关键的作用。 根据式(3),期望损失的第一项为正当且仅当θ (4) 当然可能存在θ1 (5) 我们定义概率产品的感知质量: 定义2 感知质量 根据感知质量的定义,则存在下列两种情形: 图2 当θ1≥pR时感知质量的倒U形曲线 图3 当θ1 引理2 消费者的对产品R的感知质量是呈倒U/V型,存在下列两种情形: 其中θ1和θ2分别如式(2)和(4)所示。 (6) 当消费者购买概率产品和买高质量产品无差异的质量临界点由 (7) 引理3 消费者分类(损失中性) 质量偏好位于区间θ∈[θ0,θR]上的消费者会选择概率销售产品R,质量偏好位于区间θ∈[θR,1]上的消费者会选择产品H,θ0和θR如式(1)所示。 引理4 消费者分类(损失厌恶) 质量偏好位于区间θ∈[ϑ0,ϑR]上的消费者会选择概率销售产品R,质量偏好位于区间θ∈[ϑR,1]上的消费者会选择产品H,ϑ0和ϑR分别如式(6)和(7)所示。引理4说明当消费者对质量要求比较高θ∈[ϑR,1]时,会选择产品H,当消费者对产品的要求比较适中θ∈[ϑ0,ϑR]时,会选择概率产品,当消费者对质量要求比较低θ∈[0,ϑ0]时离开市场不购买任何产品。 由引理4知,在损失厌恶下销售商R和销售商H的利润分别为 销售商R选择pR最大化其利润,销售商H先择pH最大化其利润,解得最优的价格,最优价格均是qR和qM的函数,销售商R再选择最优的qM,得到下列定理2归纳的均衡结果: 定理2(损失厌恶) 在损失厌恶下有下列结论: (3)γ1(λ1)和γ2(λ1)均是关于λ1的递增函数,销售商R的最优利润与损失中性最优利润相比有下列特点: 证明:见附录定理2的证明。 定理2说明以下问题,第一,当存在损失厌恶的情况下,只要λ0足够小(与λ1相比),λ0小于特定的阀值时λ0是关于λ1的递增函数,此时销售商R提供概率产品,事实上若消费者在购买概率产品后有损失,则概率销售策略此时不具有吸引力,致使消费者不愿意购买概率产品,但下面的情形则消费者愿意购买概率产品,当λ1>λ0时,存在下列几种情况,第一种情况λ0≤γ1(λ1),与定理1中的情况(1)不同,此时销售商总是采用概率销售策略,第二种情况与定理1中的情况(2)相同,当γ2(λ1)≥λ1≥λ0时销售商也总是采用概率销售策略,与定理1相比在λ1>λ0时销售商R似乎更愿意采用概率销售策略;而相反在λ1≤λ0时也存在下列三种情况,第一种情况γ1(λ1)≤λ1≤λ0时,销售商R不采用概率销售策略,这与定理1的情况(1)相同,第二种情况与定理1的情况(2)类似,只有当λ0≤γ2(λ1)时销售商才开始采用概率销售策略,与定理1相比,销售商R在λ1≤λ0时不太倾向使用概率销售策略。 第二,当且仅当消费者买产品H的损失厌恶系数比不买产品H的损失厌恶系数小时(例如λ1≥λ0),销售商R的利润比在损失中性下利润高,由引理2知消费者的感知质量呈倒U/V形,因此使用概率销售策略会更容易让分布在两端的消费者受损失,即对质量要求低的消费者会因为购买产品H而损失,而对质量要求高的消费者会因为不购买产品H而损失,前者的损失受厌恶系数λ0影响,而后者则受厌恶系数λ1影响,λ0作为购买损失类型(1)的度量,消费者也是通过λ0来感知产品质量的,随着消费者对质量的要求越来越高,对产品质量的感知能力也越来越强,若消费者感知到产品质量越来越差时,则此时消费者便不愿意购买,这就迫使销售商为了留住消费者而降价进而导致销售商利润降低;λ1作为损失类型(2)的一种度量,随着消费者对质量要求越来越低,对产品质量的感知能力也逐渐降低,我们称这种规律为“反质量歧视”,两销售商对高端消费者(θ∈[max(θ1,θ2),1])的争夺竞争激烈,消费者对概率产品的感知质量的削弱会增大概率产品和透明产品之间的差异,这就致使销售商增大质量差异定更高的价格,进而使得概率销售商获取更高的利润,具有损失厌恶的概率销售和损失中性的概率销售的利润谁高谁低取决于两种损失厌恶类型消费者的期望损失敏感性的强弱。 定义 其中γ1(λ1)和γ2(λ1)的表达式见附录定理2的证明。 从定理2知当固定λ1不变时,随着λ0增加到阀值γ1(λ1)时,销售商R停止概率销售。下面讨论当固定λ0不变时,随着λ1增加会出现什么规律?下面的推论给出了回答。 推论2 (极限性质)γ(λ1)关于λ1递增,对任意的λ0≥0,存在反函数 若λ1≤γ-1(λ0),则销售商只销售透明产品,否则销售商R只销售概率产品。另外,存在下列极限性质: 证明:见附录推论2的证明。 推论2说明保持λ0不变,即使损失厌恶系数λ1趋向无穷大,销售商R仍然销售概率产品,这是因为实施“反质量歧视”的唯一方法就是采用概率销售,随着λ1的逐渐增大,销售商会降低产品L在概率产品中的比例,但这个比例不会降到0,这就意味着消费者在买概率产品时买到产品L的几率会降低,在存在市场竞争下销售概率产品可以降低消费者对产品的感知质量,换句话说销售概率产品可以有效降低两销售商之间的竞争,因为竞争情形下当产品的质量差异不大时消费者会夸大市场中的产品的感知质量差异。 本节主要探讨参数对不同损失情形下最优收益、最优质量、价格及需求的影响,由定理2知销售商R的利润函数关于λ1递增,关于λ0递减,下面我们进一步研究参数λ1和λ0对产品R的期望质量的影响,固定qM和λ1不变,增加λ1会减少低端消费者对概率产品R的需求,因此销售商R必须降低价格增大qM,这会加剧销售商R和销售商H之间的竞争,两个销售商的利润均会降低。 首先固定qH,qM研究qM和λ0及λ1的关系,图4和图5分别是当qH=3,qM=2及qH=1.5,qM=1.2时销售商R的qM和λ0及λ1的关系图,由图4和图5知当λ0≥γ(λ1)时,销售商R不会销售概率产品,故随着λ0的增大,qM增加到qM或者降低到qL,主要取决于利润大的产品。 图4 qR与λ关系当qH=3, qM=2 图5 qR与λ关系当qH=1.5, qM=1.2 下面我们研究销售商R及H随着参数λ1和λ0的变化关系,下列推论3揭示他们之间的关系。 推论3 固定λ1,销售商R和销售商H的价格、需求以及利润均是关于λ0的递减函数;固定λ0,销售商R和销售商H的价格、需求以及利润均是关于λ1的递增函数。 证明:见附录推论3的证明。 推论3说明固定λ1,则销售商R和销售商H的收益均随着λ0的增大而递减,下面我们结合图6-10来说明,具体参数设置如下qH=3,qM=2,qR=1.5,图6说明销售商R的利润随着λ0的增大而递减,随着λ1的增大而递增,图7说明销售商H利润表现出同样的规律,即随着λ0的增大而递减,随着λ1的增大而递增。固定qH=3,qM=2,图8说明销售商R的定价随着λ0的增大而递减,随着λ1的增大而递增,同理图9是销售商H的定价随厌恶系数(λ0,λ1)的变化关系,图9说明销售商H的最优价格关于λ0递减而关于λ1递增,与销售商R的定价(图8所示)相比销售商H的定价随着λ0递减得更快,其中销售商R的定价随着λ1直线增长,而销售商H的定价随着λ1曲线增长,图10和图11是销售商R和H的需求随着厌恶系数(λ0,λ1)的变化关系,图10和图11说明销售商R和H的需求均关于λ0递减而关于λ1递增,同时销售商H的需求是销售商R需求的两倍。 图6 销售商R的利润随λ0和λ1的变化关系 图7 销售商H的利润随λ0和λ1的变化关系 图8 pR 随λ0和λ1的变化关系 图10 DR 随λ0和λ1的变化关系 图11 DH随λ0和λ1的变化关系 本文首先构建了损失中性下异质产品的概率销售模型,以此为基础建立了损失厌恶下异质产品的概率销售模型,研究了不同损失类型消费者对异质产品概率销售策略的影响,最后讨论了相关参数对销售商的收益、定价、最优质量的影响。 概率销售作为一种新型的销售模式,本文主要解决了在销售期限内如何控制概率销售中产品质量差异问题,消费者的损失偏好如何影响收益、定价和需求的问题,销售商在面对不同类型损失的消费者,控制产品的质量,将概率销售和普通销售有机结合起来,对于高档产品的销售商主要采用普通销售,主要吸引高端消费者,扩大产品的差异化程度实行差异化定价;对于中低档产品的销售商采用概率销售和普通销售相结合的策略,当产品的质量适中时采用概率销售,当产品的质量差异位于两端时则采用普通销售,在具体销售实践中将概率销售和普通销售灵活统一起来,根据消费者的损失偏好灵活控制产品差异,实现最大化收益。对于不同损失偏好的消费者来说,增强对产品质量的感知能力,判断产品的质量,根据自己的判断选择不同的销售商,若消费者对产品的质量要求高,则选择高端产品的销售商;若消费者对产品的质量要求适中,则选择概率销售的销售商,消费者首先应理性判断产品质量,同时兼顾自身的经济状况选择合适的销售商及产品。销售商提供概率销售策略为消费者买到物美价廉的产品提供了一种可能。2.3 损失中性下的概率销售模型
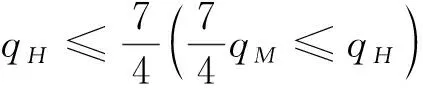

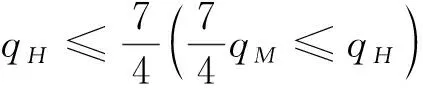



2.4 基于损失厌恶的概率销售模型



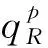












3 数值分析






4 结语

