不确定需求下考虑供应商参与机制的应急资源配置鲁棒优化研究
张梦玲,王 晶,黄 钧
(1.北京工商大学商学院,北京 100048; 2.中国科学院大学工程科学学院,北京 100049)
1 引言
近年来,大规模地震灾害频繁发生,造成了严重的人员伤亡和财产损失。如2008年的汶川大地震,2010年的青海玉树地震,2013年的四川雅安地震,2017年的九寨沟地震。地震灾害发生具有不确定性、动态性、复杂性等特征,使得灾害发生后应急救援过程应急资源需求具有不确定性、紧迫性、持续时间长、需求量大等特点,应急资源保障体系的建是高效救援工作展开的关键。许多学者对应急资源优化配置问题开展研究,早期针对确定性条件下应急资源配置研究,主要有张铱莹[1]为合理解决应急系统管理中的应急资源选址和配置问题,实现应急资源优化管理,构建基于应急系统综合可靠性的多目标应急服务设施选址和资源配置模型。许建国等[2]考虑需求点需求量发生变化时,调整被选择的地址点所需放置的应急物资资源量,使得需求变化周期内需求点被满足的需求总量最大化。Roni等[3]在考虑常规需求和应急需求下,研究了混合库存管理策略问题,以期在现有的政策下得出最优的库存量。对于不确定条件下的应急资源配置研究,主要有:Chen Jingxian等[4]考虑了不确定应急资源需求条件下社会捐赠和救灾机构应急资源购买量,构建了一个带有报童方法的应急资源库存-运输的两阶段模型。Rawls和Turnquist[5]在不确定条件下,利用应急资源的预定位策略考虑了不同类型的设施选址和库存,并建立了相应的两阶段随机规划模型。张玲等[6]考虑灾害发生时需求的不确定性条件,基于灾难情景建立了随机规划模型对应急物资供应中心选址与应急资源配置数量问题进行了研究。葛洪磊和刘南[7]基于复杂灾害情景,分析了应急设施的定位决策、应急物资的库存决策和不同灾害情景下应急物资分配预案问题,建立了相应的两阶段随机规划模型。Ni Wenjun等[8]在不确定需求、预定位库存比例和路网能力下,以救灾过程中剥夺成本最小为目标,提出了最小-最大鲁棒优化模型。Bozorgiamiri等[9]在灾害准备和应对阶段,提出了需求、供应量、采购成本和运输成本不确定条件下救灾物流的多目标鲁棒随机规划模型。
目前商业物流研究中考虑供应商的问题较多,主要研究订货提前期、数量折扣、生产能力、价格折扣、运输时间和服务水平等相关因素对供应商选择和采购策略制定的影响[10-13]。应急资源保障体系中供应商参与的研究主要集中于灾后从供应商紧急采购应急资源和生产能力储备。胡少龙等[14]引入供应商生产能力差异,考虑受灾点需求不确定性,建立基于情景的两阶段随机规划模型解决灾后应急资源采购方案。王珂和吴丽瑶[15]考虑不确定需求条件下,研究实物储备量和生产能力储备量最优储备方案的协调性问题。张自立等[16]考虑企业生产能力,进行了政府补贴对协议企业生产能力储备影响以及政府对协议企业补贴的最优状态的研究。Balcik和Ak[17]基于救灾机构和供应商签订的框架协议来应对突发灾害情况,提出了由供应商生产能力满足受灾点需求的应急资源采购策略,以期望采购成本和协议成本最小化为目标,建立了灾后基于情景的随机规划模型。
早期的应急资源保障策略研究中,主要考虑政府应急资源储备仓库选址与配置的问题,忽视了供应商参与对于应急资源保障效率提升与应急储备成本降低的作用;而在考虑供应商参与的相关研究中,将供应商生产能力储备的引入灾后救灾处置过程的较多,忽视了供应商的整体布局以及供应商生产能力保障与政府储备之间的协调关系。Hu和Dong[18]基于概率情景研究备灾阶段供应商选择问题与灾后应急资源保障策略,但没有考虑震后应急资源需求具有分时段的特点,以及在满足保障效率前提下协调灾前与灾后储备量以降低保障成本。同时关于应急资源需求的不确定性问题大多是研究基于概率分布给出应急需求情景建立随机优化模型,对于地震等大规模灾难的分时段需求其情景概率往往是难以估计的,部分学者运用L1范数[19-20]构建不确定性集合描述不确定条件下的不确定性因素。
本文针对应急资源配置问题,相较于传统的政府储备规划,借鉴商业物流中供应商的采购策略,引入了供应商参与机制的应急资源保障策略,在灾前通过选择供应商建立政府与供应商的合作机制,完成政府储备仓库的选址与资源配置;地震发生后依托政府储备仓库和供应商共同满足救援时对应急资源的分时段需求。针对灾后应急资源具有分时段不确定性的特点,本文引入了L1范式的需求不确定性集合,建立了不确定需求下考虑供应商参与备灾、救援全过程的两阶段应急资源配置鲁棒优化模型,并给出了鲁棒模型的对应问题转换方法,算例仿真验证了模型有效性。本文重点解决不确定需求下供应商灾前、灾后全过程参与机制下的应急资源配置决策问题,以期建立具有全局性、经济性、可靠性、均衡性的应急资源保障体系,提高震后应急救援的效果。
2 模型建立
2.1 问题描述
应急资源保障体系建设由应急物资实物储备与供应商生产能力储备两部分组成,在灾前选择供应商建立政府与供应商的合作机制,完成政府储备仓库的选址与资源配置,突发事件发生后依托政府储备仓库和供应商生产能力共同满足救援时对应急物资的分时段需求,以实现应急救援保障体系建设成本的最优。
备灾阶段合理选择政府储备仓库同时采购应急物资,此时,采购价格与订购量有关,订购量越大,单位应急物资采购价格越低。因此,若政府批量采购应急物资,则能降低单位物资的采购成本;同时若政府采购过量应急物资,则增加了库存与维护成本。地震发生后,需要尽快将政府储备仓库的应急物资运往受灾点,以满足第一时段的应急物资需求,若政府储备仓库应急物资不够时,则要依托协议供应商开始紧急生产应急物资,此时,采购价格和订货提前期有关,订货提前期越短采购价格越高。本文将灾前订购量与灾后订货提前期对于采购价格的关系如图1所示。供应商参与贯穿于地震备灾与救援全过程,若灾前政府采购应急物资较多,则政府储备及维护成本增加;若震后紧急采购供应商生产能力应急物资较多,则政府采购成本增加。因此,应在满足应急物资分时段需求的前提下,合理平衡灾前实物采购与灾后生产能力采购的比例,在保障救援效率的同时降低应急资源保障体系的成本。
本文主要从灾前、灾后两个阶段出发,研究不确定需求下考虑供应商参与机制的应急资源配置鲁棒优化问题,应急物资供应商保障策略如图2所示。第一阶段,即备灾阶段,完成供应商选择和政府储备仓库选址,从供应商处采购应急物资并运往政府储备仓库;第二阶段,即救援阶段,地震发生后,供应商开始紧急生产应急物资。此时,满足受灾点需求的应急物资,一方面来自灾前政府储备仓库的库存,另一方面来自灾后供应商紧急生产的应急物资数量。考虑到政府储备仓库在空间布局上更合理,覆盖受灾点的范围相较于供应商来说更合理,由供应商生产的应急物资都需要经过政府储备仓库中转,然后由政府储备仓库运往受灾点,这在一定程度上可以降低运输成本和提高救灾效率。
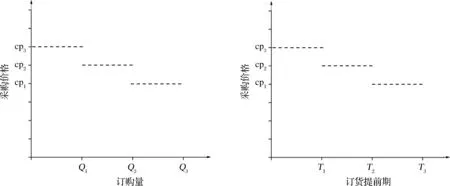
图1 不同订购量和订货提前期下的采购价格策略
目前应急救援阶段划分[21-24]主要根据救援时间或是救援任务的不同进行划分的。本文基于地震灾害救援的特点及地震受灾地需求特点将地震救援分为三个时段,第一时段一般是震后0到24小时内,该时段应急物资需求比较紧迫,此时受灾点需求量主要来自政府储备仓库的实物保障。第二时段是24小时到72小时内,该时段部分路网逐渐恢复,通信开始畅通,该时段的物资需求量大,此时受灾点的需求一部分来自政府储备仓库的实物储备,另一部分来自供应商的生产能力储备。第三时段是72小时到7天内,该时段主要路网基本恢复,通信能够保持畅通,由于政府储备仓库实物储备能力有限,该时段的受灾点需求量主要来自供应商生产能力储备。
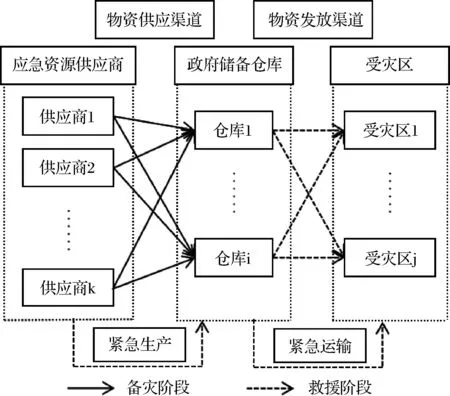
图2 供应商参与机制下应急物资保障策略
2.2 模型构建
2.2.1 模型假设
本文作出如下假设:
(1)政府和供应商签订的合作协议规定了政府灾前从供应商采购的最低的应急物资数量,即最低协议量,以保证供应商所获得的利润。
(2)每一供应商的生产能力不同,灾后不同供应商提供的紧急生产物资受其生产能力的约束。
(3)当地震发生时,供应商和政府储备仓库都会受到不同程度的损害,因此供应商的生产能力和政府储备仓库可使用的库存均受到不同程度的影响。
(4)假定震后各个救援时段的订货提前期为该时段的持续时长。
2.2.2 符号说明
(1)集合
K:应急物资供应商k的集合(k∈K)
I:应急物资政府储备仓库i的集合(i∈I)
J:需求点j的集合(j∈J)
T:应急物资订货提前期t集合(t∈T)
Ξ:震后时段ξ的集合(ξ∈Ξ)
(2)参数
dj(ξ):ξ时段下,需求点j对应急物资的需求量,dj(ξ)是个不确定参数
hij:政府储备仓库i到需求点j的距离
hki:供应商k到政府储备仓库i的距离
cdi:开放政府储备仓库i的固定成本
pck:供应商k的生产能力
sci:政府储备仓库i的储备能力
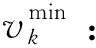
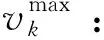
cpk:灾前供应商k提供的应急物资订购量的采购价格
cbkt:灾后供应商k提供的应急物资的采购价格
αi:地震发生后,政府储备仓库i应急物资的可使用库存率
βk:地震发生后,供应商k应急物资的生产能力可使用率
chi:灾前政府储备仓库i储备的应急物资未被使用的单位持有成本
cwkt:任意时段t结束后,供应商k生产的应急物资未被使用的单位持有成本
ct:将应急物资运往受灾点的单位运输成本
cuj:需求点j应急物资需求量未被满足的单位惩罚成本
(3)决策变量

qki:供应商k运往政府储备仓库i的应急物资数量,即灾前的订购量
dqi:政府储备仓库i应急物资库存
mijt(ξ):地震发生后,在ξ时段订货提前期t时,政府储备仓库i运往需求点j的应急物资数量
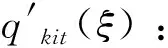
期t时,供应商k生产的需要运往政府储备仓库i的应急物资数量
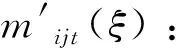
μjt(ξ):地震发生后,在ξ时段结束时,需求点j应急物资未满足需求的数量
rwkt(ξ):地震发生后,在ξ时段结束时,供应商k生产的应急物资的剩余库存
rdi(ξ):地震发生后,在ξ时段结束时,政府储备仓库i应急物资的剩余库存
2.2.3 数学模型构建
对于地震等大规模灾难的发生具有很强的不确定性,其发生后分时段需求情景概率往往是难以估计的,因此,本文建立了通过引入过L1范数定义需求dj(ξ)的不确定性集合,建立更加符合实际的两阶段鲁棒优化模型。这样求解时,只需要利用相关的较少的数据就可以得到比较可靠的结果。鲁棒模型如下:
(1)
s.t.
(2)
(3)
dqi≤yi·sci, ∀i
(4)
(5)
xk∈{0,1}, ∀k
(6)
yi∈{0,1}, ∀i
(7)
其中,
(8)
s.t.
(9)
(10)
rwk,1(ξ)=0, ∀k,ξ
(11)
(12)
(13)
(14)
(15)
本文提出的数学模型是一个两阶段混合整数鲁棒优化模型,目标函数(1)为备灾阶段和地震救援阶段的两个阶段的总成本,(8)为最小化震后最坏情况下的成本。第一阶段成本包括:政府储备仓库的开放成本,从供应商采购的运往政府储备仓库的应急物资采购成本,从供应商运往政府储备仓库的应急物资运输成本。第二阶段成本包括:灾前政府储备仓库储备的应急物资运往受灾点的运输成本,从供应商运往政府储备仓库的应急物资的采购成本和运输成本,供应商生产的应急物资经由政府储备仓库运往受灾点的运输成本,政府储备仓库的剩余应急物资的持有成本,供应商生产的剩余应急物资的持有成本和未满足需求的惩罚成本。约束(2)表示供应商提供的应急物资数量不小于协议中规定的最低协议量;约束(3)表示供应商提供的应急物资数量不超过其最大订购量;约束(4)表示政府储备仓库应急物资的库存不超过其储备能力;约束(5)表示政府储备仓库应急物资库存都是从供应商采购的;约束(6)和约束(7)为0,1变量;约束(9)表示所有供应商生产的应急物资都要经由政府储备仓库运往受灾点;约束(10)表示任意时段下政府储备仓库应急物资的剩余库存关系;约束(11)和约束(12)表示任意时段下供应商开始生产时的供应量为0和运往政府储备仓库的供应量也为0;约束(13)表示任意时段结束时和上一时段结束时的供应商生产的应急物资剩余库存关系;约束(14)表示任意时段下每个需求点应急物资满足程度;约束(15)表示各决策变量为非负数。
3 模型转换

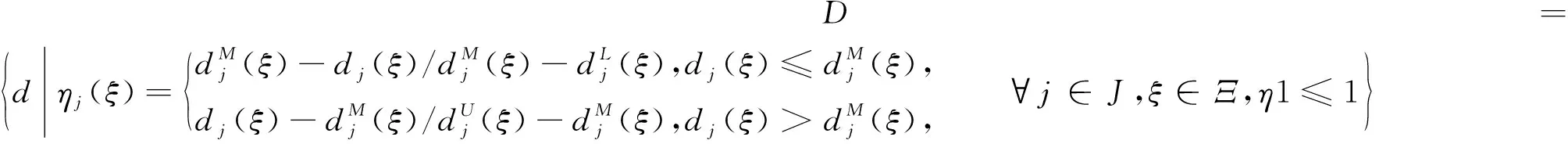
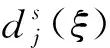
定理1在两阶段鲁棒优化模型2.2.3中,若使用L1范数来定义其中的不确定性集合,则该模型等价于下述模型。
s.t. (2)-(7),(11)-(12)
其中,
(16)
证明:当使用L1范数和对偶理论来定义不确定性集合的方法时,该模型可转化为等价的可求解的确定性方程,即模型(16)。
首先可以求出第二阶段模型的对偶式,即式(8)-(15),为:
s.t.λj(ξ)≤cuj, ∀j,ξ
λj(ξ)+υi≤ct·hij, ∀i,j,ξ
λj(ξ)-γi≤ct·hij, ∀i,j,ξ
θk+γi≤cbkt+ct·hki, ∀i,k,t
υi≤chi, ∀i
(17)
θkt-θk,t-1≤cwkt, ∀k,t
λj(ξ),υi,θk,γifree, ∀i,j,k,ξ
其中,λj(ξ)、υi、θk和γi为引入的对偶变量。同时定义一个闭凸集P,其定义为:
(18)
将式(18)代入模型(17),得:
maxΠ(Q,M,Ξ)
(19)
根据式(19)可将模型(1)改写为如下形式:
(20)
s.t. (2)-(7)
在模型(19)中,若λj(ξ),υi,θk,γi值是确定的,则该模型为一线性规划。最大化问题的最优解肯定在不确定性集合D的某些极点上。由于D为一个带有2n个顶点的凸面体,其中每个顶点均有n-1个元素为最有可能取得的值,而剩下的唯一顶点可能是相应参数的上界或下界。于是模型(20)可用下述模型表示:
s.t. (2)-(7)
(λj(ξ),υi,θk,γi)∈P,∀s=1,2,…,2n}
(21)
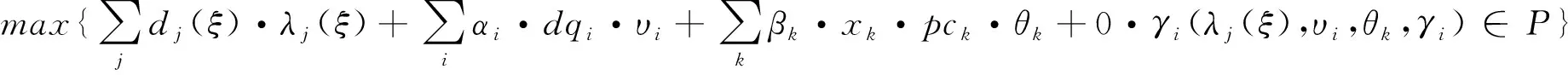
对于∀s=1,2,…,2n。且该模型的对偶为:
(22)
将模型(22)代替模型(21)中的ω的约束条件,得模型(19)相对应的表达式:
s.t. (2)-(7),(11)-(12)
至此,本文中所建立的两阶段鲁棒优化模型转化为等价的模型,利用CPLEX可以进行求解。
4 算例仿真
选取2010年4月14日在青海玉树藏族自治州玉树县发生的7.1级地震作为研究对象,选择特定的11个受灾点,8个备选政府储备仓库,4个备选供应商。本文仅考虑单个应急物资的配置,比如生活用品,在震后3个时段分别满足各受灾点的需求,各时段的时长为订货提前期:24小时内,24-72小时,72小时-7天。玉树地震受灾地区任意时段生活用品的需求量如表1,政府储备仓库储备能力如表2,供应商最低协议量、最大订购量和生产能力如表3。本文采用CPLEX软件对鲁棒对应问题模型求解,将两阶段鲁棒优化模型与随机需求下的模型和均值需求下的模型进行对比分析。
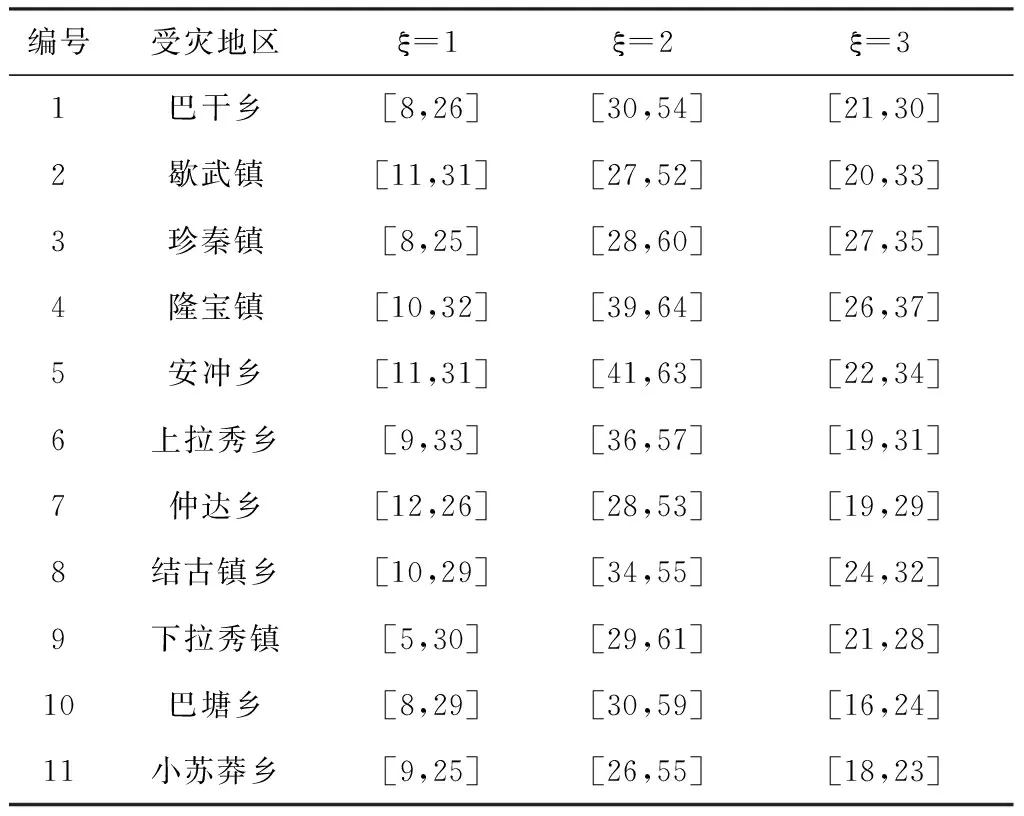
表1 玉树地震受灾地区生活用品的需求量(t)
已知需求点的需求是一不确定参数。当考虑随机需求时,假设需求从各受灾点需求区间随机取10组数据,得到随机需求下的模型目标费用,计算出这十组数据的平均值,与鲁棒模型得出的目标费用比较,同时计算出平均需求下模型的目标费用,实验结

表2 政府储备仓库储备能力
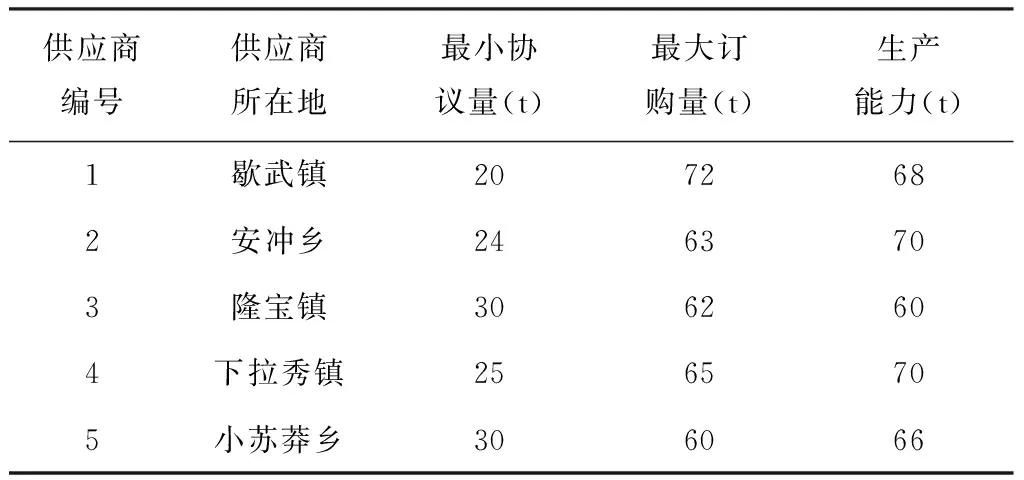
表3 供应商提供的应急物资数量
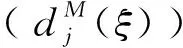
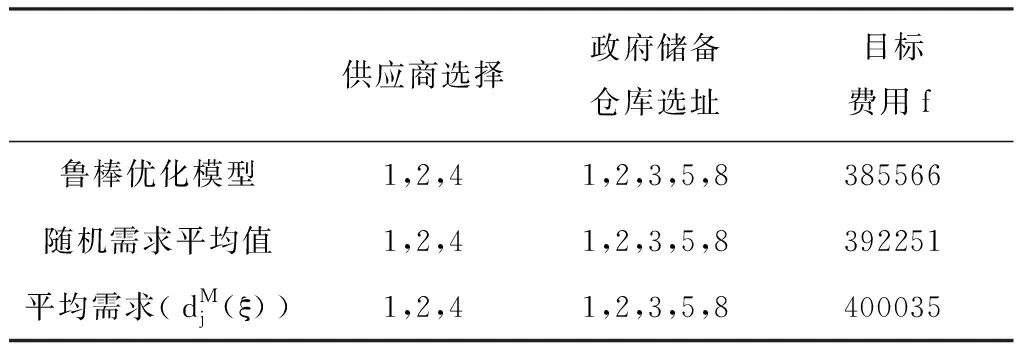
表4 鲁棒模型和随机模型的对比
为了研究模型中不同参数对总成本的影响,本文对灾前供应商最大订购量、最低协议量以及灾后供应商生产能力对总成本的影响进行了敏感度分析,以此为实际情况提供更多的参考价值。灾前最低协议量以初始规定的数量为基准值,从25%基准值到175%基准值变化,将参数带入模型中进行比较分析,结果如图3所示。从图中可以看出,随着灾前最低协议量的不断增大,总成本不断升高。这是由于灾前最低协议量越大,降低了政府从供应商购买应急物资的灵活性和主动性。灾前最大订购量以初始规定的数量为基准值,从25%基准值到175%基准值变化,将参数带入模型中进行比较分析,结果如图4所示。从图中可以看出,随着灾前最大订购量的不断增大,总成本不断降低,因为供应商最大订购量越大,可以获得更多的价格折扣,灾前采购成本降低。此外,灾后采购成本对全过程总成本的影响至关重要,因此本文对灾后供应商生产能力的变化对总成本的影响进行了分析。灾后供应商生产能力以初始规定的数量为基准值,且取值从25%基准值到175%基准值变化,将参数带入模型中进行比较分析,结果如图5所示。结果表明,随着灾后供应商生产能力不断增大,总成本不断降低,因为地震发生后,供应商生产能力越大,满足受灾点需求所需选择的供应商数量更少。由此说明,在实际决策者进行决策时,和灾前最低协议量小或是灾前最大订购量大的供应商合作可以有效地降低总成本。同样地,在与供应商建立合作关系时,灾后生产能力更大的供应商往往可以降低总成本和减少应急资源缺货风险。
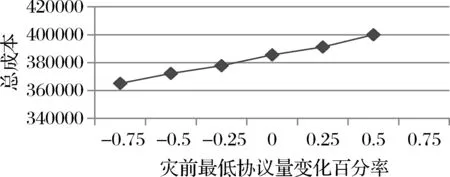
图3 供应商最低协议量变化对总成本的影响
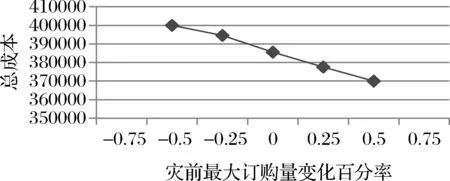
图4 供应商最大订购量变化对总成本的影响
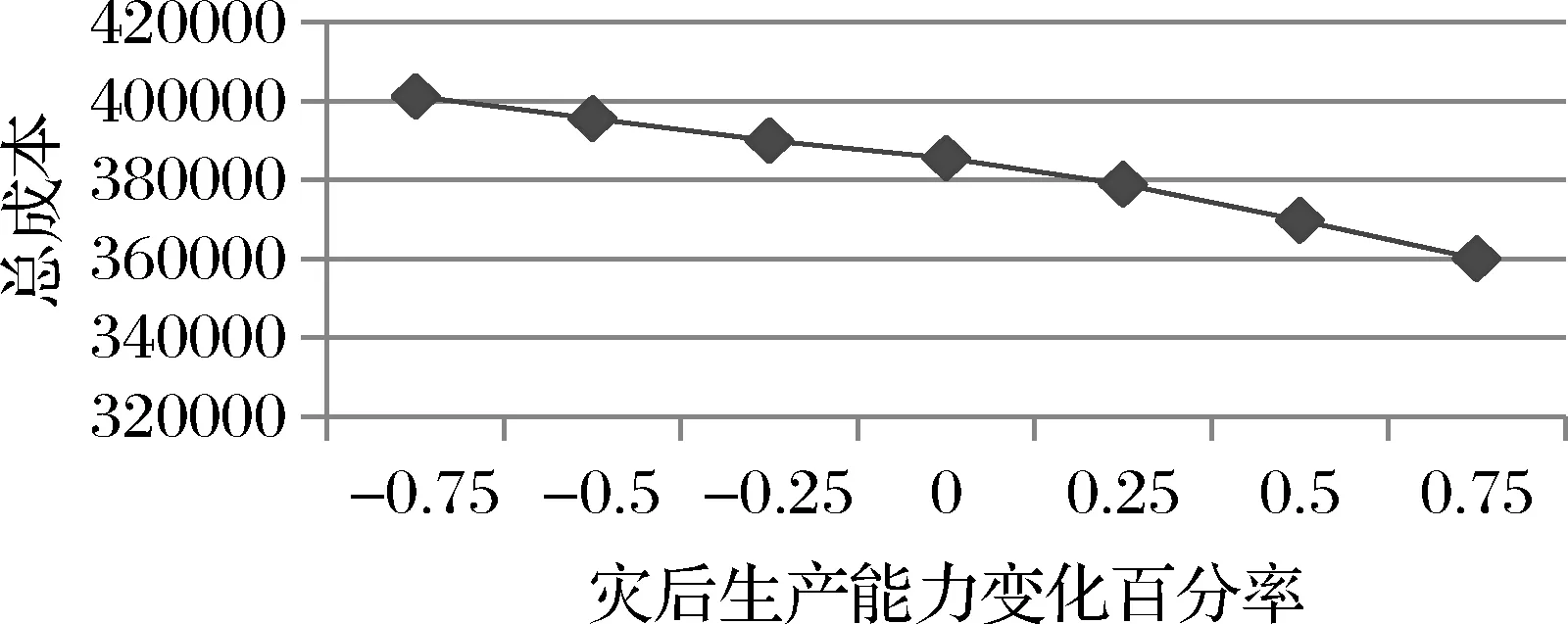
图5 供应商生产能力变化对总成本的影响
5 结语
本文以应对地震灾难为背景研究不确定需求下考虑供应商参与机制的应急资源配置鲁棒优化问题。在满足应急救援响应的分时段应急资源需求的前提下,以最小化应急资源保障体系灾前备灾与地震发生后救灾应急资源保障总成本最低为目标,建立了多个供应商、多个政府储备仓库选址、多个受灾点的两阶段鲁棒优化模型。同时针对应急救援分时段应急资源需求不确定性的特点,本文引入L1范数描述需求的不确定性,给出了鲁棒模型对应问题的转化方法。最后通过算例仿真验证了模型和对应问题转换方法的有效性,为地震的应对提供理论指导和决策支持。
供应商参与机制下的应急资源保障体系建设,在提高应急资源保障效率的同时有效地降低了应急资源保障体系建设的成本。分时段的应急资源需求描述更符合地震救援对应急资源需求的特点。灾前应急物资采购价格与灾后应急物资生产能力采购的价格影响因素不同,协调灾前实物采购与灾后生产能力采购的比例对于降低储备成本具有积极作用。算例分析表明:本文针对不确定需求下考虑供应商参与机制的应急资源配置决策而提出的两阶段鲁棒优化模型及对应问题转换方法的合理性;同时敏感性分析表明了最低协议量、最大订购量和生产能力对总成本的影响,给实际决策者提供了较好的参考作用。
本文仅考虑了灾前订购量与灾后订货提前期对于应急物资供应商采购价格的影响因素,然而有关供应商实物采购与生产能力采购价格还受到其他因素的影响。同时由于突发事件发生带来供应商生产能力降低、地震情景下应急资源需求预测等等都将会使问题更加复杂。供应商参与对应急资源保障体系的建设具有积极作用,后续将深入研究上述相关的问题。

