存在议价能力和副产品协同生产的制造商最优产量决策

周 品, 徐 和, 陆 芬

(1.华中科技大学管理学院，湖北 武汉 430074；2.武汉科技大学管理学院，湖北 武汉 430081)

1 引言

随着环境污染和生态问题日益加剧，公众环境保护的意识逐渐增强，对生活质量提出了更高的要求。同时各国政府相继出台了相关的环境保护措施来进一步规范和管制企业的污染行为。基于公众、政府的双重压力以及企业自身社会责任感的考虑，制造企业需采取有效措施对废弃污染物进行处理以减少对环境的污染。在现实中，常见的废料处理方式有两种：一是企业自身通过传统方式进行处理，比如美铝秦皇岛工厂产生的具有高资源利用价值的危险废物含油硅藻土主要通过水泥窑将其进行焚烧处理[1]；二是将废料外包给处理厂处理，比如蔗糖厂在生产中产生的甘蔗渣主要是卖给下游的造纸厂。可以看到这两种方式存在显著的差异，在第一种处理方式中，企业需要花费一定的处理成本，同时该方式对废料处理之后并未将废料转化为新产品进行销售；在第二种处理方式中，企业可以从废料的交易中获得收益，同时处理厂通过专门的技术对废料进行加工，最终生产出新产品(如：纸)来销售。此外，在实践中，废料的交易价格并非由单个企业(如上游制造企业)来设定的，往往是上游的制造商和下游的处理厂通过协商议价的方式确定最终的废料交易价格，如广西制糖厂将蔗渣打包外卖给制浆造纸企业的出厂价为250元/吨[2]，该交易价格主要是双方协商确定的。鉴于此，本文分析在供应链成员(制造商和处理厂)存在议价能力时，制造商如何确定主产品的产量？成员之间如何通过议价决定废料的交易价格？议价能力会对成员的均衡利润产生怎样的影响？对于制造商而言，采取副产品协同生产是否总是有利的？

本研究主要与副产品协同生产下的最优决策和供应链环境下的纳什议价模型两个领域的研究密切相关。在副产品协同生产的研究方面，目前的研究文献相对较少。其中Lee[3]研究了垄断制造商在可以将废料转化为可销售的副产品时的最优产量和价格决策。Lee和Tongarlak[4]在零售业的背景下分析了需求不确定情形下企业如何决定最优的价格和副产品协同生产策略。程晋石等[5]研究了由制造商和再制造商组成的再制造供应链系统，考虑双方是否实施副产品生产的四种市场结构，得出各种情形下的最优决策。上述研究仅考虑废料是通过自身处理的情形，而在现实中，由于废料处理的技术限制，企业往往通过第三方处理厂来处理。本研究考虑在供应链成员之间存在议价能力的情形下，上游企业如何进行主产品的最优产量决策以及如何通过协商议价方式确定最优的废料交易价格，并进一步分析制造商的最优废料处理策略。从供应链视角出发，李海燕等[6]基于委托代理理论，研究了废弃物提供商与利用商之间的博弈模型，设计了基于用量激励的交易合约机制。陈军和杨影[7]通过构建政府与工业生态链上下游核心企业之间的博弈模型，研究了政府补贴对核心企业产品定价与副产品交易价格的影响。然而李海燕等，陈军和杨影都忽略了副产品协同生产过程中上下游企业的议价能力，而本文在综合考虑副产品协同生产和供应链成员存在议价能力的前提下，分析主产品的产量决策和废料交易价格。

关于供应链环境下的纳什讨价还价模型，学者们进行了大量的研究。其中Bernstein和Marx[8]研究了由单一供应商和多个竞争零售商之间如何通过纳什议价的方式进行供应链总体利润的分配问题。Nagarajan和Bassok[9]研究了单个装配制造商向多个供应商采购互补零部件并装配成最终产品以满足需求的分散供应链系统，同时考虑上游供应商可能组成联盟的情形，研究结果表明，供应链的均衡结构是成员间相对议价能力的函数，同时当制造商的议价能力较低时，上游的供应商会形成稳定的联盟，而当其议价能力较高时，上游的供应商会保持独立，这是制造商更偏好的结果。Guo和Iyer[10]在单个制造商和竞争型零售商的垂直结构下分析了成员间的多边议价问题，研究结果表明当零售商的销售价格差别较小时，制造商更倾向于选择同时议价，而当销售价格差异较大时，制造商更愿意选择顺序议价的方式。Feng和Lu[11-13]采用一般纳什议价(GNB)的框架分析了竞争性供应链的外包决策和契约选择。Hsu等[14]采用基于领导者的合作议价方法(LCB)分析了分散式采购和合作采购下的激励问题。Basak[15]在纳什议价的框架下比较了下游竞争性企业进行产量和价格决策的最优利润，研究结果表明，当最终产品存在替代关系时，产量竞争可以给零售商带来较高的利润，相反，当最终产品存在互补关系时，价格竞争会给最终产品生产者带来较高的利润。赵道致等[16]通过构建基于转换成本的委托代理模型，研究了影响供应链成员议价能力的因素以及这些因素起作用的内在机制。张新鑫等[17]以中国医药市场为背景，研究了企业议价能力和集中采购效率对制药企业集中参与意愿的影响。与上述研究不同的是，本文在副产品协同的背景下来研究上游制造商最优产量决策以及废料的最优交易价格，并将供应链成员在协商议价时的保留利润内生化，最后分析议价能力对成员最优决策的影响。

2 模型描述与假设

考虑由环保型上游制造商和下游处理厂构成的两级供应链结构。上游制造企业在期初投入Q单位的原材料进行产品A(称之为主产品)的生产，产品生产完成之后在主产品市场上销售。假定一单位的原材料可生产出一单位的主产品。同时在主产品生产的过程中会产生γQ单位的废料(在基本模型中假定废料的产出比例为确定的，考虑随机产出比例并不会对本文的结论产生影响，详见3.3节)。鉴于废料对环境的污染以及政府对环保的要求，制造商需对产生的废料进行处理。常见的处理方式有两种：一种是制造商自己采用传统技术进行处理，每单位的处理成本为s；另外一种是制造商将废料卖给具有技术许可的废料处理厂进行处理，每单位废料的销售价格为w。处理厂通过对废料进行加工生产出副产品B并在副产品市场上进行销售。图1描述了制造商与处理厂协同生产的供应链结构。

图1 供应链结构

在现实中，废料的交易价格往往是双方(制造商和处理厂)通过议价(谈判)的方式产生的。双方的议价能力和保留利润决定了最终的废料交易价格。当议价成功时，制造商可从废料交易中获得额外收益，同时处理厂可将废料加工生产成副产品B进行销售从而获取利润。当议价失败之后，制造商将自己进行废料处理，这会对制造商产生处理成本且废料不能转化为副产品B，处理厂也无法获取利润。

不失一般性，我们假定主、副产品的市场需求函数为线性需求(如：Feng和Lu[11],Hsu等[14])，分别为P=a-bQ,P0=a0-b0Q0，在这里a(a0)表示主(副)产品产量为零时的最高价格(即消费者的保留价格)，b(b0)表示消费者对主(副)产品的产量敏感度。当议价成功时，处理厂将废料从上游制造商处全部买回，最终的副产品以市场出清价格进行销售。制造商和处理厂的产品生产成本分别为C和c0。

事件发生的顺序如图2所示。制造商在第一阶段决定主产品的产量Q，同时在生产过程中会产生γQ单位的废料；在第二阶段，制造商和处理厂通过纳什议价的方式决定废料的交易价格w。议价完成之后，处理厂获取废料并对其进行加工生产出副产品，最终在副产品市场上以出清价格进行销售。

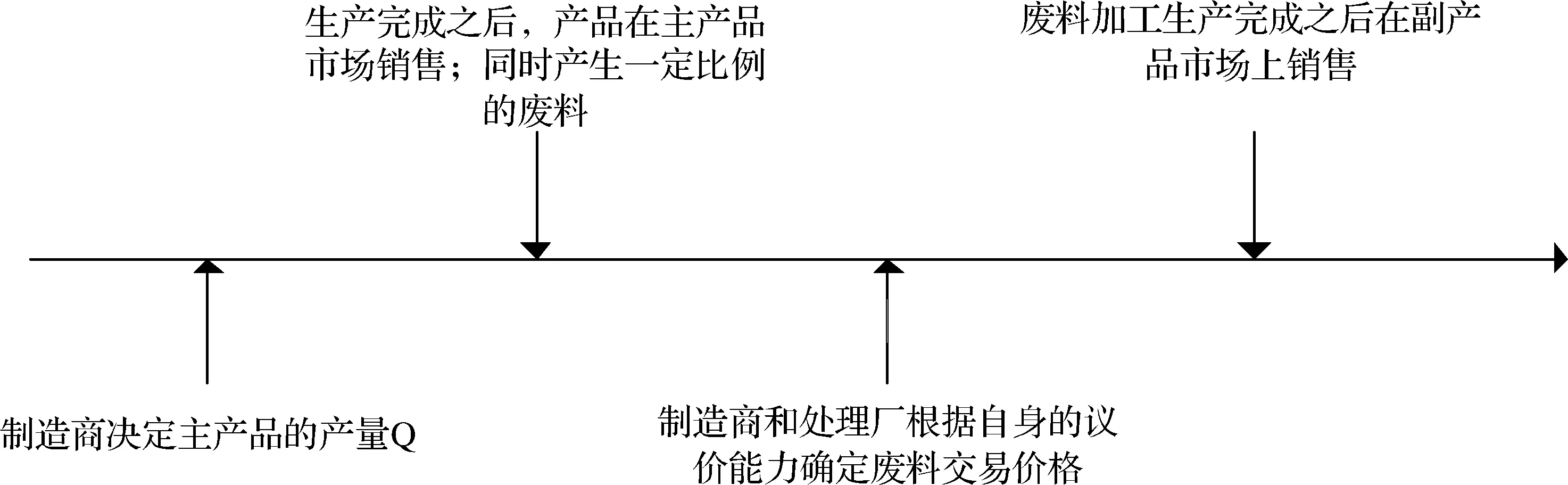
图2 事件发生顺序

3 模型分析

根据事件发生的顺序，该问题可以转化为两阶段的优化决策。通过反向归纳的方法，首先分析第二阶段，在给定制造商在第一阶段的产量Q的前提下，制造商和处理厂在第二阶段最优交易价格的决策，然后分析制造商在第一阶段的最优产量决策。

3.1 最优交易价格的决定

在该阶段，给定制造商在第一阶段主产品产量Q的前提下，制造商和处理厂通过议价决定废料的最优交易价格。为了分析最优交易价格，我们首先给定制造商和处理厂在议价成功时的利润以及议价失败时的保留利润。当议价成功时，废料以w的价格销售给处理厂，处理厂将废料进行加工成副产品，以市场出清价格进行销售。此时制造商和处理厂的利润函数为Πm=(P-C)Q+wγQ,Πp=(P0-w-c0)γQ。

根据文献[8-15]中，一般纳什议价(GNB)的分析框架对纳什产品(Nash Product)的定义,可以得到纳什产品的利润函数为

(1)

命题一：给定制造商在第一阶段的最优生产量Q时，制造商和处理厂之间关于废料的最优交易价格为：

w*(Q)=β(a0-c0-b0γQ)

由命题一可以看到，制造商同处理厂的之间副产品的交易价格取决于双方的保留利润、自身的议价能力以及相关的成本参数。特别的,当β=1时，上游制造商享有绝对的议价权，此时的最优交易价格为w*(Q)=(a0-c0-b0γQ)，同时下游处理厂的利润为零。以下推论给出了相关参数对最优交易价格的影响。

推论一：在给定制造商最优产量决策的前提下，第二阶段的最优交易价格有如下性质：

由推论一的结论可知，废料的交易价格随着制造商保留利润的上升而增加，随着自身议价能力的上升而增加。当制造商自身处理废料的成本上升时，降低制造商的保留利润，从而削弱其议价能力，最终使得交易价格随着废料处理成本的上升而下降。对于处理厂而言，副产品的市场容量上升，使得副产品的市场价格上升，此时的废料交易价格也会随之增加；而当副产品的生产成本上升时，处理厂的单位利润下降，使得废料的交易价格下降。

3.2 最优生产量的决定

在本阶段，制造商需决定主产品的最优产量以最大化两阶段的收益。制造商在第一阶段的利润函数可表示为

Πm(Q)=[P(Q)-C]Q+wγQ

(2)

式(2)中的第一项表示制造商销售主产品的利润，第二项表示制造商销售废料的收益。优化(2)式可得到命题二的结论。

命题二：制造商在第一阶段关于主产品A的最优产量、主产品的均衡销售价格以及制造商和处理厂的最优利润分别为

由命题二的结论可知，制造商在第一阶段的最优产量决策与自身的议价能力和保留利润无关。同时制造商的最优利润函数包含两部分，一部分由自身的议价能力带来的在整个供应链利润中分享的利润；另一部分是由保留利润所带来的收益。而处理厂的利润中除了包含由自身议价能力所分享的利润之外，还有由于制造商的保留利润带来的利润损失。这主要是由于处理厂的保留利润为零。

命题三：存在一点

由命题三可知，制造商并不总是选择将废料给下游处理厂进行加工。当副产品的产量敏感度较大时，处理厂在同制造商议价时所获得的利润会下降，进而废料交易价格下降。这就使得制造商在第一阶段降低主产品的产量，从而获得的利润减少。因此，消费者对副产品产量较敏感时，制造商为了保持自身在主产品销售中获得较高的收益，会选择自己处理废料来获取较高的利润，此时处理厂无法获取废料来生产副产品。相反，当副产品的产量敏感度较小时，制造商更愿意通过与处理厂协商的方式确定均衡的废料交易价格。

在均衡的状态下，制造商的利润随着自身议价能力的上升而增加，而处理厂的利润随着制造商议价能力的上升而下降。这主要是由于当制造商在议价过程中的能力较强(或处于主导地位)时，通过议价会产生较高的废料批发价格，制造商在废料交易中所获得收益会上升，最终会增加总体的利润。同时，当制造商处于强势地位(如β较大)时，处理厂在议价过程中就处于弱势地位，最终形成的均衡交易价格就较高，进而处理厂所获得收益就会下降。

3.3 随机产出的情形

在该部分考虑当制造商产出比例随机时，本文的结论是否依然稳健。假定制造商的废料随机产出比例Υ的均值和方差分别为μ、σ2，其实现值为Υ=γ。事件发生顺序与基本模型类似。需要说明的是，制造商在随机产出比例实现之前决定生产量Qr,而废料产出比例实现之后，制造商与处理厂协商废料批发价格wr。

在第二阶段，给定制造商产量Qr和随机产出比例实现值γ的情况下，纳什产品的利润函数可表示为：

(3)

优化(3)式，可得到：

w*r(Qr)=β(a0-c0-b0γQr)

在第一阶段，制造商决定最优的产量Q以最大化两阶段的利润，此时制造商的利润函数可表示为：

(4)

Pr*

从上式可以发现，在随机产出比例的情况下，制造商的最优产量以及供应量各成员的期望利润函数与基本模型中确定产出的比例的结构类似。同时还可以得到，随着废料产出比例波动性的增加，制造商的产量下降，主产品和副产品的价格上升。而制造商和处理厂的期望利润随着产出波动性的增加而下降。

4 数值实验

本节以确定性废料产出为例，通过算例验证本文的主要结论。首先给出制造商的最优生产策略，其次说明副产品协同生产的价值。相关参数取值如下：顾客愿意支付的主产品、副产品的最高价格分别为a=200、a0=200,主产品、副产品的生产成本为C=20、c0=10,废料处理成本为s=40,废料产出比例为γ=0.9。

4.1 制造商的最优废料处理策略

分别取顾客对主产品、副产品的产量敏感度系数b、b0在区间[0,1]上变化。图3描述了制造商处理废料的最优策略。其中区域“-”表示制造商将废料给下游处理厂加工，区域“+”表示制造商自己处理产生的废料。

图3 制造商废料处理策略

从图3中可以看到，制造商并不总是选择将废料给下游企业处理。具体而言，当顾客对主产品的产量敏感度较高或对副产品的产量敏感度较低的情形下，制造商更愿意将废料给下游企业处理。这主要是由于制造商可从废料销售中获得较高的收益。而当顾客对主产品的产量敏感度较低或对副产品的产量敏感度较高时，制造商更愿意自己来处理。这主要是由于制造商此时从废料销售中所获得的收益较低，同时限制了主产品的生产量。由此可见，制造商和处理厂是一个共生的生产系统，双方的决策相互影响。该结论对于实践中制造企业选择最优的废料处理方式具有借鉴意义。

4.2 副产品协同生产的价值

从图4中可以看到，随着制造商议价能力的增大，制造商通过将废料给下游处理所获得的价值就越高。这主要是由于较高的议价能力可以使制造商向处理厂收取较高的废料交易价格，制造商在副产品协同生产中所获得的收益就较高。因此可见，制造商在废料交易过程中协商能力的大小决定了其在副产品协同生产中所获取的价值大小。

5 结语

本文分析了供应链成员(上游主产品制造商和下游废料处理厂)之间存在议价能力和副产品协同生产时的主产品的最优产量决策以及均衡的废料交易价格。研究结果表明，制造商并不总是选择将废料交由下游处理厂进行加工，这取决于顾客对副产品的产量敏感度。当消费者对副产品产量较敏感时，制造商会选择自己处理废料，此时相对于副产品协同生产而言，制造商可以获得较高的利润；相反，制造商会选择给处理厂进行加工处理。此外，在议价成功时，制造商的均衡利润随着自身议价能力的上升而上升，而处理厂的均衡利润下降。最后本文考虑废料产出随机的情形，发现本文的基本结论依然稳健。本文的结论为实践中制造企业如何选择废料处理方式以及废料交易价格的确定提供了理论依据。需要说明的是，本文仅考虑主产品市场确定的情形，而在现实中企业所面临的是顾客的多样化随机需求，因此分析在不确定需求环境下制造商的最优产量决策是未来的重要研究方向。同时，本文仅研究了废料价格通过议价方式确定，考虑其它的交易机制(如拍卖，竞价)也是一个很有趣的研究问题。

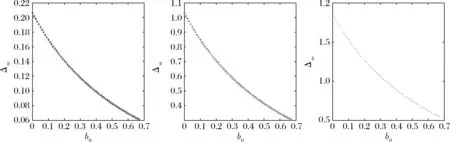
图4 副产品协同生产的价值随β的变化

附录：

命题一的证明：将(1)式关于w分别求一阶导和二阶导可得

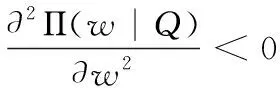
求解上式可得最优的w*(Q)。从而命题一得证。

命题二的证明：将(2)式关于Q分别求一阶导数和二阶导数可得

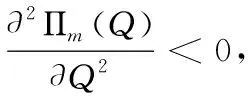
将Q*代入反需求函数P(Q)以及制造商和处理厂的利润函数Πm(Q)、Πp(Q)，可得命题二的结论。从而命题二得证。

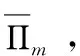
为便于表达，定义：

同时将最优利润函数Πm,Πp分别关于β求导可得：

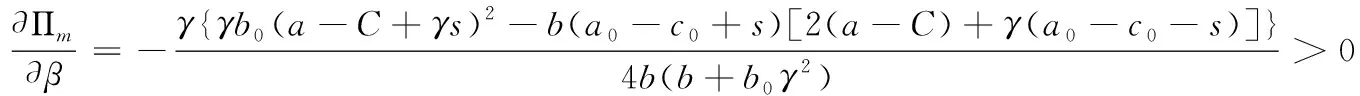
容易得出议价能力对利润函数的影响。从而命题三得证。