基于T–S模糊模型的非线性系统鲁棒采样控制
练红海 ,邓 鹏 ,肖伸平 ,肖会芹
(1.湖南电气职业技术学院风能工程学院,湖南湘潭 411101;2.湖南工业大学电气与信息工程学院,湖南株洲 412008)
1 引言
现代工业过程系统越来越趋于复杂化和大规模化,呈现出混沌、分岔等复杂的非线性行为,若这些行为得不到妥善处理,会导致系统恶化甚至崩溃,使生产遭到巨大损失.因此,非线性系统的控制问题备受关注[1–3].混沌是一种典型的非线性行为,具有无规律和不可预测的行为,这些行为往往会导致系统的性能下降甚至不稳定.近些年,众多学者致力于非线性混沌系统的分析与控制并提出了一些有效的控制方法,例如并行分布补偿控制[4]、时滞反馈控制[5]、滑模控制[6]、脉冲控制[7]等.T–S 模糊模型通过简单的IF–THEN规则结合模糊录属度函数能以任意精度逼近一个连续的非线性函数,该模型具有结构简单,数学描述方便的特点,因而成为描述非线性系统的主要方式[8].由于基于T–S模糊模型描述的非线性系统,可利用线性系统的理论和方法来进行分析与设计,使得各类非线性系统得到了更为深入的研究,例如智能电网系统[9]、高速列车车辆悬挂系统[10]、网络化控制系统[11]等,因此,T–S模糊控制理论被广泛应用到非线性系统控制领域[12–13].
采样控制只需利用采样时刻的系统状态信息,因为它的控制信号在任意一个采样周期内只更新一次(只在数据采样时刻更新),与传统的连续控制相比,这极大的减少了信息的传输量并且提高了控制效率[14],文献[15–16]研究了时变时滞神经网络和混沌神经网络的同步采样控制问题.文献[17]利用模糊采样控制方法讨论了T–S模糊系统的鲁棒耗散问题.对于采样控制系统来说,采样周期是影响系统控制、!效率和性能的重要因素,因为一个大的采样周期可以放松对系统通信容量,带宽的限制要求.因此,设计低保守性的鲁棒镇定条件实现控制器对系统的控制目标且能容忍尽可能大的采样周期具有重要的应用价值和理论意义.基于这个观点,许多学者致力于T–S模糊混沌系统的模糊采样控制[18–24].文献[20–21,24]利用时间相关L–K泛函方法,建立了混沌系统稳定控制器存在的充分条件并设计T–S模糊采样控制器实现了系统的鲁棒镇定.文献[22]使用基于Wirtinger不等式的时间相关不连续Lyapunov泛函方法,提出了模糊采样控制器的设计方案实现了混沌系统的镇定.文献[23]通过两类新的Lyapunov泛函方法即采样间隔分割的Lyapunov泛函方法和基于自由矩阵的不连续Lyapunov泛函方法,讨论T–S模糊混沌系统的采样镇定问题.注意到文献[18–23]仅仅只考虑了采样间隔[tk,t)的系统特征信息,忽视了采样间隔[t,tk+1)的系统特征信息.也就是说,它们并没用充分利用实际采样模型的特征信息.因此,文献[18–23]提出的方法是趋于保守的,还有待进一步研究.
基于此,本文利用Lyapunov理论和模糊采样控制的方法,研究了一类T–S模糊模型的非线性系统的鲁棒采样控制问题.建立了确保系统渐近稳定的低保守性条件并给出了T–S模糊采样状态反馈控制器的设计方法.然后,将提出的方法用于处理混沌Lorenz系统和倒立摆系统的控制问题,仿真结果展示了提出方法的有效性和优越性.其主要贡献归纳如下:1)充分考虑采样间隔[tk,t)和[t,tk+1)的系统特征信息,提出了一个改进的双边时间相关Lyapunov泛函,与文献[18–23]相比,利用了更多的实际采样模型的锯齿结构特征信息;2)基于双边时间相关Lyapunov泛函和自由矩阵不等式,给出了系统鲁棒镇定的充分条件,设计了T–S模糊采样控制器并实现了非线性系统的镇定控制.
整文采用如下记号:0和I分别代表合适维数的零矩阵和单位矩阵;上标“−1”和“T”代表矩阵的逆和转置;R>0表示矩阵R是正定的;sym{N}N+NT代表矩阵N与矩阵N转置之和;diag{·}表示对角阵;“∗”代表矩阵中的对称项.
2 问题描述
考虑一类如下的非线性系统:

式中:x(t)∈Rn是系统状态;u(t)是控制输入;f(·)是一个非线性函数.利用T–S模糊模型,系统(1)可通过IF–THEN规则描述如下:
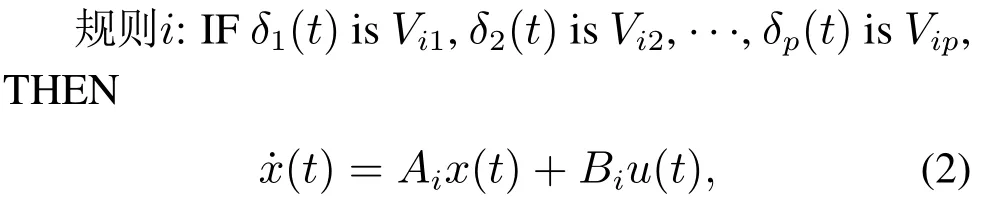
采用单点模糊化,乘积模糊推理和加权平均反模糊化,非线性系统的T–S模糊模型(2)可描述如下:
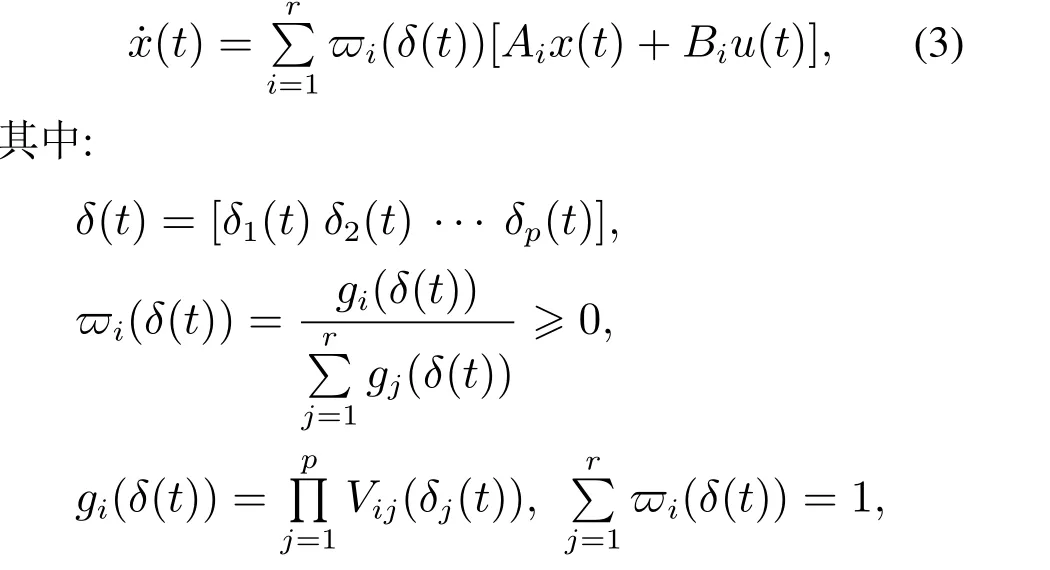
Vij(δj(t))为δj(t)属于模糊集合Vij的隶属度.
根据并行分布补偿算法,设计局部状态反馈控制器,其规则如下:
控制器规则i:IF δ1(t)is Vi1, δ2(t)is Vi2,···,δp(t)is Vip,THEN

其中:Ki为模糊采样局部状态反馈控制器的增益矩阵,控制信号u(t)由零阶保持器(zero-order holder,ZOH)输出产生,tk为ZOH的更新时刻,x(tk)为x(t)在更新时刻tk的离散测量值,那么,T–S模糊采样全局状态反馈控制器可描述为

采样周期为两个相邻连续采样时刻之间的间隔时间,假设满足

其中:hk为某一采样周期,不同k值其大小不同,体现了采样的变周期性,h1和h2分别表示采样周期的最小值和最大值.
将式(5)代入式(3),得到下面的闭环非线性系统的T–S模糊模型:

引入下面的引理,用于系统的稳定性分析和控制器的设计.
引理1(自由矩阵不等式[25])给定正定矩阵R>0,合适维度的自由权矩阵N和任意向量φ0,对所有在[a,b]→Rn上连续可微的函数x,则下面积分不等式成立:

3 主要结论
为了简化公式表达以及推导过程,定义如下标记符:

接下来,基于Lyapunov理论和线性矩阵不等式技术(linear matrix inequality,LMI),给出系统(7)渐近稳定控制器存在的充分条件.
定理1若存在合适维度的对称矩阵P >0,R1>0,R2>0,以及合适维度的矩阵Q1,Q2,X1,X2,Z,N1,N2,F,使得对hk∈[h1,h2],满足LMI:


另外,Ω的定义见引理1,则T–S模糊系统(7)是鲁棒渐近稳定的.
证针对T–S模糊系统(7),构造如下的双边时间相关Lyapunov泛函:

注1构造的Lyapunov泛函V(t)满足

其中i=2,3,···,6.由式(12)知,泛函V(t)在时间上是连续的,即满足条件(12)的泛函也被称之为时间相关Lyapunov泛函,它的特点在于:1)可有效的捕获实际采样模型的特征信息;2)这类Lyapunov泛函只需要在采样时刻正定,无需在整个采样区间内正定,这样可通过放松Lyapunov泛函中的矩阵变量来达到降低系统保守性的目的,如泛函V(t)中的矩阵变量Q1,Q2,X1,X2和Z.因此,这类Lyapunov泛函被广泛用于处理T–S模糊系统的采样控制问题[18–23].另外,受文献[14]的启发,提出的泛函V(t)既与采样间隔[tk,t)的系统特征信息相关,也与[t,tk+1)的系统特征信息相关,所以,将V(t)称之为双边时间相关Lyapunov泛函.
注2注意到文献[18–23]构造的Lyapunov泛函中仅仅只利用了采样间隔[tk,t)的系统特征信息,与之相比,泛函V(t)通过新项Vi(t)(i=2,3,4,5)还利用了采样间隔[t,tk+1)的系统特征信息.也就是说,与文献[18–23]中构造的Lyapunov泛函相比,泛函V(t)利用了更多的系统特征信息,这些信息有助于降低所得条件的保守性,这在实例分析部分得以验证.除此之外,本文构造的Lyapunov泛函还可以用于处理其他复杂系统的综合控制问题,如T–S模糊采样网络控制系统的跟踪控制问题[3],T–S模糊神经网络系统的事件触发控制问题等.
对t ∈[tk,tk+1),计算双边时间相关L–K泛函V(t)对时间t导数得
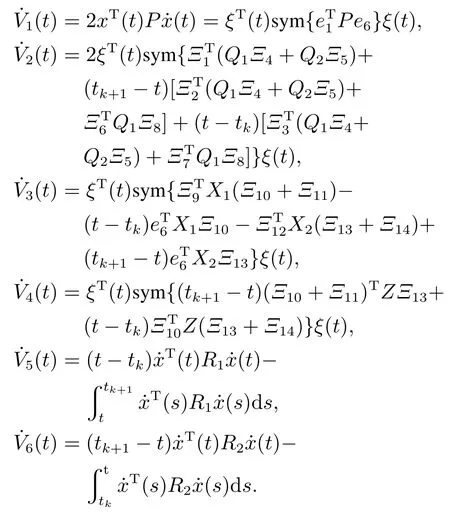
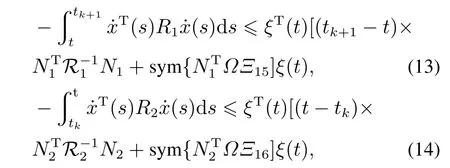
其中: R1diag{R1,3R1}, R2diag{R2,3R2},Ω的定义见引理1.
若存在实数γ1,γ2和γ3以及合适维度的矩阵F,则下式成立:


由Schur补引理知,LMI(9)和LMI(10)等价于Θ1<0和Θ2<0,若Θ1<0 和Θ2<0,则有˙V(t)<0.因此,若LMI(9)和LMI(10)成立,则系统(7)是鲁棒渐近稳定的.证毕.
注3使用Lyapunov泛函分析系统的综合问题,主要通过两方面来降低所得结论的保守性:1)选择的Lyapunov泛函包含尽可能多的有效信息;2)在估计Lyapunov泛函导数时尽可能的缩小其放大程度.关于泛函V(t)的构造在注1和注2进行了详细描述,相对已报道的文献[18–23],V(t)包含了更多的有效信息.另外,在Lyapunov泛函导数的估计方面,相对于文献[18–23]中使用的Jense型不等式即Jense或Wirtinger不等式来说,本文使用的自由矩阵不等式可提供更精确的边界.因此,所得结论比文献[18–23]具有更低保守性.
注4注意到定理1中的LMI是(h1,h2)–相关的,即提出的鲁棒镇定条件既与采样间隔的上界h2相关,也与采样间隔的下界h1相关.文献[18–23]中的条件只与采样间隔的上界h2相关,当设h1=0,定理1也可转换为只与采样间隔的上界h2相关的条件.与文献[18–23]相比,定理1更具一般性.另外,当设h1=h2时,定理1也可用于处理定周期采样的情况.
下面的定理将给出T–S模糊采样状态反馈控制器的设计方法.

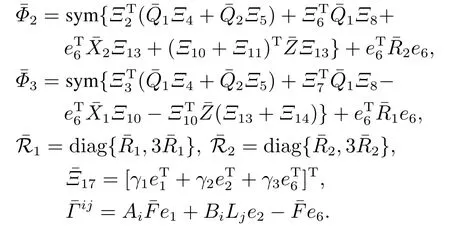
另外,Ξi(i1,2,···,16)的定义见定理1,Ω 的定义见引理1,则系统(7)鲁棒镇定.使系统(7)镇定的模糊采样状态反馈控制器增益为
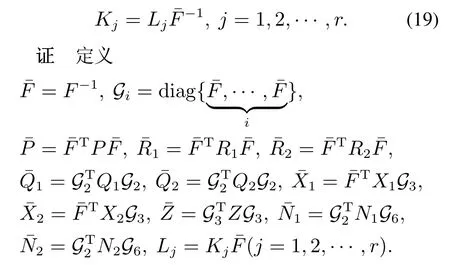
注5定理2涉及到调整参数γ1,γ2和γ3.合适的调整参数对设计一个期望的T–S模糊采样状态反馈控制器十分重要.基于网格搜索算法找出最优调整参数(详见图1),主要步骤如下:1)确定参数γi的取值范围以及它的增量∆γi;2)根据设定的参数,求解定理中的LMI;3)输出最优调整参数以及该参数对应的采样周期和控制率.
4 实例分析
这部分提供4个例子来说明提出方法的有效性和优越性.
例1考虑下面的非线性混沌Lorenz系统[19]:

其中:x1(t)∈[−d,d], a10, b8/3, c28, d25.非线性混沌Lorenz系统(20)可通过具有如下矩阵参数的T–S模糊模型(7)描述:
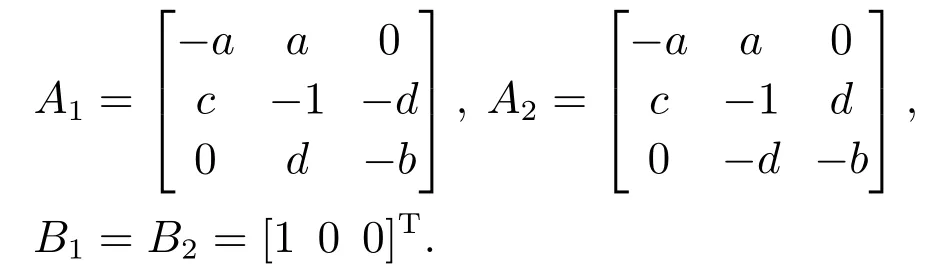
选择模糊隶属度函数为

根据图1给出的算法,设h10,确定调整参数的范围为γi∈[0,5](i1,2,3),增量为∆γi0.01.利用定理2 可得最优调整参数为γ12.60, γ20.01, γ30.04,采样周期的最大允许上界为h20.0444 s,与文献[23]获得的最大允许上界h20.0380 s相比,结果改善了16.8%,即提出的方法可容忍更大的采样周期,说明了提出方法的保守性更低且更有效.

图1 使用定理2找出最优调整参数的流程图Fig.1 Flow chart to find the optimal tuning parameters by Theorem 2
当h20.0444 s时,根据式(19),求得对应T–S模糊采样状态反馈控制器的增益为


图2 当u(t)=0时的系统(20)的混沌轨迹Fig.2 Chaotic trajectories of system(20)with u(t)=0

图3 当u(t)=0时的系统(20)的状态轨迹Fig.3 State trajectories of system(20)with u(t)=0
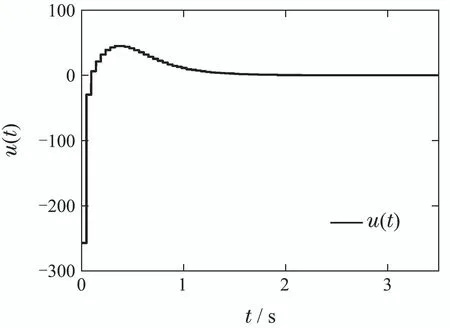
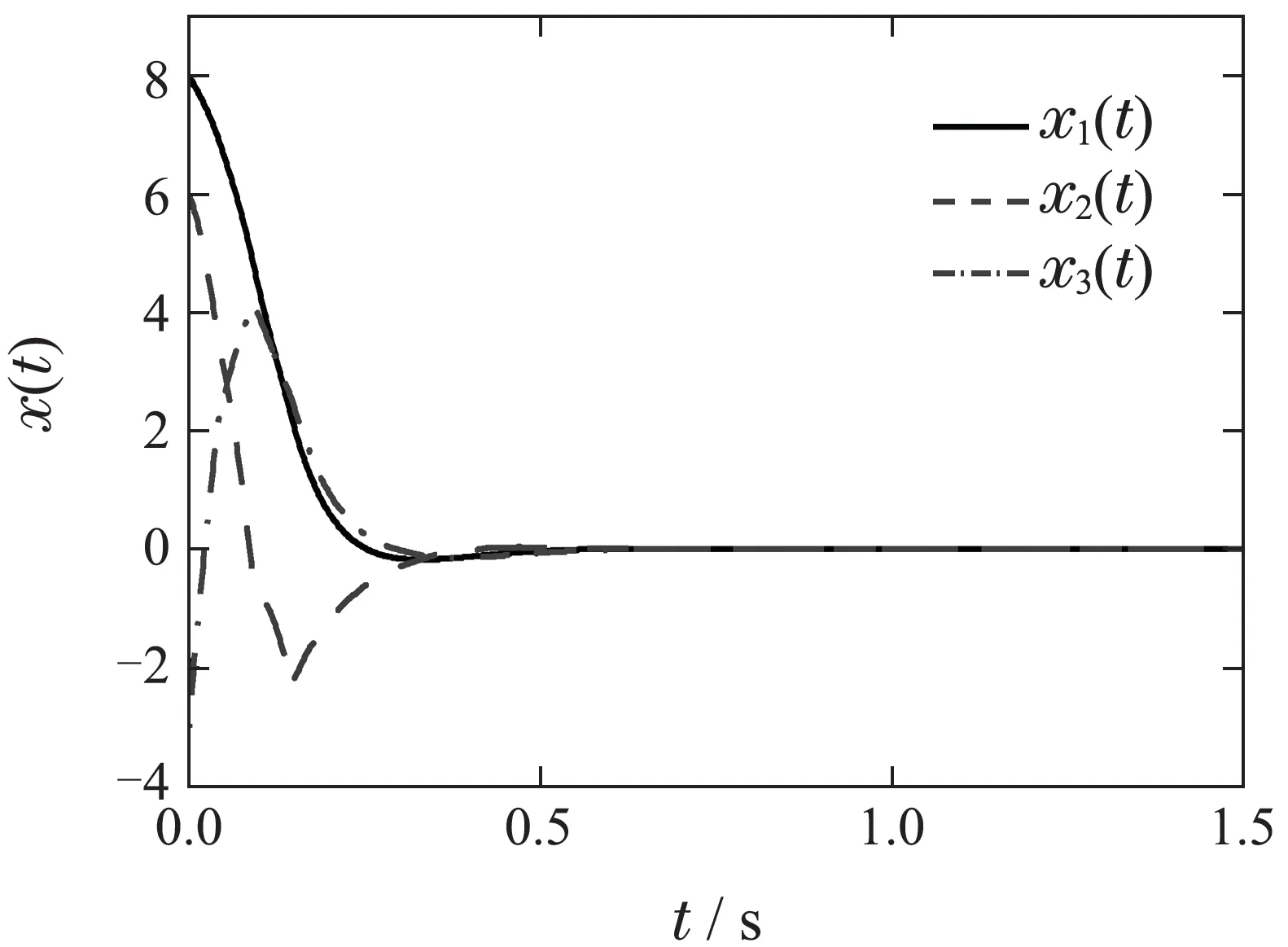
通过使用控制器(21),可得系统的状态轨迹和控制输入如图4–5所示.由图4–5可见,在系统采样周期为hk∈(0,0.0444]的条件下,验证了设计的控制器(21)可有效的控制系统镇定.表明提出方法的可行性.
另外,文献[23]设计的控制器,只有在系统采样周期为hk∈(0,0.0380]的条件下,才能保持系统稳定.当系统采样周期为hk0.0380时,则无法保持系统稳定.而设计的控制器(21)在系统采样周期为0.0380 对于定周期采样情况(即h1h2),选择调整参数为γi(i1,2,3)与变周期采样情况一样,使用定理2(h1h2)计算系统可允许的最大采样周期上界h2列于表1.由表1知,与文献[19–23]中的结果相比,提出方法获得的采样周期上界h2更大,这意味着可以降低信号采样(采样装置)的频率,从而可放松对通信带宽,容量等要求来降低成本.另外,也进一步说明了提出方法比文献[19–23]中的方法具有更低保守性. 图4 变周期采样的系统(20)的状态轨迹Fig.4 State trajectories of system(20)under variable sampling period 图5 变周期采样的系统(20)的控制输入Fig.5 Control input of system(20)under variable sampling 表1 当h1 h2时最大的h2Table 1 Maximum h2 when h1 h2 表1 当h1 h2时最大的h2Table 1 Maximum h2 when h1 h2 当h1h20.0468时,对应的系统T–S模糊采样状态反馈控制器的增益为 基于T–S模糊采样控制器(22),可得系统(20)的状态轨迹和控制器输入如图6–7所示.由图6–7知,在系统采样周期为hk0.0468的条件下,设计的控制器(22)可有效控制Lorenz系统镇定,说明了提出方法的可行性. 图6 定周期采样的系统(20)的状态轨迹Fig.6 State trajectories of system(20)under constant sampling period 图7 定周期采样的系统(20)的控制输入Fig.7 Control input of system(20)under constant sampling 例2考虑如下具有多输入的非线性混沌Lorenz系统[24]: 其中x1(t)∈[−d,d].非线性混沌Lorenz 系统(23)可通过T–S模糊模型(7)进行描述,矩阵参数满足 矩阵A1,A2以及模糊隶属度函数的定义与例1一样. 通过例2进一步说明提出方法的有效性和优越性.首先,根据图1给出的算法,设h10,调整参数的取值范围为γi∈[0,5](i1,2,3),增量为∆γi0.01.通过定理2,可得调整参数γ12.6,γ20.01, γ30.04,采样周期的最大允许上界为h20.0569,对应T–S模糊采样状态反馈控制器的增益如下: 通过不同方法获得的系统采样周期的最大允许上界h2见表2.由表2可见,使用定理2所得的结果与文献[20–21,24]所得的结果相比,有了很大改善,即分别改善了3456.2%,2486.3%,124.9%.表明了定理2相比于文献[20–21,24]中的方法具有很大优越性,同时也说明了定理2的保守性更低. 表2 当h1 0时最大的h2Table 2 Maximum h2 when h1 0 表2 当h1 0时最大的h2Table 2 Maximum h2 when h1 0 图8 系统(23)的状态轨迹Fig.8 State trajectories of system(23) 图9 系统(23)的控制输入Fig.9 Control input of system(23) 例3考虑具有如下矩阵参数的T–S模糊混沌Lorenz系统[23]: 根据图1给出的算法,设h10,,调整参数的取值范围为γi∈[0,5](i1,2,3),增量为∆γi0.01.使用定理2 可得最优调整参数为γ14.45, γ21.05, γ30.25,采样周期的最大允许上界为h20.0643,状态反馈控制器的增益如下: 利用文献[23]中所提方法得到采样周期的最大允许上界为h20.0563,与之相比,本文所得结果改善了14.2%.说明本文方法更加有效. 图10 系统(26)的状态轨迹Fig.10 State trajectories of system(26) 图11 系统(26)的控制输入Fig.11 Control input of system(26) 例4提供一个应用实例–倒立摆系统,进一步说明提出方法的有效性.倒立摆系统的示意图如图8所示[26].利用牛顿定律,得系统的运动方程如下(为了简化表达一些地方“(t)”被省略): 表3 倒立摆系统参数Table 3 The parameters of the pendulum system 图12 倒立摆系统Fig.12 Inverted pendulum system 选择状态变量x1y, x2θ,可得状态空间方程 利用欧拉一阶近似,倒立摆系统可转换为下面的T–S模糊模型: 根据图1给出的算法,设h10,确定调整参数的范围为γi∈[0,5](i1,2,3),以及增量为∆γi0.01.使用定理2可得最优调整参数为γ10.01, γ20.01, γ30.55,采样周期的最大允许上界为h20.3048 s,相应的T–S模糊采样状态反馈控制器的增益为 图13 倒立摆系统的状态轨迹Fig.13 State trajectories of the inverted pendulum system 图14 倒立摆系统的控制输入Fig.14 Control input of the inverted pendulum system 针对T–S模糊混沌系统,利用模糊采样控制方法研究了该系统的鲁棒镇定问题.首先,基于提出的双边时间相关L–K泛函和自由矩阵不等式,建立了系统稳定控制器存在的充分条件,该条件克服了已有方法的保守性且结论更具一般性.然后,基于这个条件,给出了T–S模糊采样状态反馈的设计方法.最后,通过4个实例仿真验证了提出方法的有效性和优越性.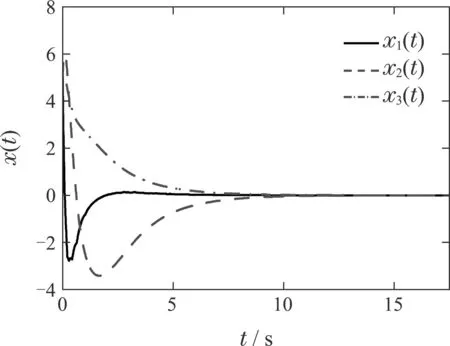






















5 结论

