一类有限Abel群的自同构群

石静静，周 芳

(太原师范学院 数学系，山西 晋中 030619)

0 引言

设G是一个交换群，当G作为循环群的直积时，它的结构是众所周知的，见[1-2]，而AutG的结构还远不为人知.Bidwell和Curran[3]分析了G=Cpm×Cpn(p是奇素数或p=2)的自同构群的结构并给出它的一种简单表示.Bidwell[4]也描述到当G=H1×H2×H3，其中Hi为循环群时，则有

其中

通过利用矩阵表示的方法计算出AutG的结构以及它的生成元和生成关系.

设G=Cpm1×Cpm2×Cpm3(p为素数且m1>m2>m3)，本文采用一种更为简洁的矩阵表示方法从p是奇素数和p=2这两种情况分别给出AutG的结构以及它的一种简单表示.本文的符号是标准的[5].

1 主要内容

1.1 Aut(Cpm1×Cpm2×Cpm3)，p为奇素数

则有

进一步，如果设

正如[7]中，我们可以很自然地去定义：Aij=〈aij〉，它们都是循环的.从而得出AutG=〈a11，a12，a13，a21，a22，a23，a31，a32，a33〉，其中

现详细考虑其余的关系，计算如下：

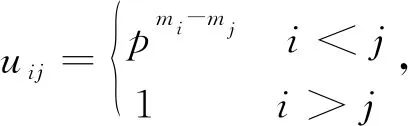
对于aijaji是最复杂的，具体计算如下：

则

最后，我们得到了Aut(Cpm1×Cpm2×Cpm3)的9个生成元之间的生成关系：

Aut(Cpm1×Cpm2×Cpm3)≅〈a11，a12，a13，a21，a22，a23，a31，a32，a33：

1.2 Aut(C2m1×C2m2×C2m3)

则有

AutH1=〈α1〉×〈α11〉≅C2×C2m1-2，

AutH2=〈β1〉×〈α22〉≅C2×C2m2-2，

AutH3=〈γ1〉×〈α33〉≅C2×C2m3-2，

进一步，可设

则子群A11=〈b1，a11〉≅C2×C2m1-2，A22=〈b2，a22〉≅C2×C2m2-2，A33=〈b3，a33〉≅C2×C2m3-2.因此，AutG=〈b1，a11，a12，a13，a21，b2，a22，a23，a31，a32，b3，a33〉.

下面定义阶，具体地，当mi>2，有ο(aii)=2mi-2，若i≠j，有ο(aij)=2min(mi，mj)，且当mi>1，有ο(bi)=2，即：

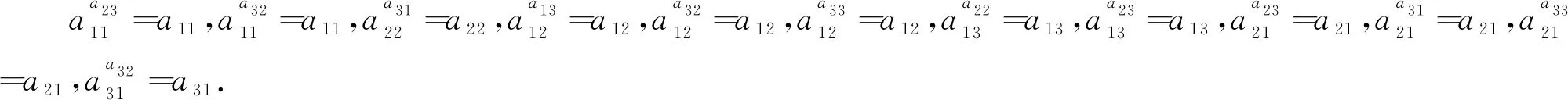
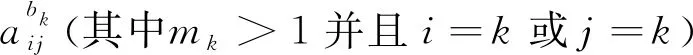
对于ajiaij的形式：

若uij=2：选取ωij(必须为奇数)，使满足-5ωij≡1+uij≡3(mod2mi)，现就a21a12来考虑，具体如下：

最后，得到AutG的12个生成元之间的生成关系：

Aut(G)≅〈b1，a11，a12，a13，a21，b2，a22，a23，a31，a32，b3，a33：