基于斑马带的转子系统轴系扭振测量技术

严丹丹，岳林

(南京航空航天大学 机电学院，江苏 南京 210001)

0 引言

转子轴系是一个结构复杂的弹性连续体，很容易受到周期性变化转矩的影响而产生扭转振动。扭转振动会使轴产生剧烈的应力变化，并会因金属疲劳现象产生裂纹，严重的情况下甚至会由于转子断裂导致相关设备损坏。因此应当特别关注转子轴系的扭转振动现象；同时，当扭转振动频率与轴系的固有频率相近引起共振时，会严重影响工件稳定性，甚至导致工件结构失效断裂。对扭振的准确测量是诊断转子系统故障的基础。

扭振的测量方法分为接触式测量和非接触式测量两种。由于接触式测量方法需要在旋转部件上安装传感器，传感器的信号线需要通过滑环引出，测量系统的成本较高，且需要对原系统的结构进行一定的改进，通用性较差。而非接触测量方法安装简单，通用性更强[1]。

扭振的非接触测量通过测量转子瞬时转速的变化来求得扭振信息。瞬时转速是扭转振动实验中的一个重要测量量，其精度直接影响扭转振动实验的测试精度[2-4]。瞬时转速通过安装在转子上的齿轮、光电编码器发出脉冲的时间间隔以及角度间隔计算得到，而由于在安装、使用这些部件过程中产生的偏差和这些部件原始存在的系统偏差等，这些不可避免的因素必然会对后续扭振分析的精度造成影响。因此在进行扭振分析时，需要对其中一些影响扭振分析的常见因素进行分析和误差校正，从而获得较为准确的瞬时转速值，以保证后续实验的精确性[5-7]。本文主要采用斑马带进行扭振信号采集，其优点是安装简单，仅仅需要粘贴在转子表面，因此适用场合广泛。缺点是由于斑马带上黑白条纹的绘制精度不高，因此各条纹不能看做是等角度分布的，需要在测量之前事先通过算法标定每个条纹所对应的角度。本文对斑马带条纹的角度间隔进行测量和校正，并结合斑马带校正方法对扭振信号瞬时转速计算原理进行改进，提出了一种轴系扭振过程中斑马带脉冲信号的仿真方法；通过仿真信号进行对上述扭振测量方法进行验证。最后，通过扭振测量方法诊断了转子系统的碰磨故障，证明了方法的有效性。

1 扭振测量技术原理

存在扭振的情况下，轴系的转角由刚体旋转和扭振两部分构成，如式(1)。

φ(t)=ω0t+Asin(ωt+ψk)

(1)

式中：ω0t即为轴系的刚体旋转引起的角度变化；ω0为被测轴的旋转角速度；正弦分量为扭振角，A为扭振角振幅，ωt为扭振角频率。

当扭转振动中包含多个频率分量的时候，式(1)可以写作：

(2)

式中ωtk、ψk、Ak分别表示第k个振动分量的旋转角速度、振幅和初始相位。

由式(2)可以得出，在进行扭转角度计算时，需要对测得的轴瞬时角速度进行处理，即去掉轴的平均转速ω0，再对其进行分析，即可得到轴的扭振信号。

1.1 瞬时角速度计算原理

每条斑马带通过激光传感器时的上升沿实际到达时间为t(n)，无扭振情况下，上升沿的理论到达时间为tref(n)，两者之间存在着一定的时间差，如图1所示。对该时间差进行处理，即可得到轴系的扭振角速度和扭振角度(本刊黑白印刷，相关疑问咨询作者)。

图1 带扭振和无扭振信号的对比

假设转子系统上斑马带的数量为B，则转轴旋转第j圈的时间T为：

T(j)=t(B(j+1))-t(B·j)

(3)

其中经过第j圈中第b个条纹所对应的时间Δtj(b)为：

Δtj(b)=t(B·j+b+1)-t(B·j+b),1≤b≤B

(4)

经过第b个条纹时轴的瞬时转速如式(5)所示。

(5)

其中r(b)代表每条斑马带在一圈中的占比，若斑马带条纹等分，则每条斑马带的占比为：

(6)

之后，对瞬时转速进行数值积分即可得到转子的扭振角度。

1.2 斑马带测量扭振的误差及校正

在实际情况中，斑马条纹分布是不均匀的，斑马带的误差会对后续扭振计算过程中带来误差，因此需要对斑马带条纹宽度进行校正。

已知第j圈中第b个条纹的通过时间Δtj(b)以及轴系第j圈的通过时间T(j)，轴在匀速旋转的前提下，两者的比值近似于第b个条纹在一圈中的占比，如式(7)所示。

(7)

但由于扭振以及测量误差的存在，rj(b)和真实的占比还存在着一定的差距，该差值在0上下浮动，因此通过平均可以使误差相互抵消，使测量结果更加接近真实的占比，如式(8)所示。

(8)

2 仿真信号分析

2.1 斑马带脉冲信号仿真

带有扭振的情况下，转子在tn时刻的扭转角度如式(9)所示。

(9)

式中：V0为起始转频；α为转子的角加速度；tn为信号中的第n个采样时刻；θ(tn)为由转子扭振引起的转角。

从最后一个上升沿的开始时刻到tn时刻，转子转过的角度γ(tn)为：

(10)

式中：R为每个条纹所占的角度，符号“⎣」”为取整符号，⎣x」表示一个小于或等于x的最大整数。

根据γ(tn)与R的比值，判断传感器在当前条纹中的位置：转速脉冲的上升沿、高电平或者低电平。

(11)

脉冲仿真信号在上升沿、高电平段和低电平段分别满足如下的函数：

(12)

2.2 不均匀斑马带校正

为验证斑马带校正方法的准确性，根据2.1的信号仿真原理，生成一组斑马带不均匀的匀速脉冲信号，其仿真参数如表1所示。

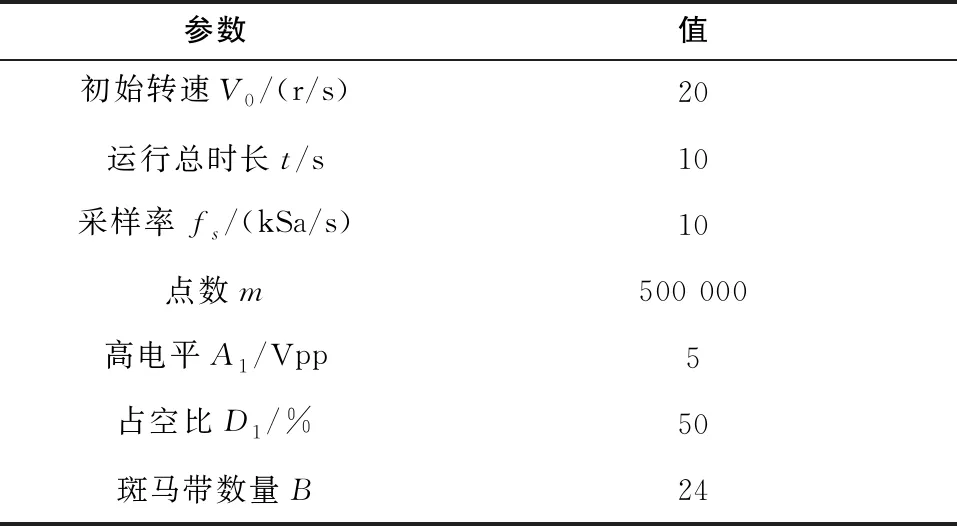
表1 匀速信号参数

仿真信号中的条纹数B=24，条纹的实际宽度占比在1/24上下随机浮动，如图2中的星号所示。根据1.2节中的方法求得的条纹占比如图2中的圆圈所示。可以看出，计算所得的占比与仿真值相吻合，其相对误差接近于0，说明本文采用的误差校正方法是可行的。

图2 不均匀斑马带仿真校正

将不均匀斑马带占比植入仿真脉冲信号，采用前文中瞬时转速和扭转角度的计算方法，可得到考虑和不考虑斑马带补偿情况下的瞬时转速和扭转角度，如图3、图4所示。可以看出，在不考虑斑马带不均匀性的情况下得到的瞬时转速和扭转角度有巨大的误差，而采用了本文的条纹宽度校正方法后，求得的瞬时速度和扭转角度和原始仿真值吻合得很好。

图3 瞬时速度

图4 扭转角度

3 实验验证

验证本文方法的双盘转子系统实验台如图5所示。CUT-2转子实验台主要包括转速调节器、电机、双盘转子系统、联轴器、两支激光转速传感器、两个轴承座、底座以及斑马带等。斑马带上的黑白条纹宽度大致相等，且交替分布。斑马带附着在转子圆柱面上，跟随转子同步扭振。1号激光转速传感器被放置在联轴器附近，该传感器一圈仅发出一个脉冲，作为参照信号，用于确定斑马带上各条纹的编号。2号激光转速传感器对准斑马带，用于计算扭振角速度和扭振角度。

图5 扭振测量实验系统

本次实验采用的斑马带白色条纹数目为24，条纹宽度为10 mm。采用前文的方法对斑马带占比进行标定。标定时，利用转速调节器将双盘转子系统的转速控制在200 r/min低速匀速转动，系统采样率设置为102.4 k。标定结果的最大相对误差<4%。

转子在3 100r/min运行时的瞬时转速如图6所示。可以看出，由于180圈～320圈附近发生碰磨，瞬时转速有明显的变化，如图7所示。通过对健康状态下和碰磨状态下260圈附近的瞬时转速计算所得的扭转角度进行阶次分析，得到的阶次谱图如图8和图9所示。从图中可以看出，在健康状态下生成的1阶谱幅值为0.248，而在碰磨情况下1阶幅值为0.287，后5阶幅值在碰磨状态下相较于健康状态的幅值都有所增大。由于两次实验的差别仅仅在于第2次实验对CUT-2实验台用黄铜碰磨螺钉进行了碰磨，因此可认为扭转角度阶次谱幅值增大是碰磨的原因造成。

图6 健康状态下的瞬时转速

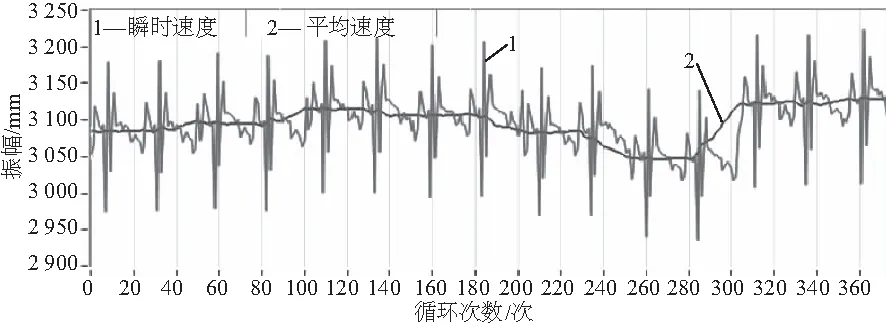
图7 碰磨情况下的瞬时转速

图8 健康状态下扭振角度的阶次谱

图9 碰磨状态下扭振角度的阶次谱

4 结语

本文论述了基于斑马带进行扭振测量的技术难点，并采取了合理的解决方法。对利用斑马带进行信号采集过程中产生的误差进行测量和校正。提出了一种扭振脉冲仿真信号的生成方法，结合斑马带校正方法对扭振信号瞬时转速计算原理进行改进，并根据计算所得的瞬时角速度和扭转角度进行分析。最后，通过一组转子系统碰磨实验验证了方法的有效性。

主要结论如下：

1) 在采用斑马带补偿改进的算法计算所得瞬时转速和扭转角度的精度得到极大的提高。

2) 采用斑马带补偿改进的算法所得的扭振固有频率的精度更高。

3) 碰磨发生后，转子的扭振振幅出现了明显的变化，可以据此识别出扭振故障。