复材双搭胶接结构应力分析与试验研究

邵金涛，周晚林，李鹏，仇晓今，朱苏纬

(1. 南京航空航天大学 机电学院，江苏 南京 210016； 2. 南京财经大学 公共管理学院，江苏 南京 210023)

0 引言

复材双搭胶接结构已经越来越多地用于航空工业[1]。统计数据表明，大约70%的双搭胶接结构失效发生在接头处，且接头的主导破坏是胶层剪切破坏[2]。目前，理论分析方法是对层压板常采用线弹性假设，对胶层采用线弹性或理想弹塑性假设[1]。DELALE F等[3]针对胶层应力分析得到了一个修正的本构方程。郭凯特等[4]考虑了搭接区阶梯末端截面积变化细节。试验测定法现阶段主要应用于复材螺栓连接中[5]。对于双搭胶接结构虽然载荷路径偏心确实存在，但由于其侧向对称没有总体的弯曲变形且在胶层很薄的情况下，外搭接板的弯曲变形很小，可忽略不计[1]。为进一步提高试验测量精度，本文根据测量的应变分别提出了基于经典弹性理论和基于经典层压板理论的应力计算方法。

1 应力分析理论模型

1.1 问题描述

研究如图1所示双搭胶接结构的应力分布，P为内搭接板单位宽度内所受的轴向拉力。由于接头结构和载荷具有对称性，可取结构的一半进行分析。

图1 复材双搭胶接接头模型

1.2 基本假设

1) 忽略胶层中的剥离应力，且胶层中的剪应力沿厚度方向为常值；

2) 搭接板中的纵向应力沿厚度方向为常值；

3) 搭接板和胶层都是线弹性的。

1.3 应力分析理论模型的建立

以双搭胶接接头微元体为研究对象进行受力分析，如图2所示。可得平衡方程式(1)、式(2)。

图2 双搭胶接接头微元体受力分析

(1)

(2)

式中：To、Ti分别表示胶接接头处外搭接板和内搭接板单位宽度内所受的轴向拉力；τ为胶层剪应力。

胶接接头中内外搭接板位移-应变的关系如下：

(3)

(4)

式中：uo、εo、Eo和to分别为外搭接板的纵向位移、纵向应变、等效拉伸弹性模量和厚度；ui、εi、Ei和ti分别是内搭接板的纵向位移、纵向应变、等效拉伸弹性模量和厚度。

胶层剪应力与内外搭接板的纵向位移关系为：

(5)

式中：Ga为胶层切变模量；η为胶层厚度。

对式(1)、式(5)两边求导，并综合式(3)、式(4)可得：

(6)

根据图2中双搭胶接接头的受力分析，可得：

P=Ti+2To

(7)

将式(7)代入式(6)，可得：

(8)

其中：

(9)

计算得出接头处胶层剪应力的分布函数：

(10)

2 试验件的应变测量与应力计算

2.1 试验件制作

试验采用碳纤维增强环氧树脂基复合材料层压板，牌号为T700/FRD-YG-40S，单层名义厚度0.13 mm，力学性能如表1所示，铺层顺序为[45/-45/0/45/90/-45/0/45/0/-45/90/45/0]s。根据ASTM D 3528[6]标准进行试验件设计，其基本尺寸如图3所示。试验使用的胶粘剂为环氧结构胶，牌号为JEAOBOND EP-5230，其力学性能如表2所示，胶粘剂固化采用加温固化，固化温度为85 ℃，固化时间为60 min。加热固化后，需回温24 h方可测其力学性能[7]。

图3 双搭接连接接头图(单位：mm)

表1 T700/FRD-YG-40S材料属性

表2 JEAOBOND EP-5230的力学性能

2.2 试验过程

设计如下应变计粘贴布局：试验件应变计的粘贴位置如图4所示。

图4 外搭接板应变计粘贴位置图

应变分布测量试验在天辰WES-100B万能力学拉伸试验机上完成，应变由KD7016静态应变测量仪测量。拉伸机施加不致胶层损伤的中小载荷，应变分布测量的试验参数配置如表3所示。所有试验的实验室温度控制在(22±4)℃[8]。

表3 复材双搭胶接结构应变分布测试参数配置

表3中配置2外搭接板上表面各位置应变平均值见表4。

表4 应变测量平均值

2.3 应力计算

1)基于经典弹性理论的应力计算方法

由复合材料力学相关知识可知：层压板的应变可以等效为拉伸导致的中面应变和弯曲应变两部分组成，沿着厚度方向线性分布,关系表达式为：

(11)

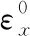
本文将由载荷路径偏心导致的不均匀内力等效为一个均匀内力和一个弯矩组合。该方法也类似地被LANGELLA A[9]等人在单搭胶接结构应力分析中使用，对复材层压板单搭偏心载荷的分析有着非常好的效果，等效受力情况如图5所示。

图5 层压板受力等效图

图5中:Nx表示水平内力；M表示等效弯矩。

基于此，表层由于弯矩导致的应变绝对值可以由以下公式求出：

(12)

通过消除弯矩导致的应变，可修正得到由拉伸载荷导致的应变：

(13)

因此：

(14)

(15)

(16)

τE(x)即为基于经典弹性理论应力计算方法计算得到的接头处胶层剪应力分布函数。

2) 基于经典层压板理论的应力计算方法

复材双搭胶接结构单向拉伸时，单层板的剪应变γxy很小，暂且忽略不计[1]。因此，层压板中第k层的纵向应力：

(17)

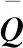
(18)

(19)

τC(x)即为基于经典层压板理论应力计算方法计算得到的接头处胶层剪应力分布函数。

3 应力计算结果分析与比较

通过数据处理得到如图6所示的应力曲线图。

3种方法分析得到的复材双搭胶接结构接头处胶层剪应力分布曲线如图6所示。胶层剪应力分布曲线有良好的重合度，峰值都出现在接头端部,说明接头端部是最危险的位置，峰值相差不超过10.9%，验证了理论模型的有效性。从图6可知，在长度相同的情况下，胶层剪应力随着载荷水平的升高而增大。而在相同的拉伸载荷作用下，当搭接长度达到一定的数值时，无论怎样增加搭接长度，胶层剪应力的峰值基本不再增加。

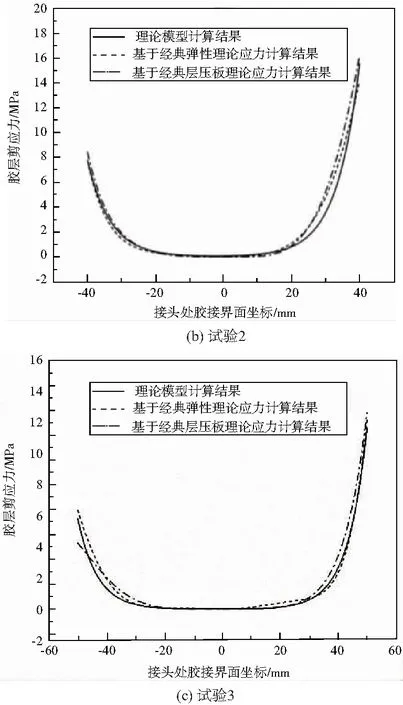
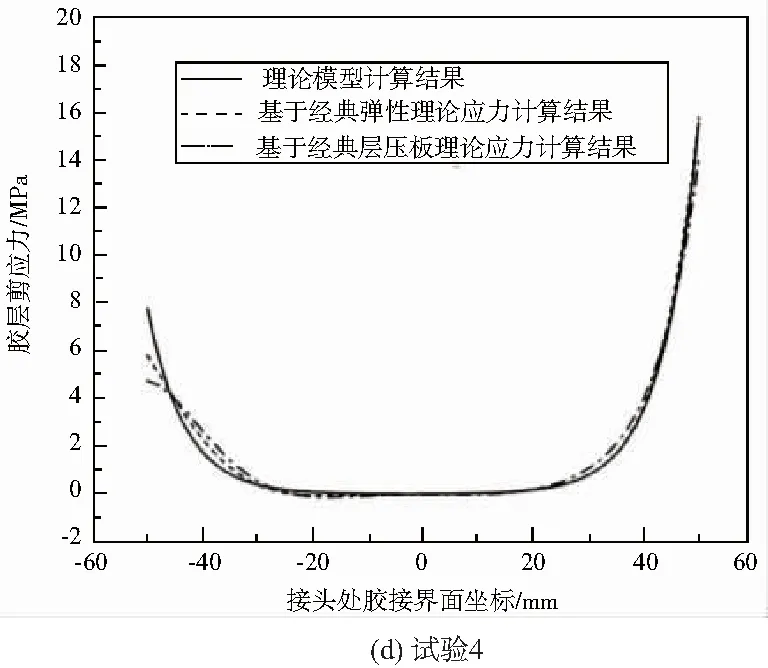
图6 不同分析方法得到的接头处胶层剪应力分布

4 结语

1) 通过与应力计算方法得到的结果进行对比，验证了本文基于经典弹性理论建立的复材双搭胶接结构应力分析理论模型的有效性。

2) 在修正复材双搭胶接结构在拉伸载荷作用下载荷路径偏心导致弯曲和忽略单层板剪切变形的基础上，提出了基于经典弹性理论和基于经典层压板理论的应力计算方法。

3) 试验与理论分析结果表明：胶层剪应力峰值出现在接头端部。在长度相同的情况下，胶层剪应力随着载荷水平的升高而增大。在相同拉伸载荷作用下，当搭接长度达到一定的数值后，胶层剪应力的峰值基本不再增加。