卡箍动力学特性研究

吕金华，臧朝平，许本胜, 2，刘忠华，张让威

(1. 南京航空航天大学 能源与动力学院，江苏 南京 210016； 2. 桂林航天工业学院 机械工程学院，广西 桂林 541004)3. 中国航空工业集团 沈阳发动机设计研究所，辽宁 沈阳 110000)

0 引言

航空发动机外部管路主要用于输送燃油、滑油和空气等介质，是发动机附件系统的重要组成部分。在航空发动机的使用过程中外部管路常发生断裂、漏油等故障，振动是管路断裂的主要原因和诱导因素[1]。卡箍是在航空发动机外部管路中起增强管路刚度、紧固管路位置的重要零件，卡箍对管路系统振动特性具有重要影响[2]。

冯凯等人利用有限元法分析了不同数量、位置的卡箍对管路固有频率的影响，并以此为依据进行了管路调频[3]。刘伟等人将卡箍视为末端固定的平移约束弹簧单元，讨论了卡箍数量和刚度对管路系统动力学特性的影响[4]。KWONG A H M等人采用遗传算法对管路卡箍布局进行了优化，并用试验验证了其理论的可靠性[5]。目前的研究多集中于卡箍布局对管路特性的影响，而忽视了对卡箍自身动力学特性的研究。

本文首先对卡箍直管系统在不同拧紧力矩下进行模型试验，研究拧紧力矩对卡箍刚度的影响；其次对卡箍处于不同位置的直管系统进行试验和仿真研究，验证本文得到的卡箍刚度与拧紧力矩的函数关系，对管路系统设计具有重要的指导意义。

1 基于测试数据辨识卡箍刚度及相关性分析

基于模态试验数据辨识卡箍刚度的流程如图1所示。对卡箍直管系统进行模态试验，利用试验数据对卡箍直管系统有限元模型中的刚度参数进行修正，使有限元模型的分析结果与试验结果的误差满足要求，获得可以反映实际卡箍动力学特性的刚度参数。对卡箍直管系统在不同拧紧力矩下进行模态试验，利用试验数据辨识卡箍在不同拧紧力矩下的刚度参数，得到卡箍刚度与拧紧力矩的函数关系。

图1 基于测试数据辨识卡箍刚度流程

相关性分析的主要目的是分析有限元模型和实际结构之间的误差程度，以判断是否需要对有限元模型进行修正。如果有限元模型与实际结构之间的相关性较差，说明有限元模型无法准确反映实际结构的动力学特性，需要对模型进行修正。常用的相关性分析评判标准有频差，模态置信准则为MAC。

频差为有限元模型的仿真固有频率与实际结构对应的试验频率之间的差异，表达式为：

(1)

其中：fi为有限元模型的第i阶仿真频率;fit为实际结构的第i阶固有频率。

工程上，模态置信准则(MAC)被广泛应用为模态振型的相关程度。MAC值公式为：

(2)

MAC值的取值范围为0～1，一般认为，MAC值超过0.6可以认为两阶振型是相关的，MAC值低于0.2，则可认为两阶振型是不相关的。

2 拧紧力矩对卡箍刚度影响

2.1 卡箍直管系统在不同拧紧力矩下的模态试验

本文研究的卡箍直管系统如图2所示。直管为不锈钢管，长400 mm，外径为9.5 mm，内径为7.5 mm。直管左端伸进夹具40 mm，卡箍距离直管右端40 mm，卡箍拧紧力矩为1 Nm。整个实验在铸铁平台上完成，最大程度地降低了环境的影响。

图2 卡箍直管系统

卡箍直管系统模态试验如图3所示。由于卡箍结构的不对称性，分别在水平、竖直两个方向对卡箍直管系统进行模态试验。在直管表面从固支处每隔40 mm布置1个测点，共布置10个测点。在1号测点左边附近激励，用多普勒激光测振仪逐个采集各个测点的速度响应数据[6-7]。通过水平、竖直两个方向的模态试验，可以得到卡箍直管系统在1 Nm拧紧力矩下的前3阶模态频率和模态振型，分别如图4和表1所示。卡箍直管系统1、3阶振型为水平弯曲，2阶振型为竖直弯曲。

图3 卡箍直管系统模态试验

图4 卡箍直管系统前3阶模态振型

在2～7 Nm范围内，以1 Nm为步长，共取6个拧紧力矩值，分别作为图3中卡箍的拧紧力矩，重复上述试验，得到卡箍直管系统分别在1～7 Nm拧紧力矩下的前3阶模态频率，如表1所示。

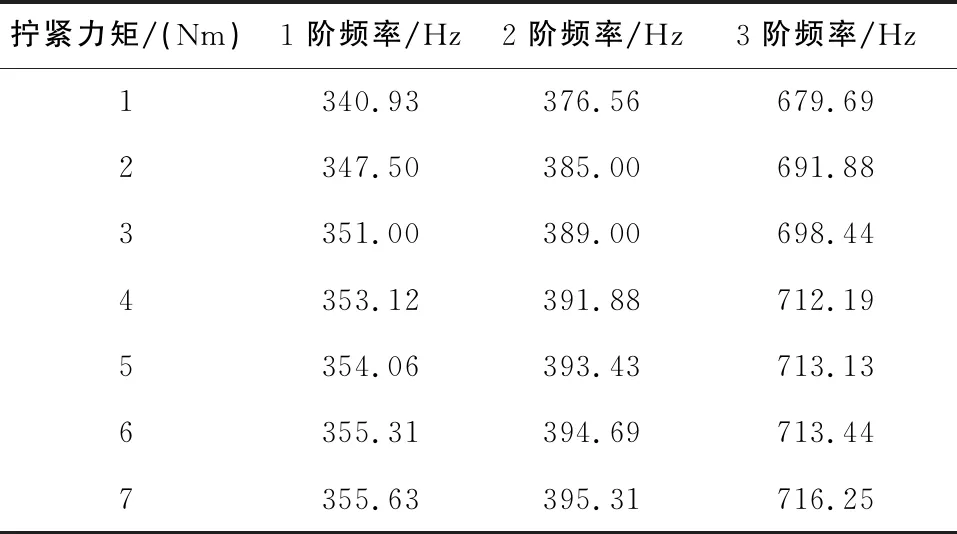
表1 卡箍直管系统在1～7 Nm拧紧力矩下的前3阶频率

各阶频率随着拧紧力矩的增大而增大，且都在6 Nm处趋于稳定。比较卡箍直管系统分别在1 Nm和7 Nm拧紧力矩下的各阶频率，1阶提高了4.31%，2阶提高了4.98%，3阶提高了5.38%。这说明拧紧力矩对卡箍的刚度具有明显的影响。

2.2 卡箍直管系统的建模

卡箍直管系统有限元模型示意图如图5所示。直管由40个梁单元组成，单元截面为同心圆，内径为7.5 mm，外径为9.5 mm。梁单元材料参数如表2所示。考虑到直管的加工误差，根据直管的实际质量，对直管的密度进行了修正。

图5 卡箍直管系统示意图

表2 梁单元材料参数

由2.1节试验可知，卡箍直管系统1、2阶振型相似，方向不同，但是频率相差较大，这说明卡箍的水平刚度与竖直刚度相差较大。因此，本文建立水平弹簧单元和竖直弹簧单元以分别考虑卡箍的水平刚度、竖直刚度。卡箍对管路的实际约束接近于固支约束，但是仅在卡箍中间位置建立一个水平弹簧单元和竖直弹簧单元无法限制管路的转动自由度。因此本文在卡箍的左右两侧各建立一个水平弹簧单元和竖直弹簧单元来模拟卡箍对管路的实际约束。同时在卡箍的中间位置建立一个质量单元以考虑卡箍的质量。为了简化分析，认为卡箍左右两侧同方向上的弹簧单元参数一致，如表3所示。

表3 卡箍简化模型中的单元参数

在直管左端施加固支约束，对卡箍直管系统有限元模型进行模态分析，得到前3阶模态频率如表4所示。与卡箍直管系统在各个拧紧力矩下的试验结果对比如表5所示。1阶模态的最小频差为-6.49%，2阶模态的最小频差为4.22%，3阶模态的最小频差为-31.59%。这说明有限元模型中的卡箍刚度参数无法反映实际卡箍在各个拧紧力矩下的刚度特性，需要对其进行修正。

表4 卡箍直管系统模态分析结果

表5 卡箍直管系统模态分析结果与试验结果对比

2.3 模型修正

以卡箍直管系统的试验频率作为修正目标，对卡箍直管系统有限元模型中卡箍的水平、竖直刚度进行修正，辨识卡箍在各个拧紧力矩下的水平、竖直刚度，如表6所示。

表6 卡箍在不同拧紧力矩下的刚度参数

修正后卡箍直管系统在各个拧紧力矩下的模态分析结果与试验结果对比如表7所示。

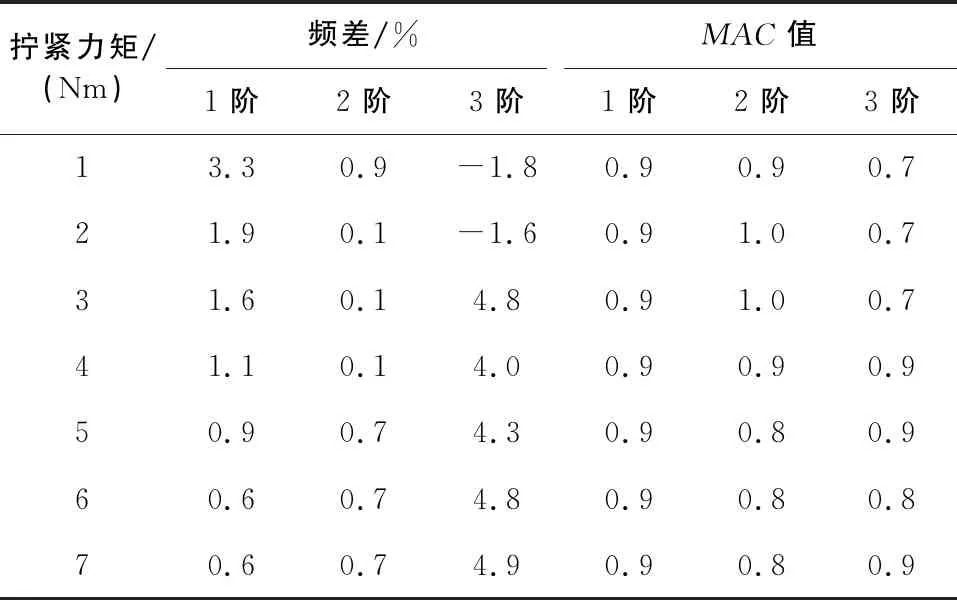
表7 修正后卡箍直管系统的模态分析结果与试验结果对比

修正后卡箍直管系统有限元模型在各个拧紧力矩下的模态分析结果与试验结果的最大频差为4.87%。除了1～3 Nm拧紧力矩下的第3阶模态振型的MAC值较低，其余MAC值都在0.8以上，这说明修正后的卡箍刚度参数可以反映实际卡箍在各个拧紧力矩下的刚度特性。

通过表6可以得到卡箍水平、竖直刚度与拧紧力矩的函数关系，分别如式(3)、式(4)所示。

(3)

(4)

式中：kshuiping为卡箍水平刚度；kshuzhi为卡箍竖直刚度；M为拧紧力矩。

3 卡箍位置对管路系统特性影响

3.1 卡箍位置对管路系统特性影响的试验研究

分别将图2中卡箍向左平移到距离管路右端80 mm、120 mm、160 mm、200 mm、240 mm、280 mm的位置，重复卡箍直管系统在不同拧紧力矩下的模态试验，得到将卡箍置于不同位置处直管系统在不同拧紧力矩下的水平、竖直基频，从而建立简单直管系统水平、竖直基频与卡箍位置关系曲线，如图6所示(本刊系黑白印刷，有疑问之处可咨询作者)。

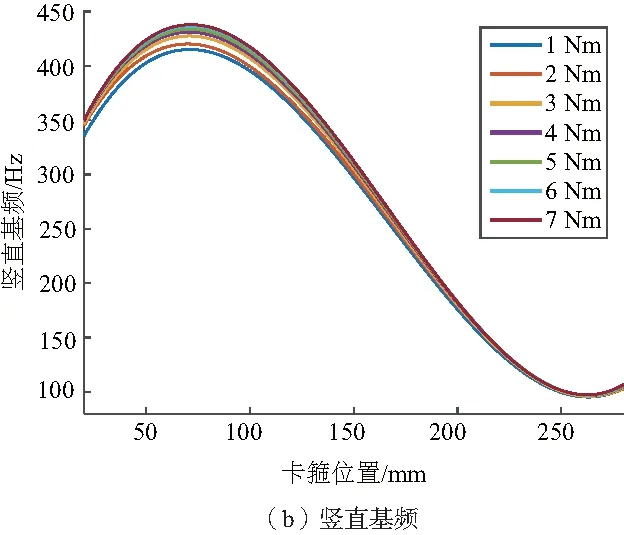
图6 卡箍直管系统水平、竖直基频与卡箍位置的关系

随着卡箍向左端固支处接近，卡箍直管系统在不同拧紧力矩下的水平、竖直方向的基频都是先增大后减小。当卡箍距离直管右端64.1 mm时，直管系统在各个拧紧力矩下的水平基频达到最大；当卡箍距离直管右端69.5 mm时，直管系统在各个拧紧力矩下的竖直基频达到最大。

3.2 卡箍位置对管路系统特性影响的仿真研究

基于2.3节得到的卡箍水平刚度、竖直刚度与拧紧力矩的关系，仿真不同卡箍位置的管路系统在不同拧紧力矩下的模态实验，得到不同卡箍位置的管路系统在不同拧紧力矩下的前2阶仿真频率，与试验结果对比如表8所示。

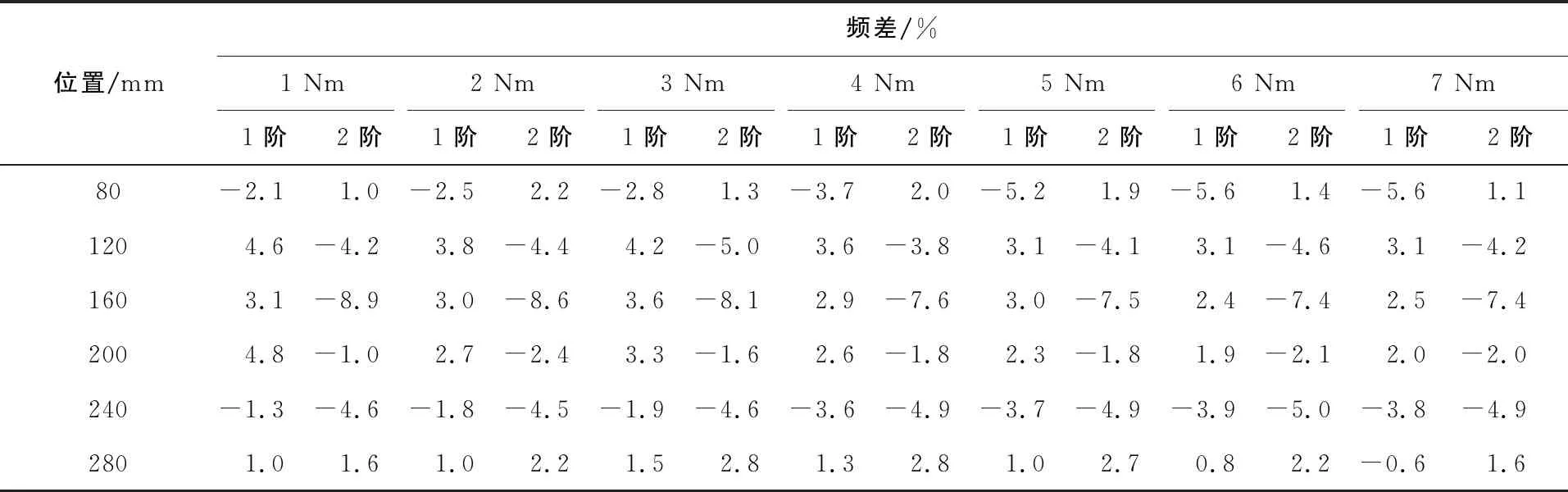
表8 不同卡箍位置管路系统在1～7 Nm拧紧力矩下的前2阶仿真频率与试验频率对比

水平方向基频的最大误差为-5.6%，竖直方向基频最大误差为-8.92%，绝对值都在10%以内，且绝大多数频差的绝对值都在5%以内。这说明2.3节得到的卡箍水平刚度、竖直刚度与拧紧力矩的函数在直管任何位置都适用。

4 结语

本文通过卡箍直管系统在不同拧紧力矩下的模态试验，建立了卡箍水平、竖直刚度与拧紧力矩的函数，并通过卡箍位置对管路系统特性影响的试验与仿真研究，验证了本文建立的卡箍水平、竖直刚度函数在直管任何位置都适用。本文的研究对管路系统的设计具有重要的指导意义，但是必须指出的是，本文结果建立在简单直管系统研究的基础之上，如果要推广到复杂管路系统，还需要做进一步研究。