高超声速飞行器助推段纵向姿态控制

张帅，盖科龙，黄筱莺

(南京航空航天大学 自动化学院，江苏 南京 211106)

0 引言

某高超声速飞行器利用火箭助推器内燃料产生的巨大推力将飞行器送入满足飞行任务的马赫数-高度窗口，然后分离火箭进入无动力运动模态。

高超声速飞行器的助推段纵向控制特有的难点：一是飞行速度和高度跨越范围大，气动特性差别大；二是助推发动机燃料消耗，飞行器在助推过程中有较大的质心变化，而质心变化将影响飞行器的稳定性和操纵性。

目前，对于高超声速无动力纵向控制方案的研究较多，但是对于助推段的纵向控制问题阐述得较少。因此本文将分析助推段的运动特性，并研究讨论两种纵向姿态控制方案的可行性，结合飞行器的任务给出助推段合理的纵向控制方案。

1 建模与对象特性分析

1.1 对象特性建模

高超声速飞行器助推段构型复杂，质量、惯量和质心随着助推发动机燃料的消耗实时变化；助推段飞行包线大，马赫数、高度变化剧烈，飞行器气动特性变化大。因此建立整个助推段飞行过程的六自由度仿真模型，需要对大气环境、地球模型以及飞行器自身的气动、执行机构、推力、质心、质量以及惯量进行建模分析。

基于作者所在实验室开发的“高超声速飞行器动力学通用模型库”架构，结合上述本文研究对象的特有属性，图1给出了助推段非线性数学模型搭建的整体框架图。其中u表示舵面的输入量，包括气动舵和燃气舵;y表示输出量，主要是迎角、侧滑角和马赫数。

图1 飞行器助推段非线性数学模型

1.2 对象特性分析

1) 纵向静稳定性分析

飞行器纵向静稳定性主要是指飞行器的气动焦点与质心之间相对关系，纵向静稳定性导数可以表示为：

(1)

图2给出了飞行器的助推段不同马赫数下纵向静稳定导数随迎角的变化曲线。可以看出，在马赫数从0.4～6.5的过程中，纵向静不稳定，且马赫数越小，纵向静稳定导数越大；即静不稳定的程度越大；同时马赫数越大，静不稳定导数越小，在一定程度上提高了静稳定性。

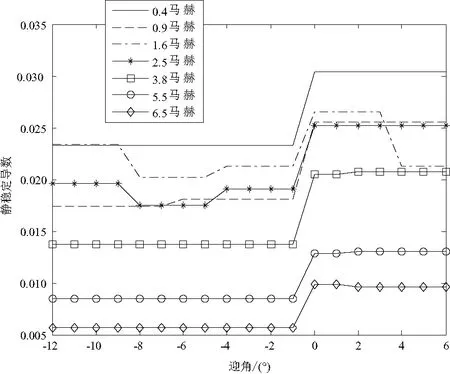
图2 纵向静稳定导数曲线

2) 模态特性分析

飞行器的纵向模态通常由短周期模态和长周期模态组成，分别对应纵向运动状态方程的极点，即一对大共轭复根和小共轭复根。纵向静不稳的飞行器其短周期模态特征根退化为一个实根和一个带有短周期阻尼比，周期类似于长周期运动的新振荡模态，称为第三振荡模态[1-2]。

沿着高度-马赫数标称轨迹剖面，固定迎角-4°，选取覆盖整个助推段的特征点进行配平和小扰动线性化，根据每个状态点的纵向特征根分布定性分析飞行器在助推段的动稳定性。

由表1可知，由于纵向静稳定导数>0，助推段整个飞行过程中都存在由短周期模态特征根退化而来的正实根。随着马赫数增大，飞行器燃料消耗，质心前移，纵向静稳定导数变小；动压的变化趋势是先随着速度增大而快速增大，后随着大气密度减小又减小[3]。从表1中可以看出，正实根数值大小的变化趋势是随着马赫数增大而减小，说明助推段内纵向动态发散的趋势主要由纵向静不稳定特性导致的，而高速使得正实根的数值变大，加剧了快速发散的特性。

表1 助推段纵向特征根

2 纵向控制策略

飞行器助推段的控制系统总体结构图如图3所示。首先根据飞行任务和飞行器自身飞行约束生成轨迹参数，即纵向制导指令和纵向控制指令，然后对纵向制导回路进行高精度的高度和高度下沉率跟踪，生成纵向控制指令的修正量，最后由姿态内回路实现对控制指令的响应。

图3 助推段控制系统总体结构图

本文主要讨论助推段的控制律，因此不解释轨迹和制导律的设计过程。纵向姿态控制若采用迎角控制和俯仰角控制都可以起到增稳的作用，下面将比较迎角反馈控制律和俯仰角反馈控制律下助推段控制系统的稳定性和完成飞行任务的能力[4]。

迎角控制律如式(2)所示，俯仰角控制律如式(3)所示。其中：δe为升降舵；α为迎角；αc迎角指令；θ为俯仰角；θc为俯仰角指令；q为俯仰角速率；Kα、Kθ为PID参数。

(2)

(3)

3 迎角控制回路

3.1 开环特性分析

1) 根轨迹分析

在助推段标称轨迹上选取状态点(马赫数为2，高度为8 582m，迎角为-4°)配平线性化，得到迎角到升降舵的传递函数为：

(4)

其中包含不稳定极点5.639。

对于本文的研究对象，助推段的增稳控制是控制系统设计考虑的首要环节。

根据控制律公式(2)，给出根轨迹示意图。可见，首先角速率反馈和迎角反馈影响了负极点和共轭极点的轨迹，其次随着反馈增益Kα增大，正实根的轨迹不变，仍然向着较小的正零点移动，因此始终存在的正零点决定了迎角反馈回路中长周期无法稳定的闭环特性(图4)。

图4 Δα(s)/Δδe(s)反馈根轨迹示意图

2) 频率特性分析

图5给出了迎角到升降舵的开环频率幅值曲线和相位曲线。可见，迎角到升降舵的低频增益很小，意味该单输入单输出系统不具有良好的命令跟踪性能和良好的低频干扰衰减性能。

图5 Δα(s)/Δδe(s)开环频率特性

总结以上讨论，迎角到升降舵回路中由于存在右半平面零点，导致右半平面的极点始终无法被拉回左半平面。而右半平面极点和零点将严重限制系统可获得的性能[5]。系统的极点取决于该系统固有的动态特征方程，由线性系统动态方程的特征矩阵A的特征值确定，改变极点的唯一方法是重新设计飞行器气动结构；系统的零点取决于传感器、发动机是如何与状态耦合的，在线性系统中，零点由所有的矩阵A、B、C和D决定[6]。因此，零点可因选择使用新的传感器信息而改变，这也是本文讨论控制变量使用迎角还是俯仰角的重要意义。

3.2 轨迹灵敏性分析

飞行器纵向二维质点运动方程如式(5)所示。可见迎角不仅仅是用来产生气动力，还用来产生发动机推力T沿轨迹线方向的分量Tn=Tsinα，在Tn的作用下控制H-V轨迹[7]。

(5)

当飞行速度到马赫数为2时接入迎角控制，给出迎角指令-1°～-5°[8]。图6给出了不同迎角下飞出的高度-马赫数轨迹曲线，可见：

1) 迎角控制下，迎角小范围波动就会引起高度较大变化。

2) 在马赫数为4进入窗口时，迎角-3°的高度曲线在窗口上边界，迎角-4°的高度曲线在窗口下边界，进入窗口的迎角裕量只有1°，进入窗口较难。

由此可得，迎角控制下高度轨迹对于迎角的敏感性太强，若实际飞行中不确定性对迎角有所干扰，极易导致轨迹偏离无法完成飞行任务。

图6 迎角控制下高度-马赫数曲线

4 俯仰角控制回路

4.1 开环特性分析

1)根轨迹分析

在助推段标称轨迹上选取状态点(马赫数为2，高度为8 582m，迎角为-4°)配平线性化，得到俯仰角到升降舵的传递函数为：

(6)

与迎角到升降舵的传递函数相比，未出现右半平面的零点，极点相同。

根据控制律式(3)，给出俯仰角到升降舵的根轨迹示意图。可见随着增益Kθ增大，正实根向左半平面移动先形成负实部绝对值较小的共轭极点，后可变成负实部绝对值较大的共轭极点(图7)。

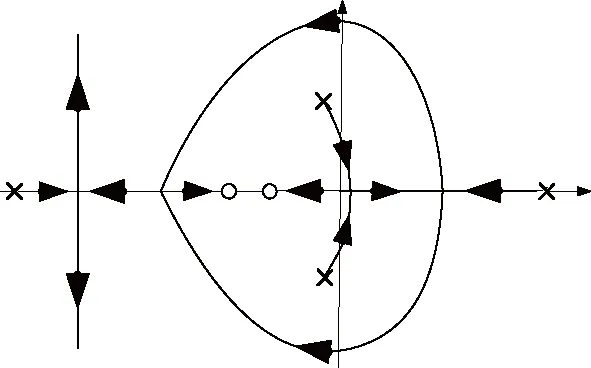
图7 Δθ(s)/Δδe(s)反馈根轨迹示意图

2)频率特性分析

图8给出了俯仰角到升降舵的开环频率幅值曲线和相位曲线。可见，相比于迎角，俯仰角到升降舵的低频开环增益较大，大约是10倍，表示俯仰角反馈系统具有良好的命令跟踪性能和良好的低频干扰衰减性能；在中频段，俯仰角反馈和迎角反馈一样，幅值均较小，动态特性差，需要调节合理的增益参数改善动态特性。

图8 Δθ(s)/Δδe(s)开环频率特性

4.2 轨迹灵敏性分析

(7)

助推段纵向全程采用俯仰角控制，给出7条俯仰角指令轨迹，分别为标称俯仰角剖面和将其上下平移-5°～1°的俯仰角剖面。图9给出了跟踪各俯仰角剖面飞出的高度-马赫数轨迹曲线，可见：

1)相比于迎角控制，俯仰角小范围内波动不会引起高度较大的变化。

2)在马赫数为4进入窗口时，俯仰角变化6°范围内的高度都在窗口高度边界内，进入窗口较易。

由此可得，俯仰角控制下高度轨迹对于俯仰角的敏感性较弱，拥有容忍俯仰角偏差完成飞行任务的能力。

5 结语

本文着重研究助推段迎角反馈控制律和俯仰角反馈控制律的可行性问题。首先给出了特性分析方法和结果，发现飞行器在火箭助推段纵向静不稳定程度较大，因此增稳纵向模态是纵向控制的基础。在此基础上，本文给出了反馈迎角加俯仰角速率和反馈俯仰角加俯仰角速率的增稳策略，通过根轨迹及物理概念解释了两种增稳策略的差异；再结合研究对象助推段的飞行任务，给出了两种控制律完成飞行任务的能力分析。最终结合多方面的分析比较，确定控俯仰角作为高超声速飞行器助推段的控制律是更为有效、合理的纵向控制策略。

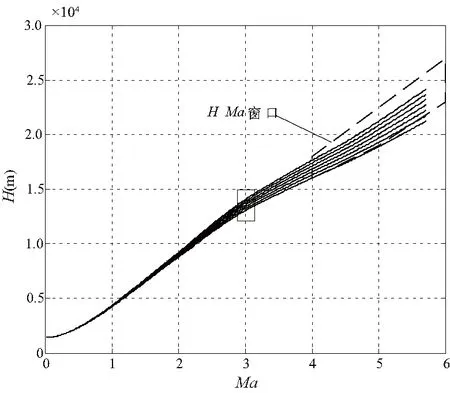
图9 俯仰角控制下高度-马赫数曲线