一种饮料包装并联机械手设计与分析

王鹏，王莹，王晋鹏，李阿为，惠虎静，郗梦璐

(西安航空学院 机械工程学院，陕西 西安 710077)

0 引言

近年来，我国并联机器人应用日益广泛，在国际上也备受关注。与串联机械手相比，并联机械手具有刚度大、载荷大、位置精度高、结构紧凑等优点，特别适合于工作空间小或负载量小的应用环境[1]。大多数并联机械手应用于重工业，例如：梁宏宝教授将五自由度移动机械手用于石油工业的管道修补领域[2]。但在轻工业尤其在包装行业应用较少。因此，开发一种应用于饮料包装自动生产线的并联机械手是非常有必要的。

李雪鹏基于一种六杆闭环结构，提出了两种新型含平面六杆闭环分支的六自由度并联机构，并进行了奇异性分析[3]；黄田教授领衔的研究团队发明的一种“Diamond机构”的高速并联机器人，突破了“几何精度保障、高速平稳控制、作业装备布局、物料视觉跟踪、抓取路径规划”等五个关键核心问题[4]；王冰等人设计了一种可实现末端运动平台平动并且具有较小运动惯量的平面二自由度并联机器人[5]。WAHLE M在Delta并联机构运动学逆解算法的基础上，在并联机构的静力学分析方面取得了瞩目的成果，推导出了该种并联机构的刚度矩阵[6]；在并联机构冗余驱动的研究方向，M.A.Nahon，T.Ropponen等人提出了冗余驱动主要是利用对驱动力进行协调分配，从而取得并联机构在能量损耗、内力等性能指标得到优化等论断的众多成果[7]。

虽然上述设计方法对并联机械手的进行运动学分析，但是主要针对高速重载情况下的并联机械手。为了解决罐装饮品智能生产线上生产效率低的问题，本文将并联机械手应用于饮料包装自动生产线，根据机构平面平动设计原理，设计一种并联机械手。依据机构运动学位置正逆解原理，对机械手的运动进行理论分析。利用图解法求出并分析了机械手末端执行手爪的工作空间。

1 并联机械手结构设计

为了实现并联机构运动，连接动平台和支链的运动副必须是转动副，并且至少在1条主动支链或从动支链中，由1个动平台和其他3个运动杆件所构成的平行四边形，相互之间必须经转动副连接且动平台上的边与机架上固定边始终保持平行，可以实现两自由度并联机构平面平动且始终作平面运动[8]。如图1所示，动平台上的边AB与机架上固定边CD必须满足相互平行的关系。

图1 动平台作平动的必要条件简图

根据并联机械手总体结构的设计原则和基本部件设计尺寸，机械手作业场合的其他条件约束，通过Pro/E5.0进行三维设计，该饮料包装并联机械手三维模型，如图2所示。

图2 并联机械手三维模型

2 运动学分析

并联机构采用左右对称且主、从动臂分别等长同构型，作为末端执行器的机械手手爪运动为一刚体的平动，可以在运动学将原机构(图3)简化为五杆铰接机构，如图4所示，进而对本并联机械手的机构进行位置理论分析更加方便。

图3 并联机械手机构简图

图4 并联机械手五杆铰接机构

选取机架上两电机间距的中点为竖直平面直角坐标系的坐标原点O，建立坐标系xOy，如图5所示。设固定平台、主动臂、从动臂的位置分别为矢量r=(x,y)T、l1ui、l2wi，主动臂(机械手小臂)与从动杆(机械手大臂)的转角分别用θ1i、θ2i表示，其中有:

其中ui(cosθ1i,sinθ1i)与wi(cosθ2i,sinθ2i)分别为主动臂和从动臂的单位矢量[9-10]。

图5 机构运动学分析简图及参数

位置逆解分析是机构运动学分析的理论基础，用已知动平台上参考点θ’的位矢r，来确定主动臂转角θ1i(i=1,2)。在直角坐标参考系xOy下构造闭环方程：

r-sgn(i)ee1-l1ui=l2wi,i=1,2

(1)

式中:l1、l2，ui，wi分别表示两条链i中主、从动臂板件的长度和单位矢量；e表示电机轴线间距与动平台上两铰间距之差，即前面提到的相对距离。

以上各参数可分别表示为：

ui=(cosθ1i,sinθ1i)T

wi=(cosθ2i,sinθ2i)T

e1=(1,0)T

在式(1)两端同时乘以各自的转置，有：

即可得到r与ui之间的关系：

x2+y2+e2+l12-l22-2sgn(i)erTe1-

(2)

由上式整理得到一个三角方程：

Aisinθ1i+Bicosθ1i+Ci=0

(3)

式中：

Ai=-2l1y

Bi=-2l1(x-sgn(i)e)

(Ci-Bi)ZiT+2AiZi+(Ci+Bi)=0

(4)

由机构的装配模式得：

(5)

故得：

(6)

据此，可确定ui及由下式解出：

(7)

3 运动仿真

从简图原理分析其类似于一个五杆铰接机构，其中2台伺服电机固定于工作台面上，机械手主、从动臂以转动副的方式铰接形成整个机构,如图6所示。本文运用Adams2016软件对并联机械手进行工作空间运动范围的仿真分析[11]。

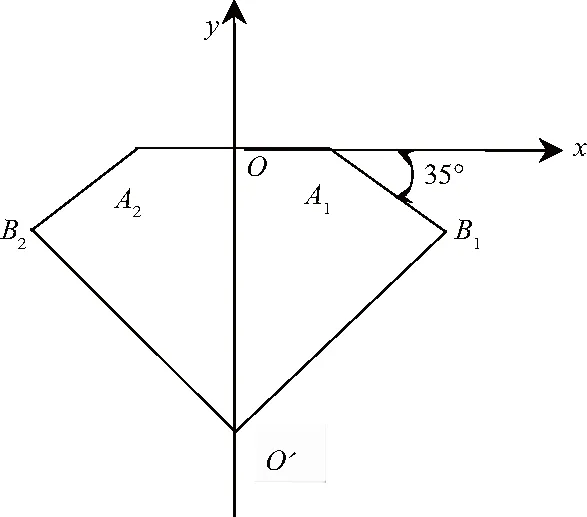
图6 并联机械手初始状态位置图

由图6可知，并联机械手初始状态时右端主动臂与x轴间夹角为35°，设θ11为50°，θ为160°，同时控制2台伺服交流电机以同转速、同方向开始运行，当右端机械手小臂分别逆向运行至85°和顺向运行至75°时，让其机构停止运动，此时所转动的度数满足所设θ11和θ的要求。根据两次机构末端O′的位置轨迹，验证机构的工作空间运动范围是否可行。

根据并联机械手结构基本设计尺寸，得表1所示的初始位置坐标。

表1 并联机械手各铰接点初始坐标表

绘制板件链接，附转动副于各铰接点，然后给A1、A2处加上旋转驱动，如图7所示。

图7 机构仿真初始位置以及驱动施加图

据θ=ωt和ω=2πn，设置2台电机转动的角速度和仿真时间参数，经运算：逆转85°时，仿真时间约为0.008 s；顺转75°时，仿真时间约为0.007 s。

机构运动仿真如图8所示。

图8 机构运动仿真图

利用Adams2016对该机构进行运动仿真，让机构从初始位置分别逆向、顺向转动满足相应要求的角度，在逆向、顺向运动仿真的两个过程中得到了末端端点O′(并联机械手手爪安装处)的位移曲线图，见图9和图10。

图9 机构逆向运动仿真过程中O′的位移曲线图

图10 机构顺向运动仿真过程中O′的位移曲线图

因此，证实并联机械手手爪运动范围与理论分析保持一致。

4 结语

针对目前易拉罐罐装饮品智能生产线上生产效率的问题，提出并设计了一种在一定的平面范围内自由移动的并联机械手。运用两自由度并联机构平面平动设计原理，完成了并联机械手总体结构设计，对各零部件进行了三维建模，并对其进行运动仿真和仿真验证。通过运动仿真表明：该并联机械手手爪运动范围与理论分析保持一致，为并联机械手运动的研究提供了一定的理论基础。