“平面直角坐标系”考点集卒

吴行民

“平面直角坐标系”的有关概念，蕴涵的思想方法，以及在实际生活中的广泛应用，都是中考试题常常涉及的，请看吴老师给同学们搜集来的“平面直角坐标系”的考点，

考点1：确定已知点所在的角限

例1 （2019年株洲）在平面直角坐标系中，点A（2，-3）位于（    ）象限.

A.第一

B.第二

C.第三

D.第四

分析：建立了平面直角坐标系以后，坐标平面就被两条坐标轴分成四个区域，从右上方区域开始，按逆时针方向依次叫作第一象限、第二象限、第三象限、第四象限.各象限内点的坐标符号是：第一象限内点的横、纵坐标皆为正数，即（+，+）;第二象限内点的横坐标为负数，纵坐標为正数，即（一，+）;第三象限内点的横、纵坐标皆为负数，即（一，一）;第四象限内点的横坐标为正数，纵坐标为负数，即（+，一）.

解法1：先在x轴上找出表示2的点，再在，，轴上找出表示-3的点，过这两个点分别作x轴和y轴的垂线，垂线的交点就是点A（2，-3），显然它在第四象限，故选D.

解法2：因为点A（2，-3）的横坐标是正数，纵坐标是负数，所以点A（2，-3）在第四象限.故选D.

点评：理解并熟记各象限内点的坐标的符号特征，是解决这类问题的关键.

考点2：建立坐标系确定的坐标

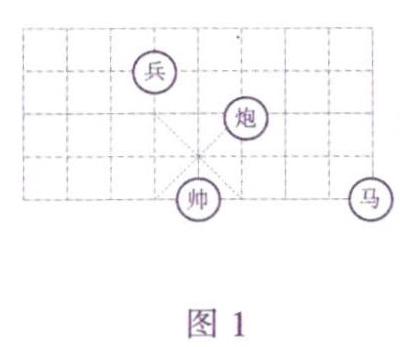
例2 （2019年陇南）中国象棋是中华民族的文化瑰宝，因趣味性强，深受大众喜爱.如图1，若在象棋棋盘（部分）上建立平面直角坐标系，使“帅”位于点（0，-2）处，“马”位于点（4，-2）处，则“兵”位于点一 处，

分析：直接利用“帅”位于点（o，-2）处和“马”位于点（4，一2）处，可以确定原点的位置，进而建立平面直角坐标系.于是可以得出“兵”所在位置的坐标，

解：根据题意，可以建立如图2所示的平面直角坐标系，故“兵”位于点（一1，1）处.

点评：本题考查了平面直角坐标系的建立和点的坐标的确定，解题的关键是确定平面直角坐标系中原点的位置，

练一练

（2019年黄冈）已知点A的坐标为（2，1），将点A向下平移4个单位长度，得到的点A的坐标是（   ）.

A.（6，1）

B.（-2，1）

C.（2，5）

D.（2，-3）

参考答案：D