拓展分析 归纳方法
张丹
同学们要善于在解题后进行反思,把解题过程中发现的规律或结论,进行拓展,归纳出深层次的方法或经验.这样不仅有利于今后解题时自我指导,还能在拓展的过程中巩固所学知识,感受数学魅力.并且在潜移默化中提升自己的数学素养.张老师以一道课本习题为例,抛砖引玉,希望能给同学们一些帮助,
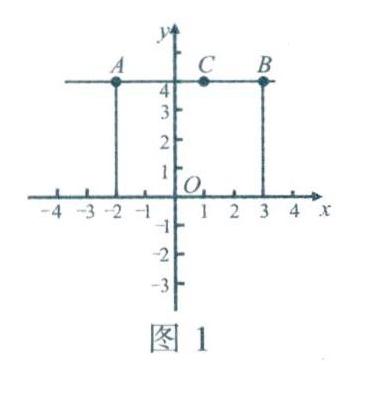
例1 (人教版数学教科书七年级下册第70页第8题)建立一个平面直角坐标系,描出点A (-2,4),B(3,4),画直线AB.若点C为直线AB上任意一点,则点C的纵坐标是什么?想一想:
(1)如果一些点在平行于x轴的直线上,那么这些点的纵坐标有什么特点?
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标有什么特点?
解析:如图1所示,直线AB即为所求,若点C为直线AB上任意一点,则点C的纵坐标是4.由此可以归纳出如下一般性结论:
(1)如果一些点在平行于x轴的直线上,那么这些点的纵坐标都相等;
(2)如果一些点在平行于y轴的直线上,那么这些点的横坐标都相等.
【反思l】回顾上述问题解答过程,逆向思考:在平面直角坐标系中,如果两个点的纵坐标相等且不等于0,那么这两点确定的直线与x轴平行吗?如果两个点的横坐标相等且不等于0,那么这两点确定的直线与y轴平行吗?
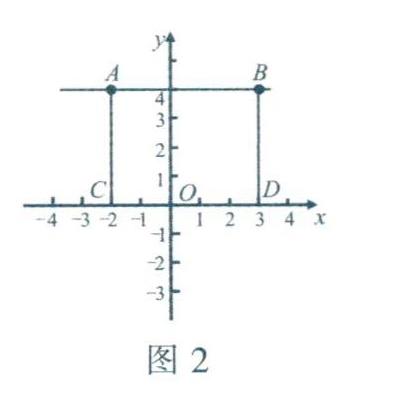
如图2,设点A (xi,y),B(X2,y),其中x1≠x2,y≠0.分别过点A.B作x轴的垂线,垂足分别是点C,D,则∠ACD=∠BDC=90°,故AC//BD.
又因为AC=BD= |y| >0,所以线段BD可以看成是由线段AC平移得到的,所以4B//CD,即AB//x轴.
同理,可以证明:若点M(x,Yi),N(x,y2),其中y1≠y2,x≠O,则MN//y轴.
于是我们归纳得到如下结论:在平面直角坐标系中,如果两个点的纵坐标相等且不为0,那么这两点确定的直线与x轴平行;同样地,如果两个点的横坐标相等且不为0,那么这两点确定的直线与y轴平行.
【反思2】回顾上面的分析过程,想一想,在AC=BD= |y| >0中,为什么要把坐标y加上“绝对值”?
理解这一点并不难,因为这里AC,BD表示线段的长度,而坐标y描述“有方向的量”,是一个赋予“+”或“一”属性的数,根据绝对值的定义,|y|正好表示平面直角坐标系中的点到x轴的距离.对此,我们强调,凡是用坐标表示相关线段的长度,一定要加上绝对值符号,防止漏解,而且加上绝对值符号,进而参与运算,可以回避分类讨论带来的麻烦,
例2在平面直角坐标系中,已知点A(m-2,0),B(0,4-2m),若S△ABO=9,求点A,B的坐标.
解析:根据题意得AO= |m-2|,BO=|4-2m|=2|m-2|.
所以.S△ABO=1/2AOxBO= 1/2|m-2|×2|m-2|=|m-2|2,故|m-2|2=9,即(m-2)2=9.
解得m=5或m=-1.故点A.B的坐标可分别为(3,0),(0,-6),也可分别为(-3,0),(0,6).
【反思3】数轴上表示数a,b的两个点A,B,它们之间的距离可以表示为AB=|a-b|.把这个规律拓展到平面直角坐标系中,得到:x轴上或平行于x轴的直线上两个点A (x1,y),B(x2,y),其中XI≠X2,它们之间的距离可以表示为AB= |x2-x1|;同样,),轴上或平行于y軸的直线上两个点C(x,y1),D(x,y2),其中y1≠y2,它们之间的距离可以表示为CD=|y2-y1|.运用此结论,可给我们解决相关问题带来方便,
例3在平面直角坐标系中,已知点A (-2,4),B(3,4),C(m,4),若A C=2AB,求m的值.
解析1:AB=3-(-2)=5,当点C在点A的左侧时,与上面分析相同,得AC=-2-m=10,解得m=-12.当点C在线段AB上时,AC不可能等于AB.当点C在点B的右侧时,AC=m+2=10,解得m=8,符合题意,故m的值为-12或8.
解析2:AB=3一(一2)=5,因为点A(-2,4),B(3,4),C(m,4),所以点A,B,C在同一条平行于x轴的直线上.
而AC= |m-(-2)|=|m+2|,由已知得|m+2|=2x5,解得m=-12或m=8.
故m的值为-12或8.
【反思4】比较上面两种解法,显而易见,方法2引用绝对值符号,思路更清晰,过程更简捷,回避了分类讨论,减少了解题错误发生率.
例4在平面直角坐标系中,已知点A (-2,4),B(3,4),C(1,1),D(1,m),若A ,B,C,D四点构成的图形的面积是10.求m的值,
解析:如图3,因为点A (-2,4),B(3,4),所以AB//x轴,且AB=3-(-2)=5.
又因为点C(1,1),D(1,m),所以CD∥y轴,且CD=|m-1 1|.
易证AB⊥CD,所以A,B,C,D四点构成的四边形的面积等于1/2AB×CD,所以5/2|m-11=
10.解得m=5或m=-3.
练一练
1.已知点A(2,m2),B(m,4),则当m=时,AB//x轴.
2.已知点A(2,2m+1),B(2,m+3),若AB=5,则m=
一.
3.已知点A(2,2m+1),B(3,4),C(2,3),D(-1,-1),若A,B,C,D四点构成的四边形面积等于12,则m=____.
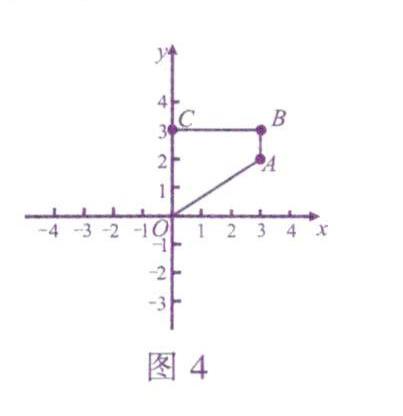
4如图4,已知点B(5-2m,n),A(2m+1,n-1),C(O,3),若AB //OC,则四边形ABCO的面积等于
.
参考答案:1.-22.7或-3 3.4或-2 4.6

