外接球和内切球半径的求解策略

童其林

（龙岩市永定区城关中学，福建 龙岩 364100）

所谓多面体的外接球，是指这个多面体的各个顶点都在这个球的表面上；所谓多面体的内切球，是指这个球和多面体的每个面都相切，即这个球和多面体的每个面有且只有一个公共点.多面体的外接球和内切球是立体几何的重要内容，也是一个热点、难点内容.解决此类问题，需要有较强的空间想象能力，需要找出球心，求出半径，还需要一番推理论证，因而不少学生望而生畏，束手无策.本文先通过认识几种特殊多面体的外接球和内切球的半径的求法，再通过具体实例得到此类问题的求解策略，并形成教学启示.

一、几种特殊多面体的外接球和内切球的半径

如长方体的外接球，正方体的外接球和内球球，正三棱柱的外接球，正三棱锥的外接球和内切球，正四面体的外接球和内切球等都是常见的模型.

1.长方体的外接球

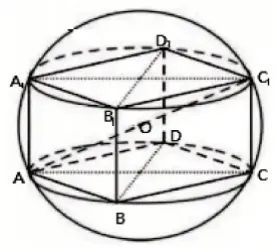
图1

2.正方体的外接球和内球球

3.正三棱柱的外接球

设正三棱柱ABC-A1B1C1的高为h,底面边长为a,如图2，D 和D1分别为上下底面的中心，则球心必落在高DD1的中点O 上，

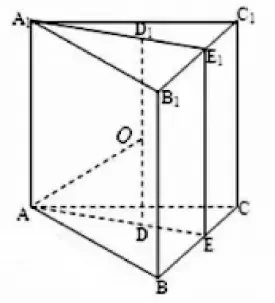
图2

4.对棱相等的三棱锥（等腰四面体）的外接球

对棱相等的三棱锥（等腰四面体）S-ABC 中，SA=BC=a,SC=AB=b,SB=AC=c,则三棱锥S-ABC外接球半径R=

证明：构造长方体（如图3），则三棱锥的外接球就是长方体的外接球.设长方体的长宽高分别为x,y,z,外接球半径为R，则

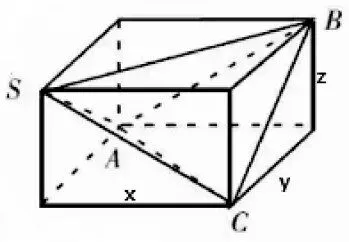
图3

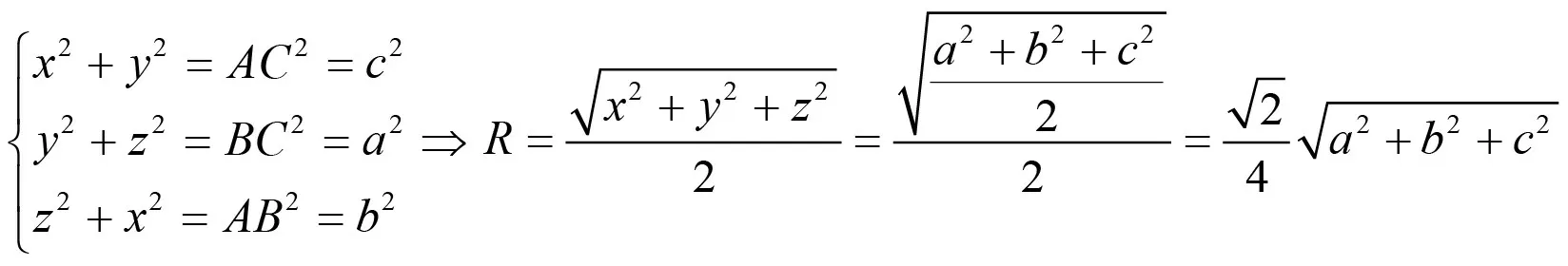
5.四个面都是直角三角形的三棱锥的外接球

四个面都是直角三角形的三棱锥P-ABC 中，PA⊥平面ABC，AB⊥BC,PA=a,AB=b,BC=c,则三棱锥P-ABC外接球的半径

证明：可构造长方体（如图4），则三棱锥的外接球就是长方体的外接球，所以

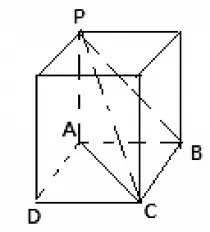
图4

6.正三棱锥的外接球和内切球

证明：如图5，设正三角形ABC 的中心为H，连接SH,AH,由正三棱锥知SH⊥平面ABC，设外接球的球心为O，半径为R，则球心O 在SH 上，连接OA,则

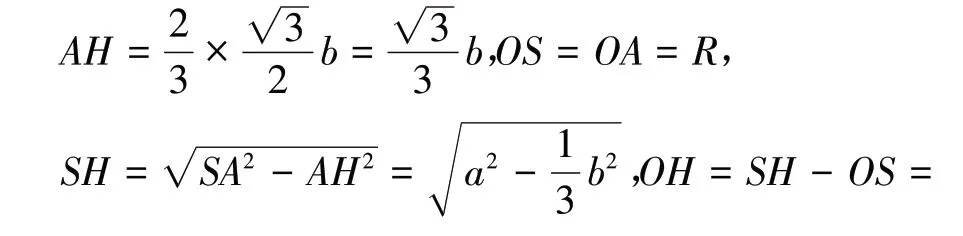
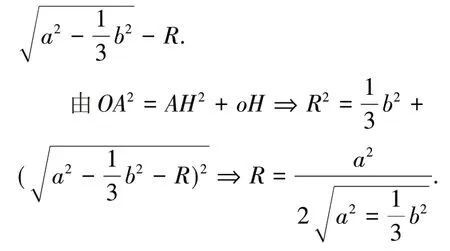
图5

如图6，设斜高PD=h′，三棱锥的高PH=h,则

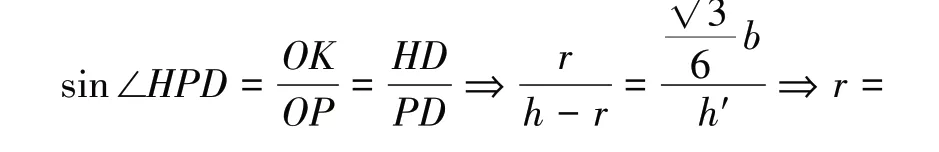
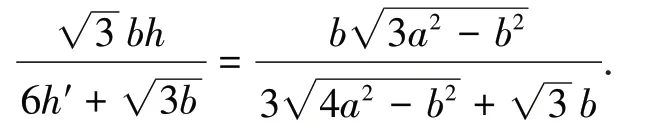
图6

7.正四面体的外接球和内切球

令b=a，则可得正四面体外接球半径R=，内球球半径

另证1：连接内球球球心与各顶点，把三棱锥分成四个小三棱锥，由等体积法得

另证3：如图7，将正四面体补形为正方体，正四面体棱长为a,则正方形边长，所以

点评：多面体的内切球方法一:做过棱及球心的截面，求多边形的内切圆半径即为内切球的半径.方法二，等体积法:把球心和各顶点连接构成以球心为顶点的n个小棱锥的体积和等于这个多面体的体积，小棱锥的高就是内切球半径.

图7

8.三棱锥中有两个面为共斜边的直角三角形的外接球

三棱锥P-ABC中，设 BA=a,BC=b，BA⊥BC，PA⊥PC,则其外接球半径

证明：将三棱锥P-ABC 补形为长方体（如图8），则三棱锥的外接球就是长方体的外接球的球心.

图8

另证：因为直角三角形斜边的中点到三角形各顶点距离相等，所以AC 中点即为三棱锥外接球的球心，AC 长就是直径，所以

9.三条侧棱两两垂直的三棱锥（墙角模型）的外接球

如图9，三棱锥S-ABC 的三条侧棱SA,SB,SC 两两垂直，且SA=a,SB=b,SC=c,则其外接球的半径R=

图9

二、外接球和内切球半径的求解策略

1.补形法求三棱锥球半径

割补法是解决有关立体几何问题的常用方法，如求体积，证明线线、线面、面面平行或垂直，当然也是解决一些外接球和内切球的有效方法.

例1 如图10，在三棱锥D-ABC 中，DB⊥平面ABC,,求三棱锥DABC外接球半径R.

解析：将三棱锥补形为直三棱柱ABC-FDE,则三棱锥的外接球就是直三棱柱外接球的球心（如图11）.设△ABC，△DEF是外接球的球心分别为O1，O2,连接O1O2，则直三棱柱外接球的球心就是线段O1O2的中点O,连接OC,O1C.

图10

在△ABC中，由正弦定理得=1,所以R2=

图11

点评：也可以通过找三棱锥的球心得出半径.

2.定义法求外接球半径

定义是揭示概念内涵的逻辑方法，定义本身就是方法，而且是最本质的方法.

例2 已知平面四边形ABCD 中，AB=3，AD=4，BD=5，,BD⊥CD,如图12 是平面四边形ABCD 沿对角线BD 折成的四面体ABCD，且平面ABD⊥平面BCD，若四面体ABCD 的顶点在同一球面上，求该球的半径.

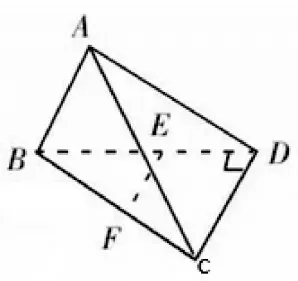
图12

解析：因为平面ABD⊥平面BCD，BD⊥CD，所以CD⊥平面ABD，所以CD⊥AD.因为,BD=5，AD=4，所 以BC=6，AC=，又AB=3，所以BC2=AB2+AC2，所以BA⊥AC.

取BC 的中点F,则F 为直角△BDC和直角△BAC斜边BC 的中点，所以，即F 到A,B,C,D 四个顶点的距离相等，故F 为球心，半径R=3.

点评：平面几何性质的应用为我们打开了一扇窗.

例3 三棱锥P ABC 中，PA⊥平面ABC 且PA＝4，△ABC 是边长为的等边三角形，则该三棱锥外接球的表面积为______.

解析：如图13，设D 为△ABC外接圆的圆心，则，过D 作DO⊥平面ABC,因为PA⊥平面ABC，所以PA 与OD 平行，取PA 中点E,过E 作EO 平行于DA,则O 为三棱锥P ABC 的球心，其半径为,外接球的表面积为4πR2=20π.

图13

点评：球心到各个顶点的距离相等，是我们思考的方向.

例4（2017 年福建省普通高中毕业班单科质量检查理科数学题）在三棱锥S-ABC 中，△ABC边长为3 的等边三角形，，二面角S-AB-C 的大小为120°，则此三棱锥的外接球的表面积为.

解析：如图14，因为SA2+AB2=3+9=12=SB2，所以三角形SAB 是以SB 为斜边的直角三角形，故斜边中点P 为三角形SAB 外接圆的圆心.

取底面的外接圆的圆心为Q，连接CQ 交AB 于D，连接PD，则D 为AB 的中点，从而DC⊥AB，

又PD平行于SA,故PD⊥AB，从而角PDC 为二面角S-AB-C 的大小,且∠PDC=120°,

图14

分别过P,Q 作垂直于平面SAB 与平面ABC 的垂线交于O，易知O 为该三棱锥外接球的球心，由PD=QD，可知PQ=OQ.

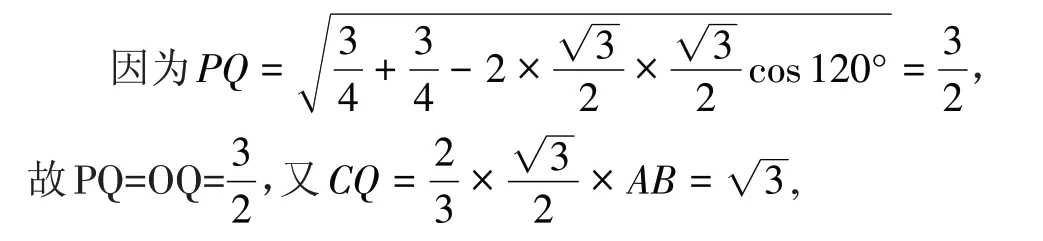
点评：三角形POQ 是等边三角形.

点评：本题是一个较为综合的问题，需要推理和运算同时进行，注意三角形POQ 是等边三角形.

3.方程法求外接球或内切球的半径

方程的作用是什么？求值.在有关给出数值的几何图形中，建立方程或方程组可求出外接球或内切球的半径.

例5（福州市2020 届高三理科数学5 月调研卷，理科16）已知三棱锥A-BCD的棱长均为6，其内有n个小球，球O1与三棱锥A-BCD的四个面都相切，球O2与三棱锥A-BCD的三个面和球O1都相切，如此类推，…，球ON与三棱锥ABCD的三 个 面 和 球ON-1都相切（n≥2，且n∈N*），则球01的体积等于______，球On的表面积等于________.

解析：如图15，AO是三棱 锥A-BCD的 高，O是△BCE的外心，因为三棱锥A-BCD的棱长均为6，则

图15

显然O1是三棱锥A-BCD的外接球和内切球的球心，O1在AO上，设外接球半径为R，内切球半径为r1，则由O1B2=OO12+BO2得，所以，所以

过AO中点作与底面BCD平行的平面与三条棱AB，AC，AD交于 点B1，C1，D1，则平 面B1C1D1与 球O1相切，由题意球O2是三棱锥A-B1C1D1的内切球，注意到三棱锥A-B1C1D1的棱长是三棱锥A-BCD棱长的所以有其内切球半径，同理，球On的半径为rn，则{rn}是公比为的等比数列，所以rn=r1×，所以

点评：求解三棱锥A-BCD的内切球体积，还可以用等体积法，解决第二问还需要较强的想象力和抽象概括能力.在一些看似困难，但容易建立空间直角坐标系的问题中，坐标法给了我们一条坦途.

比如，例1 也可以通过建立空间直角坐标系来完成.

4.等体积法求内切球的半径

例6（2020 届福州市高中毕业班第三次质量检查，理科12 题）三棱锥P-ABC中，顶点P在底面ABC的投影为△ABC的内心，三个侧面的面积分别为12,16,20，且底面面积为24，则三棱锥P-ABC的内切球的表面积为

解析：如图16，不妨设S△PBC=12，S△PAC=16，S△PAC=20,设P在底面ABC的投影为H，分别作HD⊥BC于点D，HE⊥AB于点E，HF⊥AC于 点F，则PD⊥BC.PE⊥AB,PF⊥AC,依题意，H为 △ABC的 内 心，则Rt△PDH≅Rt△PFH≅Rt△PEH，故PD=PF=PE，

图16

又

所 以S△PBC：S△PAC：S△PAB=BC：AC：AB=12：16：20=3：4：5，所以∠ACB=90°.

令BC=3x，AC=4x，AB=5x.

所 以，解得x=2，所以BC=6，AC=8，AB=10.

设△ABC内切圆半径为r，则AB)r=S△ABC，即，解得r=2，故HD=2.

所 以，

设三棱锥P-ABC的内切球的半径为R，则

点评：本题考查空间点、线、面位置关系，空间几何体的侧面积、体积等基本知识；考查空间想象能力、运算求解能力、论证推理能力；考查化归与转化思想；考查直观想象、数学运算等核心素养，体现基础性、创新性.

5.寻求轴截面

轴截面有其独特的性质，利用轴截面的性质又是求解外接球和内切球的半径的重要方法.

例7 正四棱锥S-ABCD的底面边长和各侧棱长都为，点S、A、B、C、D都在同一球面上，则此球的体积为____.

分析：正四棱锥S-ABCD的轴截面过球心，利用这一性质，可建立关于球半径的方程，得出半径R=1.

三、教学启示

球的内切和外接问题是人教版高中数学必修2 空间几何体的内容，后来在空间直角坐标系中也涉及，直到每一年几乎都有一道与简单多面体或旋转体有关的外接球和内切球问题，成为立体几何考查的热点、重点和难点.而确定外接球和内切球的球心和半径是解决此类问题的关键，所以研究其球心和半径的求解策略，及在教学中如何突破这一重点和难点就显得很有意义.

1.在必修课程涉及的空间几何体时就应重视外接球和内切球的教学

立体几何的学习，是从感性认识到理性认识的过程，其中的长方体的外接球是认识多面体外接球的开始，后来逐步认识正方体、正三棱锥、正四面体、正棱柱等特殊多面体的外接球和内切球，直到旋转体和不规则图形的外接球和内切球（假设外接球和内切球存在），这个过程是由浅入深、循序渐进的过程，是教学中应遵循的原则.在这个过程中，一方面要认识概念和定义，另一方面要进行解题训练，提高学生的空间想象能力，培养直观想象素养.体会立体几何的“直观感知，操作确认，思辨论证，度量计算”的过程.

需要注意的是，教材中这部分内容的练习不多，要加大这个练习力度，出好校本作业，让学生早点经历和体验外接球和内切球的内容.

2.在高三复习时要专题讲授和训练

这一阶段主要是对前期学习的一个总结和升华，揭示简单多面体和旋转体的的外接球和内切球球心位置和半径的特征，提高解决综合问题的能力.教学中，应通过一题多解，多题一解等方法提高学生运用知识的能力.

空间想象能力，是数学的关键能力之一，实现的载体是立体几何内容，而球的问题充满了想象、推理、论证和计算，可以通过历年高考题中涉及到简单多面体和旋转体的的外接球和内切球的问题进行专题讲授，获得相应的体验.

例8（2020 届福州市高中毕业班第三次质量检查，文科12 题）若圆锥的内切球（球面与圆锥的侧面以及底面都相切）的半径为1，当该圆锥体积取最小值时，该圆锥体积与其内切球体积比为

A.8:3 B.6:1 C.3:1 D.2:1

解法一：如图17，设圆锥底面半径为R，高为h.

由△apf∽△ace可得

因为h-2 > 0，所以，当且仅当，即h=4 时取等号，

所以该圆锥体积与其内切球体积比为2：1，故选D.

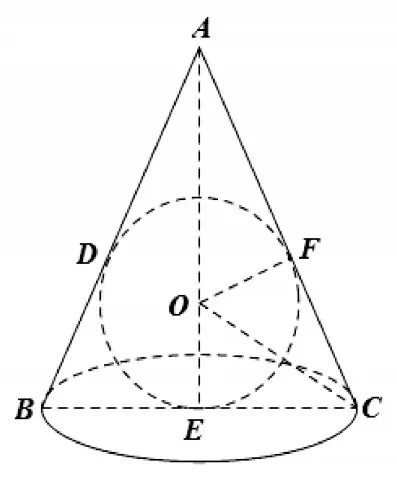
图17

所以f(h)在(2，4)上单调递减,在(4，+∞) 上单调递增,所以f(h)min=f(4)=8，

即h=4 时,该圆锥体积最小,最小值为又其内切球体积为

所以该圆锥体积与其内切球体积比为2：1，故选D.

点评：本文的例题主要是多面体外接球和内切球问题，其实旋转体的外接球和内切球问题也是重要的内容.