TransE和TransH模型空间地址表示学习中的对比研究——以广州市天河区为例

王 昕，李卫红*，童昊昕

(1． 华南师范大学地理科学学院，广州 510631； 2. 航天精一(广东)科技有限公司研究院，广州 510631)

地理信息的持续泛化已成为新地理信息时代的重要特征[1-2]，随着位置大数据的广泛应用，产生了海量诸如地址的位置大数据. 地址数据是泛化的地理数据，包括文字描述和位置描述，即语义地址信息和空间地址信息. 传统的地址实体表示方法可以分为2类：一是基于数字的经纬度定位方法，二是通过文本来对地址实体进行表示. 地址实体的文本表示实际上是地理编码问题，在这个信息化时代，如何使地址实体准确地被计算机理解并计算，这是至关重要的问题，大量学者对此进行研究[3-5]. 然而，地址实体不仅包含丰富的语义信息，也包含了大量空间信息，过分关注语义信息而忽略空间信息容易造成2种现象：一是地址实体语义相似而空间距离不相近；二是空间距离相近而地址实体语义不相似. 例如,华南师范大学和华东师范大学，一字之差却有1 400公里之远；百脑汇电脑城和中山大学附属第三医院相距不到一百米，字面上却毫无关联. 因此，如何将地址实体的语义信息与空间信息有效结合是解决上述问题的关键.

知识图谱[6-7]作为人工智能领域的研究热点，在知识的获取、表示、融合和推理上具有显著的特点. 随着卫星遥感与传感器技术的迅猛发展，大量基于位置的地理数据被人们获取与使用. 学者们将知识图谱技术引入到地理科学研究中：探讨地理知识图谱的构建与应用[8]、语料库的构建[9-11]、地理实体和关系的抽取[12-13]；实现地理学的“数据—信息—知识—智慧”的智能化转化[14]；使用知识增强技术，构建能够智能交互的虚拟地理环境服务框架[15]；借助知识嵌套技术，对包含时间和空间的轨迹数据进行知识表示，挖掘人们的日常习惯[16]；利用深度递归神经网络，对社交媒体数据进行地理实体的消歧工作[17]. 知识图谱技术的广泛应用，加速了海量地理数据向地理信息的转变，同时也为地理学者们扩展了地理学研究的新思路. 然而，知识图谱在本质上是一种结构化的语义网络，用来表示知识之间的相互联系，构建实体之间的关系网络，从而进行知识的相关计算，在这过程中对知识进行表示是知识图谱构建与应用的关键步骤[18]. 知识的表示学习[19]的目的是将知识库中实体和关系用低维的稠密向量来表示：在低维空间中，对象向量间距离越近则表示语义相似度越高，而对象向量间距离越远则表示语义相似度越低. 知识的表示学习能够高效计算实体与关系间的语义联系，量化对象之间的语义紧密程度，从而提高低频对象的精确性[20]. 然而，目前关于融合语义关系和空间关系的地址实体表示学习的研究较少.

为解决地址实体语义相似而空间距离不相近或空间距离相近而语义不相似的问题，本文运用知识的表示学习技术，将地址实体的语义信息和空间信息进行融合，通过实体间的向量距离来衡量地址的相似程度：以广州市天河区的标准地址数据为数据源，根据地址层级关系进行拆分，结合地址之间的空间关系和语义关系，构建空间地址三元组；运用表示学习模型TransE和TransH进行训练，将地址实体表示为低维的稠密向量，通过元组分类和实体间的向量距离来评估2个模型在地址表示学习中的优劣；最后分别比较地址实体的实际距离、语义相似度和实体间的向量距离. 本研究将有助于更精准地构建地理知识图谱，为地理知识图谱的表示学习提供方法借鉴，为地理信息科学在知识图谱领域的研究提供新的研究思路.

1 研究方法

1.1 TransE模型

2013年，BORDES等[21]提出了TransE模型，该模型基于实体和关系的分布式向量表示，其核心思想为：当(h，r，t)成立时应有h+r≈t(图1)，即将每个三元组实例(head，relation，tail)中的关系r看做从头实体向量h到尾实体向量t的翻译，通过不断调整h、r和t，使h+r尽可能与t相等，从而达到学习的目的.

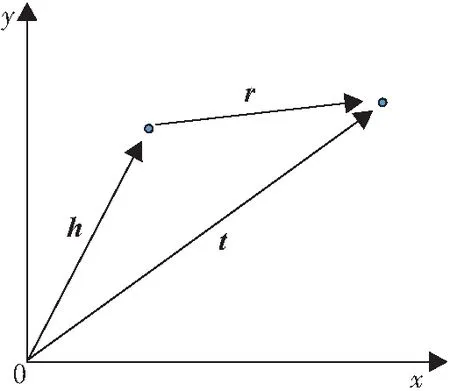
图1 TransE模型核心思想图

基于TransE模型的核心思想，BORDES等[21]的TransE实验中为三元组定义了一个得分函数，即通过头实体h和关系r之和与尾实体t的差的L1或L2距离来衡量其合理性，TransE的得分函数为：

fr(h,t)=‖h+r-t‖L1/L2,

(1)

其中，h是头实体，r是关系，t是尾实体，L1、L2分别为第一、第二范式. 对于一个正确的三元组，期望其得分越小越好；而对于一个错误的三元组，则期望其得分越高越好. TransE模型得分函数值的大小可以帮助训练模型区分正负样本. 由此，可以得到基于margin的合页损失函数为：

(2)

其中，[x]+表示x大于0时取原值，x小于0时取0；γ表示用以区分正负三元组的超参数margin，本文取γ=1；S表示正例三元组的集合，S′表示被随机替换了头实体或尾实体的负例三元组的集合.

TransE模型训练的伪代码[21]如下:

Input: Training setS={(sub,rel,obj)},marginγ,learning rate

r←/‖‖ for each

Loop

e←e/‖e‖ for each entity ent

Sbatch←sample(S,b) ∥sample minibatch of sizeb

Tbatch←∅ ∥initialize set of pairs

(sub′,rel,obj′)←sample(S′(sub,rel,obj)) ∥sample negative triplet

Tbatch←Tbatch∪{((sub,rel,obj),(sub′,rel,obj′))}

end for

End loop

1.2 TransH模型

TransE模型具有参数少、计算复杂度低的优点，但在处理非一对一关系时存在缺陷，因此，WANG等[22]对TransE模型进行了改进，提出了TransH模型. 为了解决模型在处理不同关系时需要赋予不同的关系向量这一问题，TransH模型为每个关系r定义了一个超平面，并用关系r在该平面上的平移向量r′和法向量w来进行表示. 其核心思想为：给定一个真实三元组(h，r，t)，头实体向量h和尾实体向量t沿法向量w投影到超平面上，并在超平面上进行翻译(图2). 其得分函数为：

(3)

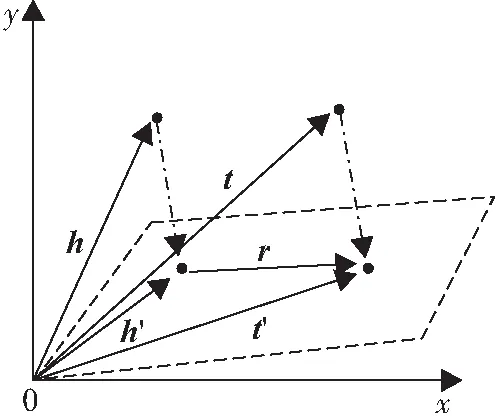
图2 TransH模型核心思想图

在实际情况中，关系对应的头尾实体是不平衡，即存在非一对一关系，采用随机负采样的方法来替换头尾实体并不合理，因此，TransH采用伯努利负采样的方法来构造负例三元组：如果关系是一对多的，则使用更大的概率来替换头实体，反之则使用更大的概率来替换尾实体. 具体步骤如下：

第一步，需要在所有三元组中统计每个头实体的平均尾实体数(记为Nt)、每个尾实体的平均头实体数(记为Nh)，定义一个带抽样参数的伯努利分布为：

(4)

第二步，在训练过程中,以P(X=1)的概率来替换头实体，构造负例三元组；以P(X=0)的概率来替换尾实体，构造负例三元组.

2 实验与讨论

2.1 实验数据

研究区域选择广州市天河区，共计118 807个标准地址数据，数据包括地址名称和地址经纬度. 根据2009年国家标准化管理委员会发布的数字城市地理信息公共平台地名/地址编码规则[23]，结合实际地址命名情况，标准地址名称大致分为5级地址：行政区域地名、街巷名、小区名、门(楼)址和标志物名[23]. 如“广东省广州市中山大道华南师范大学”的层级关系可以划分为“省-市-街道-兴趣点”(表1). 本研究以此为依据对标准地址名称进行拆分，选取兴趣点名称作为地址实体的名称，地址实体的各级街道、街路巷和用地类型作为实体之间的关系名称.

表1 地址层级关系示例Table 1 The instances of address hierarchy

本文使用RDF的数据描述方式，即将实体与关系表示为RDF数据三元组形式(头实体，关系，尾实体)或记为(h，r，t),将地址三元组表示为(地址实体名称，空间关系/语义关系，层级实体名称)，地址的层级划分为4级：居村委、街路巷、用地类型和信息点. 在设定邻近距离阈值时，如果阈值设定过大，会导致产生的邻近关系过多，影响训练效率；如果阈值设定过小，则产生的邻近关系数量太少，无法准确描述实际情况. 经过多次实验分析，选取50 m为邻近距离阈值，并根据每个信息点的经纬度来划分信息点的邻近关系，最终生成了1 420 769条三元组(表2)，根据空间地址三元组构建地址知识图谱，图谱示例见图3.

表2 数据规模Table 2 The data scale 条

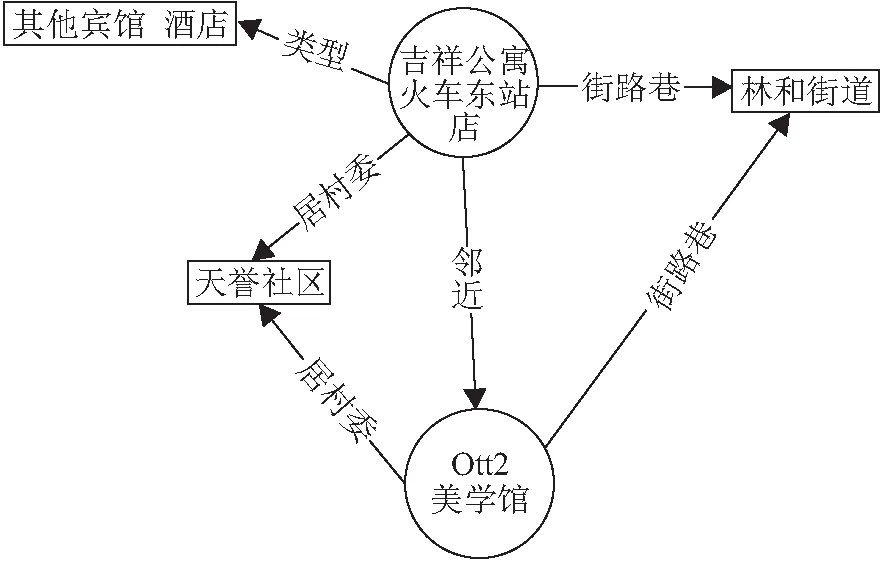
图3 地址知识图谱展示

2.2 模型对比实验设计

将三元组分别按照TransE和TransH要求的数据格式输入，模型训练的参数设置如下：随机梯度下降学习率为0.01、margin为1、batch为5 000、维度k为128、迭代次数为2 000；经过训练后，两模型的得分值loss均从20下降至0.1以下，最终得到地址实体的向量化表示. 模型训练流程如图4所示，以向量化的实体为基础进行元组分类和距离评估.

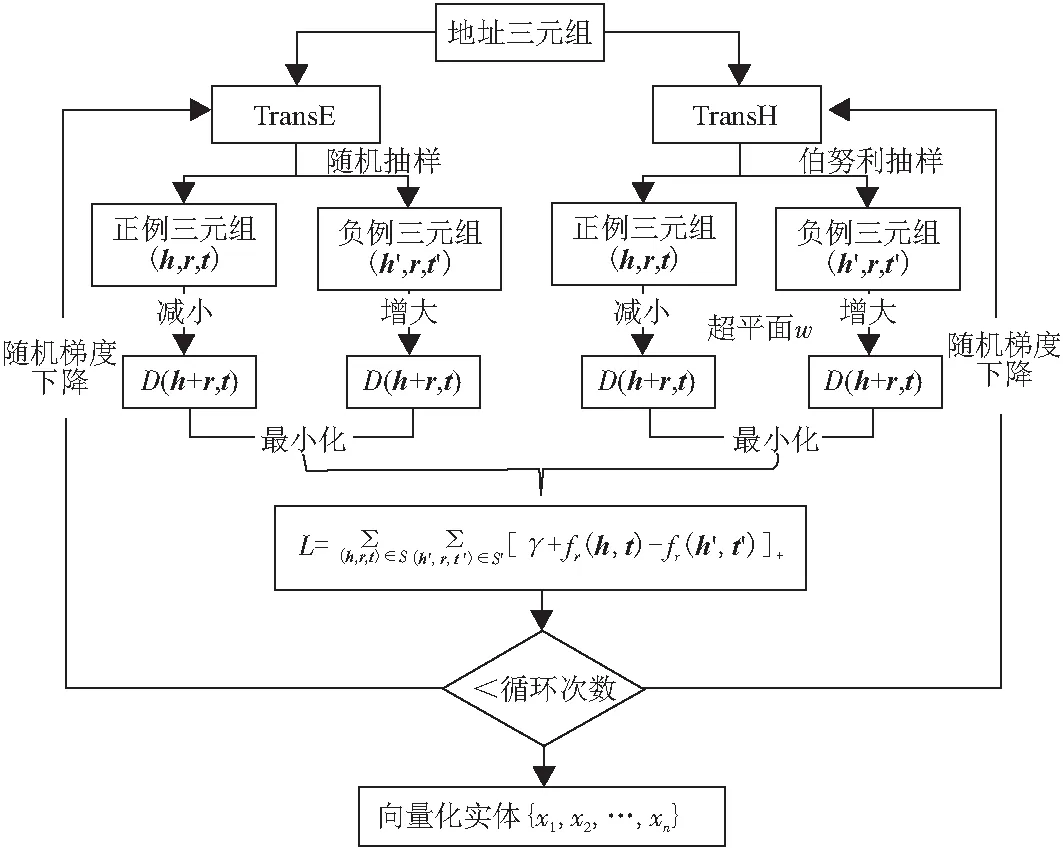
图4 TransE模型和TransH模型的训练流程图

2.3 表示学习模型比较实验

本研究的目标是从地址知识库中抽取出空间地址三元组数据集，分别使用TransE模型和TransH模型进行训练，得到实体的向量化表示；根据实体间的向量距离来比较2个模型在空间地址三元组数据集中的优劣；通过选取测试样本分别计算实体空间距离、实体语义相似度和实体间的向量距离，通过对比分析验证本实验所解决的空间关系和语义关系不一致问题.

2.3.1 实现TransE模型和TransH模型的算法 基于TransE模型，使用开源库TensorFlow进行模型训练，其实现过程中最关键的步骤是计算图的设计和负例三元组的构建：

(1)TransE模型实验及部分代码实现. 本实验先将序列化的实体、关系和训练样本进行内存读取；训练时，对每个epoch、每个batch、每个样本计算正例三元组的loss和负例三元组的loss，通过随机梯度下降更新模型嵌入，生成模型文件. TransE模型在Tensorflow的计算图python代码如下：

def build_graph_TransE(self):

self.headEntityVector=tf.placeholder(tf.int32,[None],name=“headEntityVector”)

self.tailEntityVector=tf.placeholder(tf.int32,[None],name=“tailEntityVector”)

self.relationVector=tf.placeholder(tf.int32,[None],name=“relationVector”)

self.ones=tf.placeholder(tf.float32,[None],name=“one”)

self.headEntityVectorWithCorruptedTriplet=tf.placeholder(tf.int32,[None],name=“headEntityVectorWithCorruptedTri-plet”)

self.tailEntityVectorWithCorruptedTriplet=tf.placeholder(tf.int32,[None],name=“tailEntityVectorWithCorruptedTri-plet”)

headEntityVector_embedding=tf.nn.embedding_lookup(self.embedding,self.headEntityVector)

tailEntityVector_embedding=tf.nn.embedding_lookup(self.embedding,self.tailEntityVector)

relationVector_embedding=tf.nn.embedding_lokup(self.embedding,self.relationVector)

headEntityVectorWithCorruptedTriplet_embedding=tf.nn.embedding_lokup(self.embedding,self.headEntityVectorWithCorruptedTriplet)

tailEntityVectorWithCorruptedTriplet_embedding=tf.nn.embedding_lokup(self.embedding,self.tailEntityVectorWithCorrup-tedTriplet)

headtailrel=tf.subtract(tf.add(headEntityVector_embedding,relationVector_embedding),tailEntityVector_embedding)

headtail_corrupted=tf.subtract(tf.add(headEntityVectorWithCorruptedTriplet_embedding,relationVector_embedding),tailEntityVectorWithCorruptedTriplet_embedding)

headtailrel_square_sum=tf.reduce_sum(tf.pow(headtailrel,2),1)

headtailrel_corrupted_square_sum=tf.reduce_sum(tf.pow(headtailrel_corrupted,2),1)

headtailrel_loss=tf.subtract(headtailrel_square_sum,headtailrel_corrupted_square_sum)

loss=tf.add(headtailrel_loss,self.ones)

loss_max=tf.nn.relu(loss)

loss_v=tf.reduce_mean(loss_max)

optimizer=tf.train.AdamOptimizer(0.01)

train_op=optimizer.minimize(loss_v)

returnatrain_op,loss_v,headEntityVector_embedding,tail-EntityVector_embedding,headEntityVectorWithCorruptedTriplet_embedding,tailEntityVectorWithCorruptedTriplet_embedding,relationVector_embedding

(2)TransH模型实验及代码实现. TransE模型和TransH模型的算法计算流程相似，不同之处在于：模型训练过程中，需要设计一个平面嵌入向量w，计算不同样本的正负例三元组时，要用投影在平面上的头尾实体向量来计算loss，且采用伯努利负采样的方法构造负例三元组. TransH模型在Tensorflow的计算图 python代码如下：

def build_graph_TransE(self):

_w=tf.get_variable(name=“w”,shape=[128,1],dtype=tf.float32)

w=tf.nn.l2_normalize(_w,name=“L2_normalize_w”)

self.headEntityVector=tf.placeholder(tf.int32,[None],name=“headEntityVector”)

self.tailEntityVector=tf.placeholder(tf.int32,[None],name=“tailEntityVector”)

self.relationVector=tf.placeholder(tf.int32,[None],name=“relationVector”)

self.ones=tf.placeholder(tf.float32,[None],name=“one”)

self.headEntityVectorWithCorruptedTriplet=tf.placeholder(tf.int32,[None],name=“headEntityVectorWithCorrupted-Triplet”)

self.tailEntityVectorWithCorruptedTriplet=tf.placeholder(tf.int32,[None],name=“tailEntityVectorWithCorruptedTrip-let”)

headEntityVector_embedding=tf.nn.embedding_lookup(self.embedding,self.headEntityVector)

tailEntityVector_embedding=tf.nn.embedding_lookup(self.embedding,self.tailEntityVector)

relationVector_embedding=tf.nn.embedding_lokup(self.embedding,self.relationVector)

headEntityVectorWithCorruptedTriplet_embedding=tf.nn.embedding_lokup(self.embedding,self.headEntityVectorWithCorruptedTriplet)

tailEntityVectorWithCorruptedTriplet_embedding=tf.nn.embedding_lokup(self.embedding,self.tailEntityVectorWithCorruptedTriplet)

headEntityVector_embedding_w=tf.matmul(tf.matmul(headEntityVector_embedding,w),tf.transpose(w))

tailEntityVector_embedding_w=tf.matmul(tf.matmul(tail-EntityVector_embedding,w),tf.transpose(w))

headEntityVectorWithCorruptedTriplet_embedding_w=tf.matmul(tf.matmul(headEntityVectorWithCorruptedTriplet_embedding,w),tf.transpose(w))

tailEntityVectorWithCorruptedTriplet_embedding_w=tf.matmul(tf.matmul(tailEntityVectorWithCorruptedTriplet_embedding,w),tf.transpose(w))

headtailrel=tf.subtract(tf.add(headEntityVector_embedding-headEntityVector_embedding_w,relationVector_embedding),tailEntityVector_embedding-tailEntityVector_embedding_w)

headtail_corrupted=tf.subtract(tf.add(headEntityVectorWithCorruptedTriplet_embedding-headEntityVectorWithCorrup-tedTriplet_embedding_w,relationVector_embedding),tailEntity-VectorWithCorruptedTriplet_embedding-,tailEntityVectorWithCorruptedTriplet_embedding_w)

headtailrel_square_sum=tf.reduce_sum(tf.pow(headtailrel,2),1)

headtailrel_corrupted_square_sum=tf.reduce_sum(tf.pow(headtailrel_corrupted,2),1)

headtailrel_loss=tf.subtract(headtailrel_square_sum,headtailrel_corrupted_square_sum)

loss=tf.add(headtailrel_loss,self.ones)

loss_max=tf.nn.relu(loss)

loss_v=tf.reduce_mean(loss_max)

optimizer=tf.train.AdamOptimizer(0.01)

train_op=optimizer.minimize(loss_v)

returnatrain_op,loss_v,headEntityVector_embedding,tail-EntityVector_embedding,headEntityVectorWithCorruptedTriplet_embedding,tailEntityVectorWithCorruptedTriplet_embedding,relationVector_embedding

(3)TransE模型的负例三元组的构建python代码如下：

def getCorruptedTriplet(self,triplet):

i=uniform(-1,1)

if i<0:

while True:

entityTemp=sample(self.entityList,1)[0]

if(entityTemp,triplet[1],triplet[2]) not in self.filter: break

corruptedTriplet=(entityTemp,triplet[1],triplet[2])

else:

while True:

entityTemp=sample(self.entityList,1)[0]

if(triplet[0],entityTemp,triple[2]) not in self.filter:

break

corruptedTriplet=(triplet[0],entityTemp,triplet[2])

return corruptedTriplet

(4)TransH模型的负例三元组的构建python代码如下(本实验中，每个头实体的平均尾实体数为13，每个尾实体的平均头实体数为18)：

def getCorruptedTriplet(self,triplet):

i=uniform(0,31)

if i<13:

while True:

entityTemp=sample(self.entityList,1)[0]

if(entityTemp,triplet[1],triplet[2]) not in self.filter:

break

corruptedTriplet=(entityTemp,triplet[1],triplet[2])

else:

while True:

entityTemp=sample(self.entityList,1)[0]

if(triplet[0],entityTemp,triple[2]) not in self.filter:

break

corruptedTriplet=(triplet[0],entityTemp,triplet[2])

return corruptedTriplet

2.3.2 模型评估 由于本实验选择的数据集为空间地址三元组，无法通过已有知识进行推理预测，例如A地址与B地址是邻近关系，B地址与C地址是邻近关系，无法证明A地址与C地址也是邻近关系. 因此，本实验不选择链接预测和文本关系事实抽取作为评估方法. 考虑到地址实体间除了包含语义关系，还包含有空间距离关系，因此，本实验选择元组分类和向量距离评估作为模型评估方法.

2.4 元组分类

元组分类是指判断一个给定的三元组(h，r，t)是否属于正确的三元组，实质上是一个二分类任务. 例如：给定一个三元组(吉祥公寓火车东站店，Near，Otto2美学馆)，计算头实体向量加关系向量与尾实体向量之间的距离(h+r-t)，根据h+r-t是否小于阈值来判断三元组是否正确(通过验证集来确定阈值大小).

通过随机选取1 000条三元组来构造测试数据集，得到TransE模型和TransH模型的分类准确率分别为71.7%和88.5%. 从分类准确率的结果来看，TransH模型确实优于TransE模型，其原因在于：在中文地址数据集中非一对一关系较多，因此，引入了超平面投影的TransH模型在中文地址数据集中的三元组分类任务表现较为优秀，表明对复杂关系的建模在中文地址数据的向量离散化任务中是有优化作用的.

2.5 距离评估

距离评估是指在不同模型中，分别计算正负例三元组中实体间的向量距离(h+r-t)，根据翻译模型训练的机制(即缩小正例三元组中h+r与t之间的距离，增大负例三元组中h+r与t之间的距离)，以此来评估模型的优劣.

通过1∶1关系构造正负三元组验证集，分别计算其在TransE模型和TransH模型中的向量距离，由结果(表3)可知：TransH模型在正例三元组中实体间的向量距离(0.525)优于TransE模型的(0.531)，然而TransE模型在负例三元组中实体间的向量距离(1.388)优于TransH模型的(1.379)；TransE模型的正负例距离差(0.857)略优于TransH模型的(0.854)，表明TransE、TransH模型对同一三元组的实体距离的训练结果是相似的.

表3 三元组中实体间的向量距离Table 3 The vector distance between entities of a triple

然而，选取相同的3个地址实体进行对比分析，由结果(图5，图6)可知：

(1)无论是TransE模型还是TransH模型，存在关系的两实体的向量距离确实比不存在关系的两实体的向量距离要小得多. 例如，在TransE模型的训练结果中，吉祥公寓火车东站店与Otto2美学馆的向量距离(0.545)远小于吉祥公寓火车东站店与汇悦台东门幼儿园的向量距离(1.414)；在TransH模型的训练结果中，吉祥公寓火车东站店与Otto2美学馆的向量距离(0.533)同样远小于吉祥公寓火车东站店与汇悦台东门幼儿园的向量距离(1.335).

(2)在TransH模型中，存在邻近关系的实体间的向量距离要小于不存在邻近关系的实体间的向量距离. 例如，不存在邻近关系的吉祥公寓火车东站店与汇悦台东门幼儿园的向量距离(1.335)大于不存在任何关系的宾馆与幼儿园的向量距离(1.235)；而存在邻近关系的吉祥公寓火车东站店与Otto2美学馆的向量距离(0.533)小于存在街路巷关系的Otto2美学馆与天誉社区的向量距离(0.552).

(3)TransE模型中，通过向量距离表现实体语义关系的情况并不明显. 例如，存在邻近关系的吉祥公寓火车东站店与Otto2美学馆的向量距离(0.545)小于存在街路巷关系的吉祥公寓火车东站店与林和街道的向量距离(0.601)，却大于存在居村委关系的Otto2美学馆与天誉社区的向量距离(0.513).

从表2可以发现地址三元组数据集中邻近关系的数量远远大于其他几种语义关系，空间关系相较于语义关系的复杂程度更高，由此可以推测：TransH模型相较于TransE模型，更加注重于对复杂关系的建模.

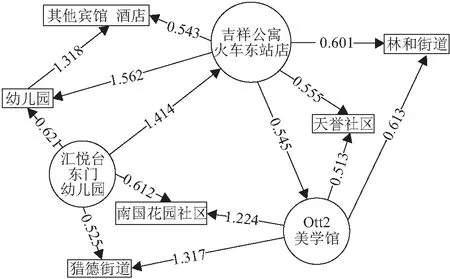
图5 TransE模型中实体间的向量距离

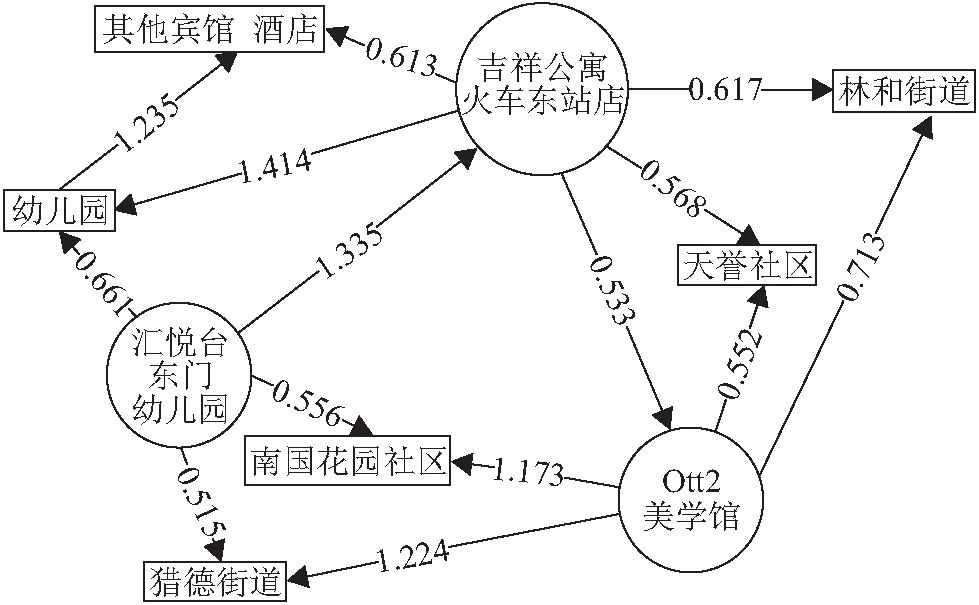
图6 TransH模型中实体间的向量距离

2.6 实验结果分析

由上述元组分类和向量距离评估的结果可知：TransH模型优于TransE模型. 因此，选择TransH模型的训练结果作为评判本研究所要解决的传统地址实体语义和空间相似性不一致问题的量化标准.

选取6个地理实体，分别为：太平洋电脑城、百脑汇电脑城、怡东电脑城、火炬大厦、壬丰大厦、摩登百货，后文依次用A、B、C、D、E、F替代. 通过两点经纬度坐标计算各地理实体间的直线距离：L(AB)=0.1 km，L(AC)=0.2 km，L(DE)=0.5 km，L(DF)=0.2 km；通过TransH模型训练得到的实体向量分别得到各地理实体间的向量距离：V(AB)=1.131，V(AC)=0.551，V(DE)=1.312，V(DF)=0.571. 针对地理实体语义相似性的计算，考虑到地理实体为短文本，故选用较为简单高效的余弦相似度计算方法，得到各地理实体间的语义距离：S(AB)=0.67，S(AC)=0.58，S(DE)=0.5，S(DF)=0，由此可以看出：(1)V(AC)S(DF)，实体D、E、F都属于岗顶街道，但是L(DF)

3 结论

传统研究中仅使用地址语义关系来计算两地址实体的相似程度，存在距离相近而语义不相似或语义相似而距离不相近的问题，针对这个问题，本文提出使用知识表示学习的方法对地址实体进行向量化表示. 通过对比TransE模型和TransH模型的训练结果，验证了在地址实体的表示学习任务中，TransH模型的表示学习效果明显优于TransE模型. 空间关系和语义关系的结合，能够很好地解决地址实体之间可能存在的语义和空间不一致的问题，更好地通过向量间距离来表示地址实体之间的紧密程度. 同时，中文数据集在知识表示学习中的使用，能够丰富翻译模型在中文数据集的知识表示研究，也能帮助我们更好地针对中文文本进行文本语义研究，方便将研究进行成果转化.