短程相互作用对准粒子相对论动力学的影响
李 志,胡 玥,郭政鑫,陈李梅,黄育蕾
(华南师范大学物理与电信工程学院, 广州 510006)
量子多体问题一直是物理学领域的一个重要研究方向. 长期以来关于多体相互作用在Dirac色散关系中的影响研究,无论是理论研究还是实验研究均受到广泛关注[1-5]. 在一维情况下,由于存在短程相互作用,可使费米子两两合成玻色子. 从而产生玻色子的集体激发,最终导致费米液体转变为Luttinger液体[1-2]. 最近,在二维情况(例如石墨烯[3]和拓扑绝缘体[4])下,Dirac准粒子的研究也引起了广泛关注. 一方面,长程库仑相互作用[5]对重整化费米速度有明显影响,但不会导致任何相变[6];另一方面,足够强的短程库仑相互作用可引起绝缘行为[3,7-12].
近些年来,Dirac点的融合问题引起了人们的极大兴趣. 此类系统中二维Dirac费米子以及相关的拓扑相变问题相继被研究[13-17]. Dirac点的融合导致了奇异的色散关系:在一个方向上表现为线性,而在其他正交方向上表现为抛物线性. 融合标志着一个由半金属相到带绝缘相的拓扑量子Lifshitz相变[13-16]. 最近,瑞士ETH冷原子实验室在一个几何可调光晶格系统中装载超冷原子,在实验上实现了对Dirac点的操控,并最终实现了融合相变[17]. 这种光晶格中超冷原子体系为量子模拟提供了一个有效的工具,使凝聚态系统和多体物理系统的特性研究能够通过完全可控的方式进行[4]. 随后,Hubbard模型的超流-Mott绝缘相变等相互作用诱导的现象,很快在冷原子晶格中被逐一实现[18]. 此外,在光学晶格上加载超冷中性原子,可以得到石墨烯的相似物. 这使许多著名相对论物理现象的观测成为可能. 例如Klein遂穿[19]、ZB效应[20-22]等. 随着冷原子量子模拟器件的日益成熟,在冷原子系统中,对于特殊色散关系与相互作用并存的准粒子动力学特性的研究逐步升温[23].
本文通过调节相互作用诱发系统Dirac点的融合,研究此过程中系统的准粒子动力学特性. 为了避免ZB效应以及系统维度对融合的影响,考虑最简单的一维SSH模型[24-25],通过引入短程相互作用,定性讨论系统的相变与准粒子动力学行为. 此外,通过数值研究方法直接模拟,给出融合过程中不同时间Dirac准粒子的演化情况,得到此过程中波包中心随时间变化的解析表达式.
1 模型构建与冷原子模拟
1.1 模型构建
聚乙炔原子链SSH模型是最典型的一维拓扑材料[24-25],其晶格排布和电子跳跃情况如图1A所示. 在不考虑短程相互作用的情况下,系统的能带结构与拓扑Zak相如图1B、C所示.
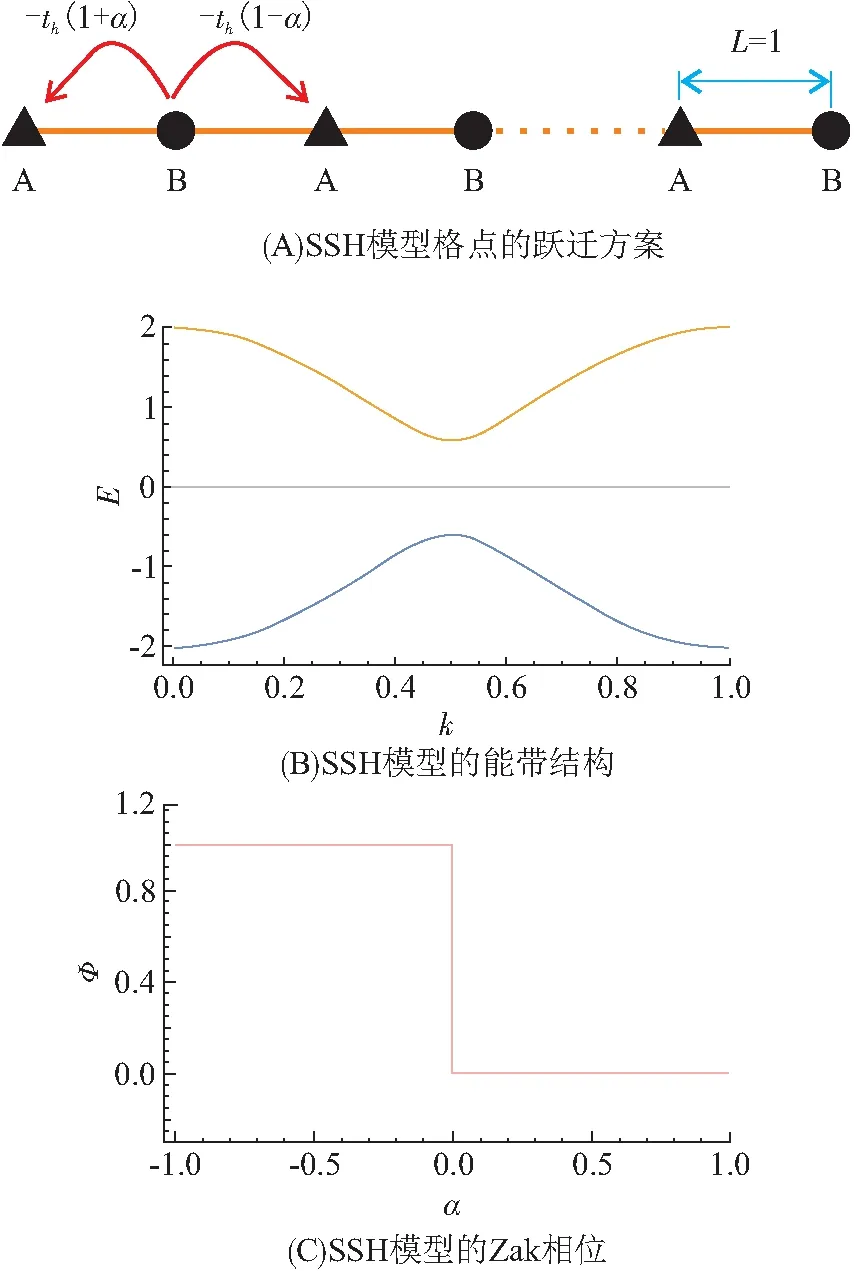
图1 SSH模型格点的跃迁方案、能带结构及Zak相位
由于Peierls的不稳定性(图1C)导致聚乙炔原子链会形成AB子格结构(即SSH模型). 通过调节参数α,系统发生拓朴相变,可通过计算系统的Zak相来表征系统的拓扑特性(图1C). SSH模型中的低能有效哈密顿具有线性色散特性,相应的准粒子动力学行为可用Dirac方程描述[25]. 本文从具有短程相互作用的SSH模型出发,为简单起见,仅考虑固定的短程相互作用(U). 此时,系统中一维Dirac准粒子的动力学特性可用1+1维Dirac方程[16]描述:
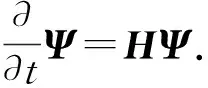
(1)
哈密顿量
(2)
其中,m*为准粒子有效质量,Δ是能带结构参量,σx是泡利矩阵,px是x方向的动量算符,Δ取决于晶格内部或晶格之间的粒子跃迁特性.系统的相对论能量-动量关系可写为
(3)
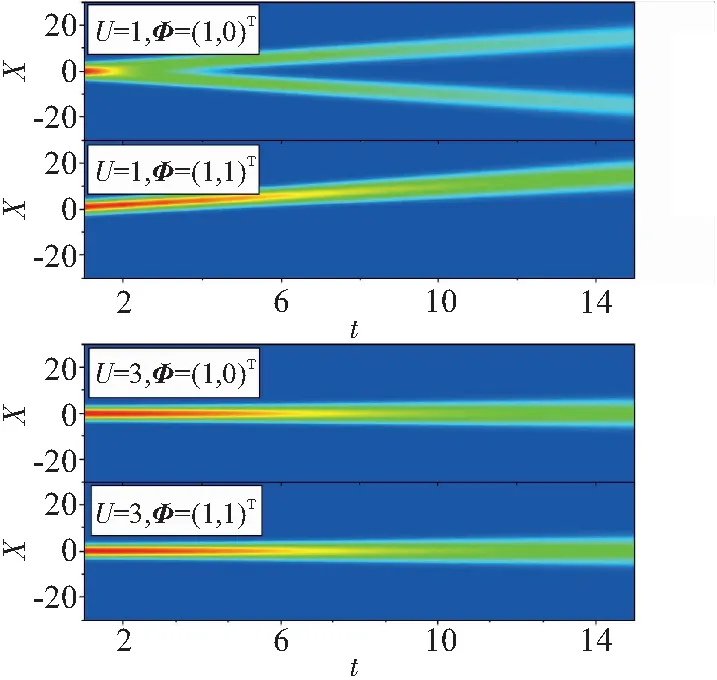
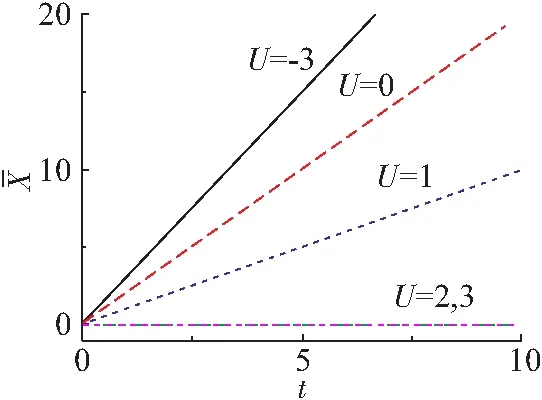
当Δ取固定值时,Dirac点融合的过程仅由短程相互作用参数U来决定. 通过改变U,可以控制Dirac点相互靠近并最终融合. 如图2所示,当Δ>U时,色散关系显示出2个Dirac点,在这2个Dirac点中间存在一个马鞍形状的间隙;当Δ=U时,2个狄拉克点恰好融合在一起,且在融合过程中,随着|U-Δ|的增大,线性色散关系的斜率增大. 由于色散关系的斜率对应于波包的运动速度,所以这将导致波包定向移动的速度随着|U-Δ|的减小而减小,并最终在融合点处趋于零. 在融合之后,进一步增大相互作用使|U-Δ|继续增大,此时Δ 图2 相对论和非相对论区域的能带结构 对冷原子系统中的前述现象进行实验模拟:(1)需要将Rb87原子装载到磁光阱中来实现超冷原子;(2)用固定波长的激光器实现一维光晶格,利用拉曼光打开辅助跃迁窗口,实现SSH模型晶格,并在光学系统中加入可调Fechbach共振组件;(3)将原本囚禁在谐振势中的超冷Rb87原子装载到SSH晶格中,关闭谐振势,打开Fechbach共振系统,使得系统拥有一个固定的短程相互作用,让Rb87原子在此SSH晶格中作时间飞行(time-of-flight);(4)利用吸收成像技术即可探测原子云的密度分布. 整个过程所采用的操作手段均为目前比较成熟且广泛使用的冷原子实验技术. 上述从相对论到非相对论动力学过渡的现象,可以较容易地在冷原子实验平台中实现. 通过固定参量,在相互作用U不同时,直接求解1+1维Dirac方程. 计算时取高斯型波包为初态波函数, (4) 其中,Φ=(c1,c2)T为单位矢量,T为矩阵转置符号,d为波包宽度,kx是x方向的波矢. 这个两组分的波函数被称为Dirac旋量,反映了低维空间中的正、负能量. 因此,准粒子在动量空间对应的波函数为 (5) 图3 相对论和非相对论区域的准粒子波包演化 在海森堡绘景中,含时位置算符可以表示为 r(t)=eiHt/ћr(0)e-iHt/ћ. (6) 将哈密顿H代入式(6)可得x(t)的表达式 (7) 其中, 显然x(t)是一个2×2的矩阵. 前两项是自由Dirac粒子的经典动力学项,而第三、四项是导致ZB振荡出现的原因. 这里为了避免ZB振荡的影响,获得一个融合前后清晰直观的波包动力学图像,本文考虑融合前色散关系无能隙的情况,这就导致了表达式中与ZB振荡相关的两项系数均为0. 在下面的理论分析中,取相同的高斯型初态波包. 若初始波包取Φ=(1,0)T,则相当于取出 (8) (1)对Δ>U(相对论范围)的情况进行讨论. 此时,若保持准粒子波包位于Dirac点处,则需满足 图4 能带参数Δ=2情况下Dirac点融合过程中系统的世界线 基于超冷原子SSH晶格模型,研究了短程相互作用对系统能带和动力学行为的影响. 通过Fechbach共振可以比较方便地操控短程相互作用(从吸引到排斥),进而操控系统能带中Dirac点的融合相变. 此外,本文以SSH模型为例,讨论了一维系统中准粒子动力学处于相对论区域与非相对论区域的区别. 初态旋量取σx本征态时,相对论与非相对论粒子质心均保持在初始中心,但波包的演化具有明显的区别. 从数值模拟的准粒子演化情况可以看出,相对论范围的准粒子会发生劈裂,而非相对论范围的准粒子始终缓慢扩散. 初态旋量选取σz本征态时,相对论准粒子具有一个初速度,而非相对论准粒子依然保持缓慢扩散的特性. 不难验证,对于二维、三维情况的系统也具有类似的特性. 超冷原子晶格体是目前比较成熟的量子模拟器件之一. 因此,研究结果可以为此系统实验观测相对论动力学特性提供新的思路,即从动力学的角度,通过观测波包的密度分布情况判断系统的能带结构. 冷原子系统的高可操控性以及高度纯净等优势,上述有趣的动力学现象有望在冷原子系统中被观测到.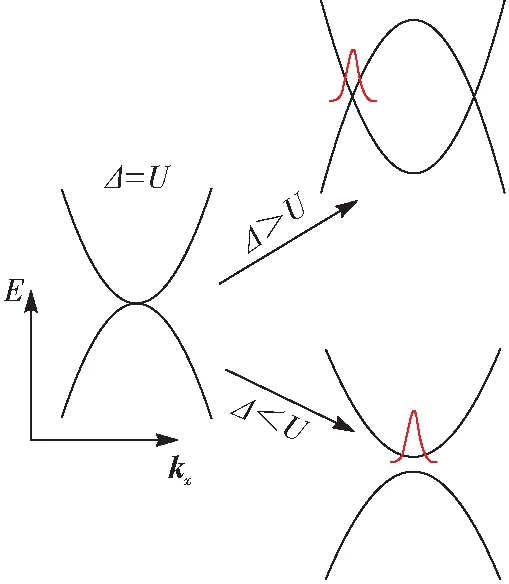
1.2 冷原子模拟
2 计算结果分析

3 世界线的解析分析
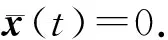
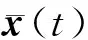
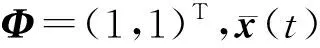
4 结论

