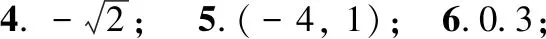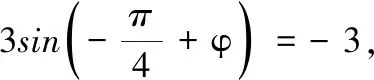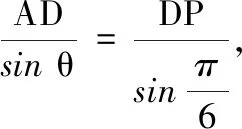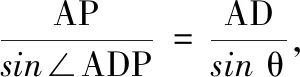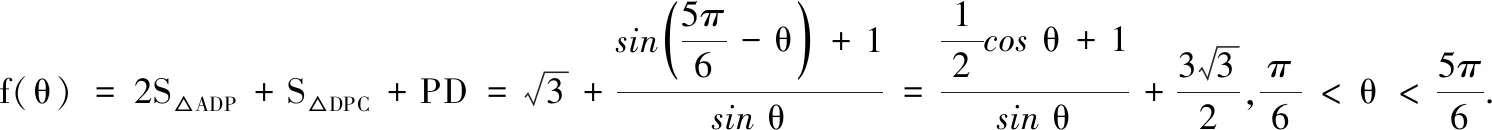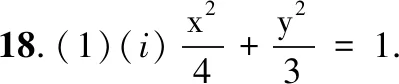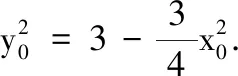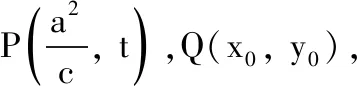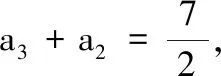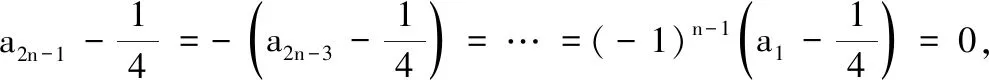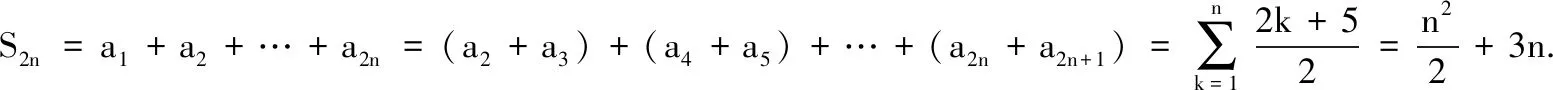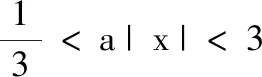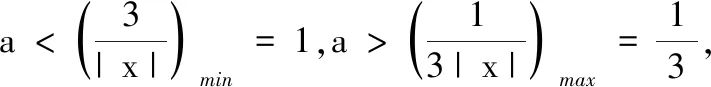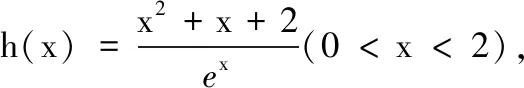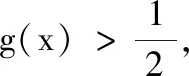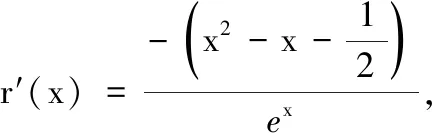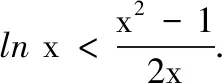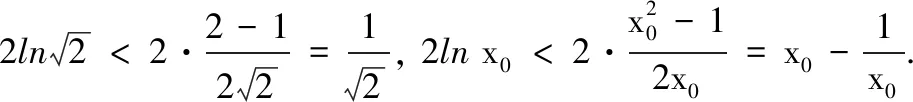高三数学综合测试

一、填空题(本大题共14小题，每小题5分，计70分)

1.已知集合A={-1, 0, 3, 5},B={x|x-2>0},则A∩B=______.

2.已知(1+3i)(a+bi)=10 i,其中i为虚数单位,a，b∈R,则ab的值为______.

3.已知一组数据82,91,89,88,90,则这组数据的方差为______.

4.根据如图所示的伪代码,已知输出值y为3,则输入值x为______.

5.y=lg(4-3x-x2)的定义域为______.

6.袋中有若干只红、黄、蓝三种颜色的球,这些球除颜色外完全相同.现从中随机摸出1只球,若摸出的球不是红球的概率为0.8,不是黄球的概率为0.5,则摸出的球为蓝球的概率为______.

7.在∆ABC中,若sinA∶sinB∶sinC=4∶5∶6,则cosC的值为______.

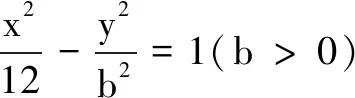
9.已知{an}是等比数列,Sn是其前n项和.若a3=2,S12=4S6,则a9的值为______.

11.已知实数a，b，c成等比数列,a+6、b+2、c+1成等差数列,则b的最大值为______.

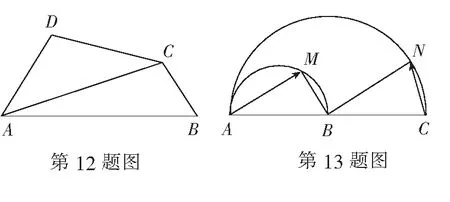
12.如图,在平面四边形ABCD中,边AB=4,AD=2,∠DAB=60°,且AC=3BC,则边CD长的最小值为______.

二、解答题(本大题共6小题,计90分.解答应写出文字说明、证明过程或演算步骤)

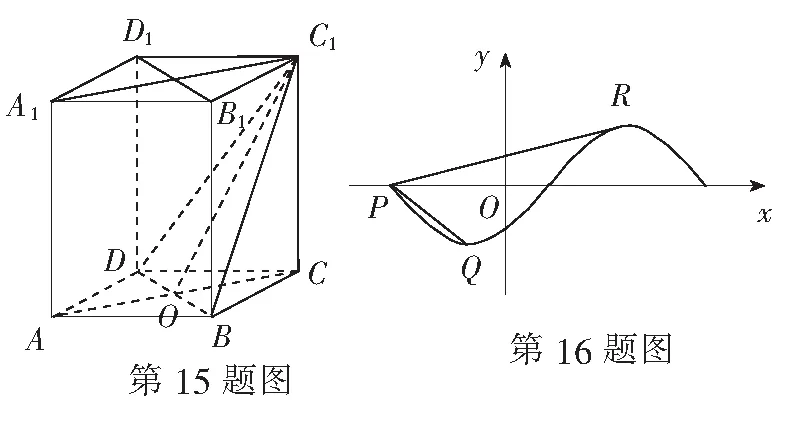
15.(本小题满分14分)如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为平行四边形,C1B=C1D.求证:

(1)B1D1∥平面C1BD;

(2)平面C1BD⊥平面AA1C1C.

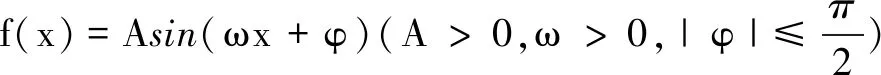
(1)求函数f(x)的解析式;

(2)记∠RPO=α,∠QPO=β(α，β均为锐角)，求tan(2α+β)的值.

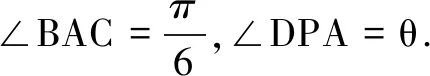
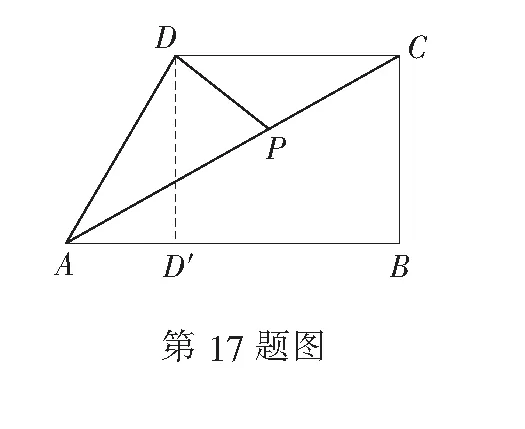
(1)用θ表示直道DP的长度;

(2)计划在∆ADP区域内种植观赏植物,在∆CDP区域内种植经济作物.已知种植观赏植物的成本为每平方百米2万元,种植经济作物的成本为每平方百米1万元,新建道路DP的成本为每百米1万元,求以上三项费用总和的最小值.

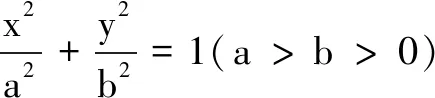
(i) 求椭圆的方程；

(ii) 若直线OQ，PQ的斜率分别为k1，k2,求k1k2的值;

(2)若在x轴上方存在P，Q两点,使O，F，P，Q四点共圆,求椭圆离心率的取值范围.

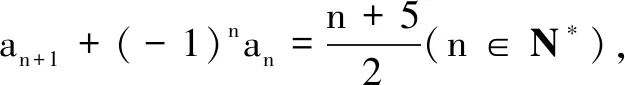
(1)求a1+a3的值；

(2)若a1+a5=2a3；

(i)求证：数列{a2n}为等差数列；

(ii)求满足S2p=4S2m(p,m∈N*)的所有数对(p，m).

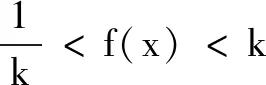
(1)设f(x)=a|x|，定义域D=[-3,-1]∪[1,3].若f(x)是D(3)型函数,求实数a的取值范围;

(2)设函数g(x)=ex-x2-x,定义域D=(0，2)，判断g(x)是否为D(2)型函数，并给出证明.(参考数据：7

参考答案

一、填空题

1.{3, 5};2.3;3.10;

二、解答题

15.(1)因为BB1∥DD1,且BB1=DD1,所以四边形BDD1B1为平行四边形,从而B1D1∥BD.

又BD⊂平面C1BD,B1D1⊄平面C1BD,所以B1D1∥平面C1BD.

(2)设AC与BD交于点O,连结C1O.因为底面ABCD为平行四边形,所以O为BD的中点;又C1B=C1D,所以C1O⊥BD.

在直四棱柱ABCD-A1B1C1D1中,C1C⊥平面ABCD,又BD⊂平面ABCD,所以C1C⊥BD.又因为C1O∩C1C=C1,C1O，C1C⊂平面AA1C1C,所以BD⊥平面AA1C1C.

又BD⊂平面C1BD,所以平面C1BD⊥平面AA1C1C.

(2)结论:g(x)是D(2)型函数.

①