应用斜三角形的一条性质解题
2020-08-05 12:29陈万龙
高中数学教与学 2020年11期
陈万龙
(湖南省华容县第二中学,414215)
性质在斜三角形ABC中,恒有
tanA+tanB+tanC=tanAtanBtanC.
①
由两角和的正切公式,易证斜三角形具有的如上性质.恰当灵活应用① 式,能快速有效处理斜三角形的某些问题.
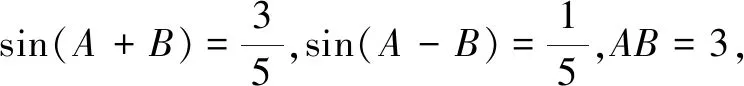
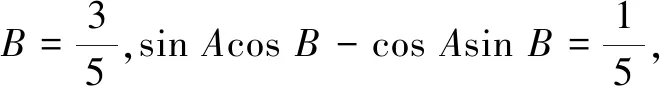
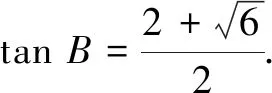
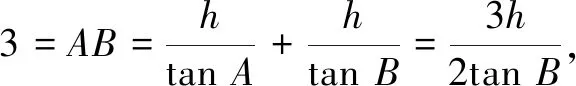
评注本题由条件及① 式通过消元直接求得tanB,再从整体上用tanB来表示AB边上的高,给问题求解提供了新思路.
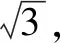
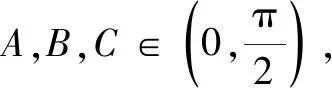
tanAtanBtanC=tan3B.
利用① 式,可得
tanAtanBtanC
=tanA+tanB+tanC
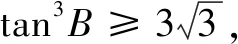
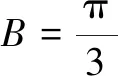
又由a2+c2-ac=4,且a=c,可得a=c=b=2.
评注本题处理的关键是求B的最小值,利用① 式与基本不等式找到了解决问题的途径;再在B取得最小值的前提下来处理三角形面积的最大值,根据余弦定理与基本不等式使问题得到了圆满的解决.
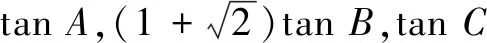
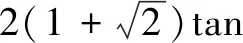
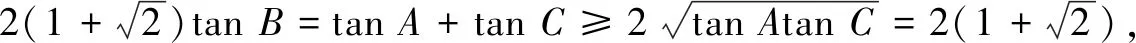
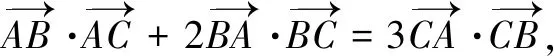
解由数量积的定义,知题设等式可化为bccosA+2accosB=3abcosC;再由正弦定理,得sinBsinCcosA+2sinAsinCcosB=3sinAsinBcosC,即
由① 式与上式消去tanA,整理可得
(tan2C-3)tan2B-2tanCtanB+2tan2C=0.
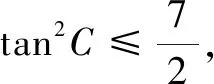
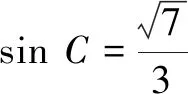
评注本题利用方程思想来处理问题,解答过程与参考答案完全不一样,可以算得上是有意义的事情.不过,此法对计算能力要求较高.
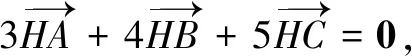
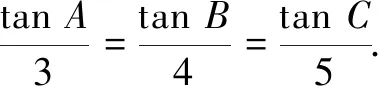
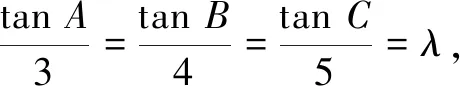
评注熟悉三角形五心的有关向量恒等式,是迅速求解本题的关键.而① 式的应用,更是加快了问题的求解过程.
练习
1.(2016年江苏高考题)在锐角∆ABC中,若sinA=2sinBsinC,则tanAtanBtanC的最小值是______.
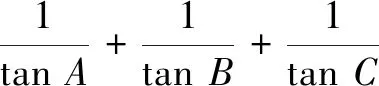
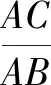
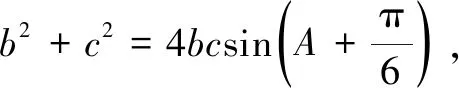
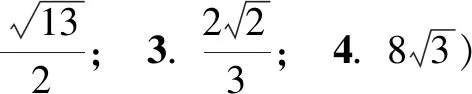
猜你喜欢
湖南水利水电(2021年6期)2022-01-18
科教新报(2021年46期)2021-01-06
中学生数理化(高中版.高二数学)(2020年11期)2020-12-14
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
河北理科教学研究(2020年1期)2020-07-24
人物画报(2020年5期)2020-01-03
中学生英语·阅读与写作(2017年6期)2017-07-18
中学生英语·中考指导版(2017年6期)2017-07-18
智富时代(2017年4期)2017-04-27
智富时代(2017年4期)2017-04-27

