妙用代数式的几何意义解题

张礼明

(广东省中山市中山纪念中学，528454)

高中数学知识中包括大量的公式和定理,很多学生因为公式繁多而害怕数学.其实,每一个数学公式和代数式都有其特殊的含义和结构,掌握好每一个代数式(或公式、不等式)的意义和结构,是学好数学的根本方法.本文举例说明利用一些常用公式的几何意义,能巧妙求解一些比较复杂的问题.

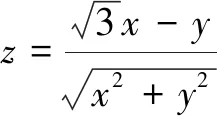
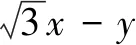
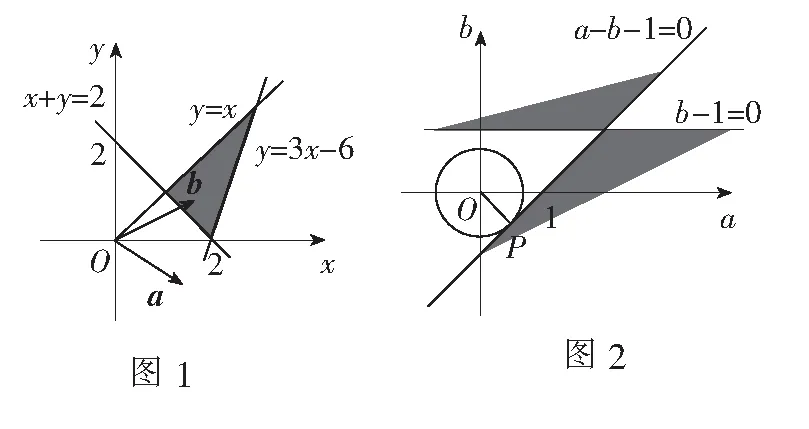
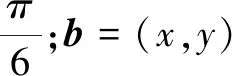
评注本题求解的难点在于识别目标函数在结构上隐含的特殊几何意义.

例2设A(1,-1),B(0,1),若直线ax+by=1与线段AB(包括端点)有公共点,则a2+b2的最小值为______.

解由直线ax+by=1与线段AB(包括端点)有公共点,得A(1,-1)，B(0,1)两点在直线ax+by=1的两侧,故(a-b-1)(0·a+b-1)≤0,即(a-b-1)(b-1)≤0.

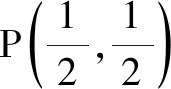
评注按常规思路,处理公共点问题是通过联立方程组求解,而该题难点在于线段AB并不是完整的直线,将直线AB的方程与ax+by=1联立方程组并不能完整刻画问题的全部特征. 转换思维角度,利用二元一次方程组对应的平面区域表示题设条件,用距离公式解读目标函数a2+b2,有效化解了问题的求解难度,增强了数学思维的灵活性.

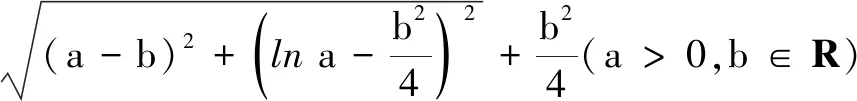
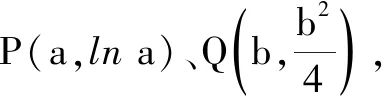
由三角形的性质,可得|PQ|+|QF|≥|PF|(P，Q，F三点共线时等号成立),故φ(a,b)≥|PF|-1.因此，只要求定点F(0,1)到动点P(a,lna)的最短距离即可.

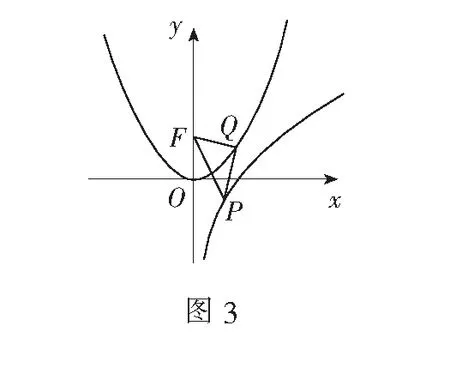
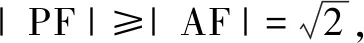
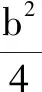
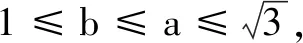
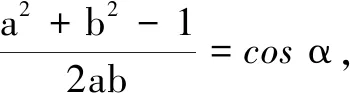
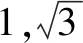
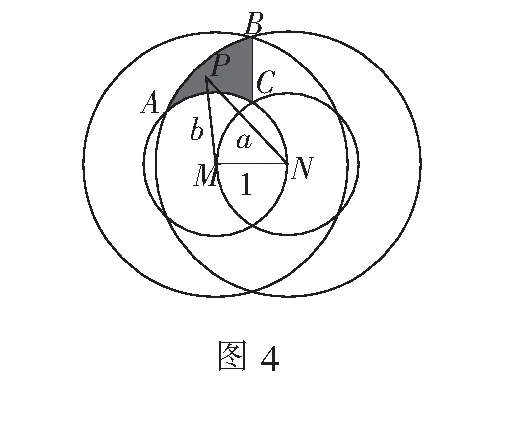
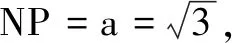
评注本题求解需充分题设条件及目标函数的几何背景,通过构造几何图形并运用图形的几何性质将多元函数问题转化为一元函数最值问题,对直观想象提出了较高要求.

其实,还有很多由公式、定理或不等式等知识组成的综合题,侧重考查同学们几何思维的灵活性,万变不离其宗的是这些问题本质意义.数学教会我们的不仅是基础知识和技能,更重要的是指引我们掌握透过现象看本质的思维方法.