导数概念与圆锥曲线的切线

黄良发

(广东省江门市第一中学,529080)

高中数学中的切线最早见于直线与圆的位置关系之中;其后,在高中数学人教A版教材选修2-1的圆锥曲线中也常常见到各类切线;而切线作为严密的数学概念却在导数一章中才给出严格的定义.导数的概念是高中数学教材中最重要、最深邃的概念之一,定义本身就体现了数学中无限逼近、以不变代变、化归转化等数学思想.

在教学中,笔者发现有不少学生常感到困惑:既然导数可以用来求曲线的切线方程,为什么在实际解题中很少见到用导数来求圆锥曲线的切线呢? 如果能,该如何求?其一般性结论是什么?作这一线教师,笔者以导数概念为出发点,探索求圆锥曲线切线方程的一般方法,供同学们参考.

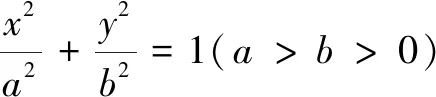
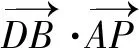
解法4利用圆的参数方程

考虑圆B的参数方程，令

通过以上几种解法,可以看出:本题看似复杂,实则简单易解.解题的关键是在于能否把问题转化为我们熟悉的问题，体现了对数学基本概念、基本思想方法和基本计算能力的要求,体现了数学逻辑推理、数学建模、数学运算等核心素养,这也是高考对我们的基本要求.

综上,结论1成立.

有了结论1,可提高解决与椭圆切线有关问题的解题速度.比如

利用导数的定义,还可以得出如下更一般性的结论.

结论2已知二次曲线Ax2+By2+Cx+Dy+E=0(A2+B2≠0),设P(x0,y0)为曲线上定点,则曲线在点P处的切线方程为

①

推论2抛物线y2=2px(p>0)上定点P(x0,y0)处的切线方程为y0y=p(x+x0).

推论3圆(x-a)2+(y-b)2=r2上定点P(x0,y0)处的切线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.