数列通项公式问题的认知结构研究*

刘晓语 陈建华

(江苏省扬州大学数学科学学院，225002)

一、引言

数列作为高中数学的重要内容是高考的重量级常客，数列问题探讨中的猜想、归纳和演绎过程也是人们对数列理性的认识过程和对美的感受过程．《普通高中数学课程标准(2017年版)》提出“了解数列的概念”，“探索并掌握等差数列和等比数列的前n项和公式”，“感受数学模型的现实意义与应用”等教学要求[1]，正是对提升学生数学运算、逻辑推理和数学建模等数学核心素养要求的具体体现．

数列的题型千变万化，特别是求解数列通项公式这部分内容，涉及类型很多，灵活度较高.求解数列通项公式问题，通常是解决综合数列问题的重点和基础.本文通过建立数学认知结构的方式,促进数列通项公式问题的解决.

二、数学认知结构的概念和意义

教育心理学认为,人的学习过程其实是将知识内化的认知过程.数学学习过程中，学生需通过主观改造，将数学知识转化为自己的数学认知结构.曹才翰教授指出:“数学认知结构就是学生头脑中的数学知识按照他自己理解的深广度，结合自己的感觉、知觉、记忆、思维、联想等认知特点，组合成的一个具有内部规律的整体结构”[2].简单来说，数学认知结构是学生建立的包含数学概念、数学命题、数学技能和数学思想方法等的整体知识结构.陈永明等认为，就数学解题而言有两个重要的数学认知结构，一个是解题模块，另一个是命题联想系统，需要帮助学生构建[3].

数学认知结构是经过学生主观改造而形成的，自然对学生学习数学有着重要的作用.在数学学习过程中，已有数学认知结构是学生学习新知识、解决新问题的有力基础．教师应该努力帮助学生构建良好的数学认知结构，以促进学生后继知识的学习和问题解决能力的提升．我们都知道等差数列(等比数列)的全部知识、全部思想都集中在等差数列(等比数列)的递推形式、通项形式、对称形式和函数形式的不同表述上;可以从两个“最原始而又不失去重要性”的两个范例去研究某些数列的通项公式．这些经验如果能形成一定的数学认知结构就能发挥更好的作用．

三、数列通项公式问题的认知结构

1. 数列通项公式问题认知结构的构建

基于对数学认知结构的理解，我们将数学解题建立的数学认知结构称为解题模块.解题模块的建立，就是将隐性的解题经验显性化、算法化，使数列通项公式问题的求解变得有规律可循，有方法可依，从而降低求解难度.通过对教材中的数列知识和大量数列题目的总结归纳，将求解数列通项公式问题分门别类地寻找所对应的可以机械化求解的方法，可以总结、绘制数列通项公式问题的解题模块(如图1所示)．

上述关于求解数列通项公式问题的解题模块，是以题干条件为切入点，根据有无递推公式进行细分的.题干条件没有递推公式的情况分为图1中三类(可能还有其他的),解决方法为观察法、公式法.这类题目一般难度不大，易求解.而有递推公式的题目，由于递推公式变化灵活，所以种类多样.但常见、常考的递推公式可总结为图1中十类.每一类递推公式都有对应的求解方法.根据上述求解数列通项公式问题的解题模块，可以简单解决大多数数列通项公式的求解问题.

2.解题模块的应用分析

下面通过几例看一下解题模块的应用.

例1(2011年山东理科卷第20题) 等比数列{an}中，a1,a2,a3分别是下表第一、二、三行中某一个数，且a1,a2,a3中的任何两个数不在下表的同一列.

第一列第二列第三列 第一行3210 第二行6414 第三行9818

(1) 求数列{an}的通项公式;(2)略．

分析根据解题模块，首先看题目条件，未给出递推公式，题干是以图表法的形式展现的，所以，用观察法找数字之间的规律.

解(1)当a1=3时，不合题意;

当a1=2时，当且仅当a2=6,a3=18时，符合题意;

当a1=10时，不合题意.

因此a1=2,,a2=6,a3=18.

所以，等比数列{an}的公比q=3，故an=2·3n-1.

例2已知数列{an}，其中a1=1，an+1=2an+3n+1，求数列{an}的通项公式.

分析题干明显存在递推公式，递推公式的类型是an+1=Aan+B·cn+D，所以根据解题模块确定可以运用构造法解题.

解法1设存在实数λ，使得an+1+λ·3n+1=2(an+λ·3n)，即an+1=2an-λ·3n，所以λ=-3，则有an+1-3n+2=2(an-3n+1).令bn=an-3n+1，因为a1=1，所以数列{bn}是一个首项为-8 ，公比为2的等比数列，所以an=3n+1-2n+2.

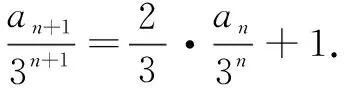
点评本题的两种解法采用了不同的构造方式，但最终的目的都是通过构造等比数列,间接地求解通项公式．需要说明的是,在求解数列通项公式问题时,构造方法可能不唯一,可以根据递推公式的形式创造性地构造．待定系数法是构造数列的常用方法,可以通过求解未知系数确定需要构造的形式.

例3(2019年江苏高考题) 定义首项为1且公比为正数的等比数列为“M-数列”.

(1)已知等比数列{an}(n∈N*)满足:a2a4=a5,a3-4a2+4a1=0,求证:数列{an}为“M-数列”;

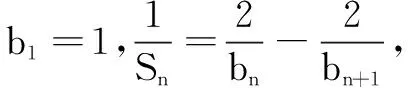
① 求数列{bn}的通项公式;② 略．

分析第(1)问直接验证．第(2)问的题干条件存在递推公式,递推公式是关于数列{bn}及其前n项和Sn的关系式.所以求数列{bn}通项公式的基本思想是利用

来求解.

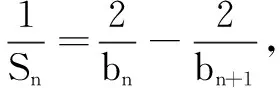
点评求解本类含有数列及其前n项和关系式的数列通项公式问题时,需要把握住解题的关键.就是利用

进行求解.需要注意的是,不要忘记n=1的情况.当a1不满足Sn-Sn-1求出的公式时,通项公式应写成分段形式.

四、结语

数学问题的解决离不开个人解题能力的支撑，而解题能力离不开数学知识和已有的数学认知结构的支撑.本文通过对数列通项公式问题的探索，将题目条件、形式、方法进行归类，系统地建立了数列通项公式问题的数学认知结构，运用这个解题模块，可以看到它在部分数列通项公式求解问题解决中的作用．当然,并不是每一类问题都可以建立解题模块，对于不能建立解题模块的数学问题，我们能否建立问题的命题联想系统,解题模块和命题联想系统之间有什么联系和差异等问题，还有待于进一步研究.