三个理解视角下运算能力的提升

韩 帆

(浙江省杭州市萧山区第十一高级中学，311200)

数学运算能力是指在明晰运算对象的基础上,依据运算法则、解决数学问题的素养，是数学核心素养的重要组成部分．

《普通高中数学课程标准(2017年版)》对数学运算能力的基本要求是能够了解运算法则及其适用范围,正确进行运算,能够根据问题的特征形成合适的运算思路,在此基础上能够针对运算问题,合理选择运算方法，设计运算程序,运算求解．通过高中数学课程的学习,学生能进一步发展数学运算能力,有效借助运算方法解决实际问题．通过运算能促进学生数学思维发展,形成规范化思考问题的品质, 养成一丝不苟、严谨求实的科学精神． 而“理解数学,理解学生,理解教学”是课改的三大基石.笔者结合平时教学中碰到的问题,从三个理解的角度谈谈怎样提升学生的运算能力．

一、理解数学

理解数学不仅是针对教师,更重要的是使学生在老师的帮助下理解数学．例如对数的运算性质,许多学生对对数的运算公式的适用范围,运算法则模糊不清,甚至想当然地自己创造出logaM·logaN=loga(M·N)，loga(M+N)=logaM+logaN之类的运算公式．那么怎样更好地帮助学生来理解算法和算理呢?首先要让学生了解对数的来历．对数是一种运算,从小学到初中,学生已经学习了加减乘除,乘方开方,那还要对数干什么呢?刚刚进入这一节新内容时教师就应该讲清楚对数的前世,是自然科学领域(特别是天文学)的发展推动了对数的问世,正是为了简化大量繁琐的运算,数学家们发明了对数．对数的运算又是怎样的呢?有了之前的铺垫,用指数运算来推导对数运算法则的过程就水到渠成了．有的教师在对数的运算这一节当中,会轻推理证明,重公式记忆和操练,试图通过重复训练达成教学目标．短时间大强度的训练或许可以暂时提高运算的速度和准确率,但不是长久之计．知识没有理解,没有内化到头脑中,终究只是简单的依样画葫芦，最后连这个“样”也会随着时间渐渐遗忘．

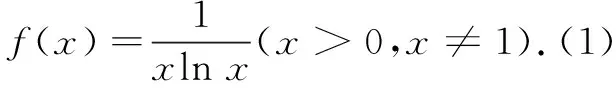
二、理解学生

章建跃博士提出三个理解时,把“理解学生”放在“理解教学”之前.可见，只有掌握学情才能采取有效教学策略．所以我们要找到学生的“最近发展区”,在尊重学生认知结构的基础上实现质的飞跃．

例如，学生在面对解析几何题时,常常 是“思路对,算不出”．那教师就要仔细分析学生出问题的点,从学生的角度来考虑,关注学生怎么想,而不是埋头算给学生看．

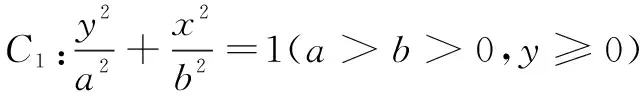
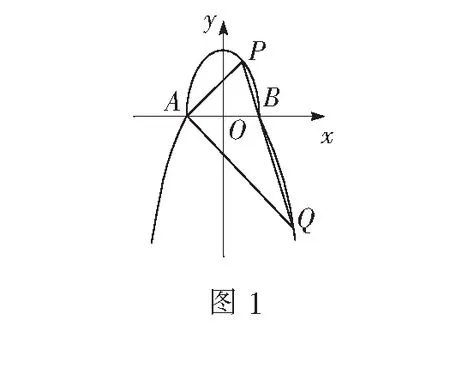
(1)求a,b的值;

(2)过点B的直线l与C1,C2分别交于点P,Q(P,Q,A,B中任意两点均不重合),若AP⊥AQ,求直线l的方程.

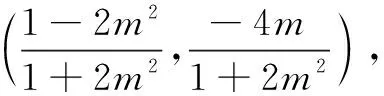
该题直线方程的设法通常有两种．除了这里设x=my+1(m≠0)外,还可把直线方程设为y=k(x-1)．不难理解,后一种设法在学生的脑海里更是根深蒂固．因为在讲直线方程几种形式的时候,第一个遇到的就是它，在平时解题中,用得比较多的也是它．所以不能急着否定这种设法,而应该和学生一起继续计算下去．第二个就是方程联立,应用韦达定理以后,学生只知道“设而不求”这句话,却不知它的深意．仔细分析可知,在这题中,直线与椭圆两个交点中的一个是已知的,那另一个自然就可以轻松算出来啦．了解到这些，当然是x=my+1(m≠0)这种直线方程的设法更好，减少了计算量．让学生再用这种方式自己算一遍,就能让他们体会到区别,从而今后能合理选择运算的对象,提高运算的速度和准确率．

三、理解教学

理解了学生,才能有效地组织教学．而课堂教学也不是预设的简单执行,而是在课堂上重新生成、不断组织的过程，是学生不断发展,提升的过程．那么，在平时的教学过程中，怎样才能让学生乐于思考,勤于动笔,不断提升他们的运算能力呢?这是一个长期的过程，要培养学生的运算能力,要特别重视课堂练习.数学运算能力提高的主阵地是课堂，教师不能自顾自算自己的,或者直接在课件上呈现运算结果,这很容易导致学生“一听就会,一做就错”．教师要指导学生如何计算,教给学生基本的方法,不能越俎代庖．要求学生要心算,也要笔算．哪些步骤可以心算,不需要浪费时间写下来,哪些步骤一定要清楚地写下来,不能偷懒．这些都需要老师在平时的课堂中不断启发学生．要求学生运算中的草稿也要整洁,因为草稿不是“潦草”．整洁的草稿不仅反映了清晰的思维,而且还能快速查找出错误步骤所在,节约检查验算的时间．另外,学生的心理因素的影响也不可忽视．常常会听到有学生抱怨“这题太复杂,看得头都大了”.对这样的同学要多加鼓励和引导,培养其信心．还要帮助“这题太简单,一看就知道答案”的同学沉下心来,培养细心和耐心,避免常识性错误．比如下面这道题.

例3不等式cos 2x-4sinx-a<0有解,则实数a的取值范围是______.

不少同学拿到题后,觉得这简单呀,立马开始计算.

∵cos 2x-4sinx-a<0，

∴1-2sin2x-4sinx-a<0.

令sin2x=t，则-2t2-4t+1-a<0.由Δ<0,就可以求出a．完全忽视了sinx的范围．对于这样的同学,在平时就要培养他的耐心,细心和考虑问题的全面性就至关重要了．

如果能踏踏实实做好上面三个理解,那么学生数学运算能力和水平的提升就指日可待．正所谓静待花开,芬芳自来．