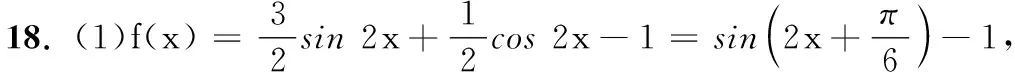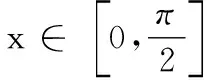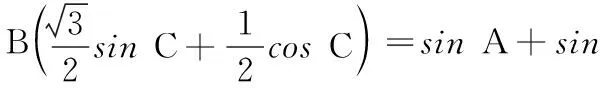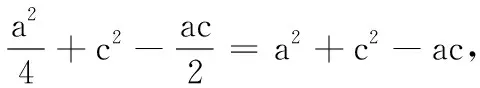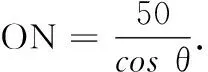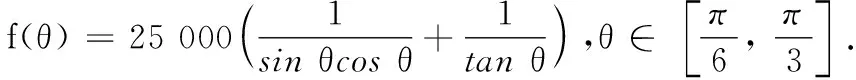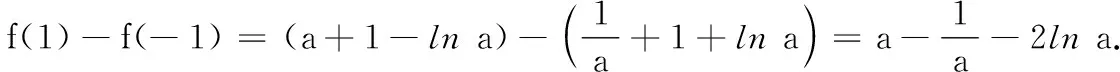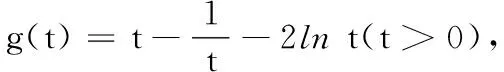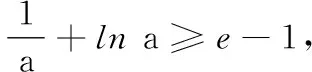高二数学测试
一、单项选择题(本大题共8小题,每小题5分,计40分)
1.已知集合M={y|y=2x,x>0},N={x|y=lgx},则M∩N为( )
(A)(0,+∞) (B)(1,+∞)
(C)[2,+∞) (D)[1,+∞)

(A)1 (B)-1 (C)i (D)-i
3.已知f(x)是定义在R上的奇函数,当x≥时,f(x)=3x+m(m为常数),则f(-log35)的值为( )
(A)4 (B)-4 (C)6 (D)-6



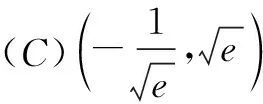
二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错的得0分)
9.下列命题中,正确的是( )
(A)在∆ABC中,若A>B,则sinA>sinB
(B)在锐角三角形ABC中,不等式sinA>cosB恒成立
(C)在∆ABC中,若acosA=bcosB,则∆ABC必是等腰直角三角形
(D)在∆ABC中,若B=60°,b2=ac,则∆ABC必是等边三角形

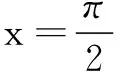
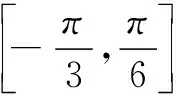
(C)f(x)最小正周期为π

11.下列叙述中正确的是( )
(A) 若a,b,c∈R,则“ab2>cb2”的充要条件是“a>c”
(B) “sinα=cosα”是“cos 2α=0”的充分不必要条件
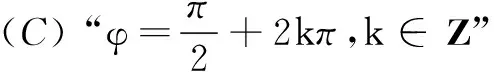
(D) i是虚数单位,a,b∈R,则“a=b=1”是“(a+bi)2=2i”的充分不必要条件
12.若定义域为(0,+∞)的函数f(x)的导函数f′(x)满足xf′(x)+1>0,且f(1)=1,则下列结论中成立的是( )
(A)f(e)>0
(C)∀x∈(1,e),f(x)>0
三、填空题(本大题共4小题,每小题5分,计20分)
13.如图,一辆汽车在一条水平的公路上向正西行驶,到A处时测得公路北侧一山顶D在西偏北30°的方向上,行驶600 m后到达B处,测得此山顶在西偏北75°的方向上,仰角为30°,则此山的高度CD=______m.


15.在锐角三角形ABC中,已知sinC=4cosAcosB,则tanAtanBtanC的最小值为______.

四、解答题(本题共6小题,共70分.解答时写出必要的文字说明,证明过程或演算步骤)
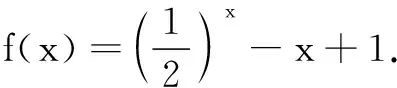
(1) 设f(x)的值域为A,求集合A;

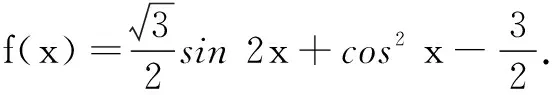


19.(本小题满分12分)在∆ABC中,角A,B,C的对边分别为a,b,c,且满足
(1)求角B的大小;
(2)若点M为BC中点,且AM=AC,求sin∠BAC.
20.(本小题满分12分)已知二次函数f(x)为偶函数且图象经过原点,其导函数f′(x)的图象过点(1, 2).
(1)求函数f(x)的解析式;
(2)设函数g(x)=f(x)+|f′(x)-m|,其中m为常数,求函数g(x)的最小值.
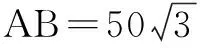
(1)求f(θ)关于θ函数关系式,并写出定义域;
(2)为节约投入成本,当tanθ为何值时,总费用f(θ)最小?

22.(本小题满分12分)已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)求证:f(x)在(0,+∞)单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
参考答案
一、单项选择题
1.B;2.D;3.B;4.C;
5.D;6.D;7.A;8.B.
二、多项选择题
9.ABD;10.BC;11.BD;12.ABC.
三、填空题
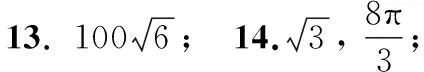
四、解答题
17.(1)由f(x)是定义在R上的偶函数,可得f(x)的值域A即为x≥0时f(x)的取值范围.
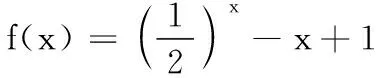
(2)函数g(x)的定义域为B={x|-x2+(a-1)x+a≥0}={x|(x-a)(x+1)≤0}.
若a<-1,则B=[a,-1],显然满足B⊆A;
若a>-1,则B=[-1,a],要使B⊆A,则需a≤2,此时-1 当a=-1,则B={-1},满足B⊆B. 综上,a的取值范围为(-∞,2]. (2)解法1取CM中点D,连AD,则AD⊥CM,则CD=x,BD=3x. 在∆ABM与∆ABC中,由余弦定理,分别得 AC2=a2+c2-2accosB =a2+c2-ac. 20.(1)由f(x)图象经过原点,可设f(x)=ax2+bx(a≠0). 依题意,x∈R,f(-x)=f(x),即a(-x)2+b(-x)=ax2+bx,即2bx=0对任意实数x∈R都成立,故b=0. 所以f(x)=ax2,f′(x)=2ax,由f′(x)的图象过点(1, 2),得2a×1=2,解得a=1. 所以f(x)=x2. (2)由(1)知g(x)=x2+|2x-m|,即 f(θ)=20S∆OMN+500AM (2)由(1)可知 22.(1)f′(x)=2x+(ax-1)lna,易见当x∈(0,+∞)时,(a2-1)lna>0,得f′(x)>0,f(x)在(0,+∞)单调增. (2)由f′(0)=0,且f′(x)在R上单调增,可知f′(x)=0有唯一解x=0,且x<0时,f′(x)<0,f(x)单调减;x>0时,f′(x)>0,f(x)单调增.从而f(x)在x=0取极小值1. 又函数y=|f(x)-t|-1有三个零点,所以方程f(x)=t±1有三个根.而t+1>t-1,所以t-1=(f(x))min=f(0)=1,解得t=2. (3)依题意,当x∈[-1,1]时,|(f(x))max-(f(x))min|=(f(x))max-(f(x))min≥e-1. (i) 当a>1时,由f(1)-f(0)≥e-1,得a-lna≥e-1可得a≥e.