新定义型数列题分类赏析*
宁永楠 武瑞雪
(江苏省睢宁县第一中学,221200)
新定义型数列题不局限于课本上的等差、等比两类数列去命题,而是给出一个新定义的数列,然后按照这个新定义去解决相关问题的一类题目.这类题目具有一定的挑战性、新颖性、区分性和选拔性,有利于考查学生的阅读、理解、类比、迁移等能力,有利于考查学生思维的深刻性、批判性和创新性等学习潜能,帮助学生克服机械学习过程中形成的“懂而不会,会而不对”等现象,有效提高学生的学习兴趣,培养解题过程中的科学思维的习惯.
一、 以函数性质为背景
例1(1)在一个数列中,如果每一项与它的后一项的和为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列{an}是等和数列,若a1=2,公和为5,那么a18的值为______,前21项和S21的值为______.
(2)在一个数列中,如果每一项与它的后一项的积为同一个常数,那么这个数列叫做等积数列,这个常数叫做该数列的公积.已知数列{bn}是等积数列,若b1=2,公积为5,Tn为数列的前n项积,则T2 020=______.
解(1)细心计算,易得此数列为2,3,2,3,2,….{an}以2为周期,故a18=a2=3,S21=5×10+2=52.
….{bn}也以2为周期,前2 020项积为1 010个5相乘,即T2 020=51 010.
评注数列是一种特殊的函数,对周期数列可类比周期函数进行理解.本题在实际教学中,可进一步引导学生探究等和数列、等积数列的通项公式、递推关系式及前n项和公式(限于篇幅,这里从略);并与等差数列、等比数列的相关内容进行对比,以培养学生的类比、迁移、创新、探究、分析新问题、解决新问题的能力.
例2已知数列{an},从中选取第i1项,第i2项,…,第im项,若ai1 解aim的下标中还有下标,理解了此式以及“递增子列”的定义,并能注意思考顺序,就不难写出满足题意的长度为4的所有递增子列:1,3,5,6;1,3,5,8;1,3,6,8;1,5,6,8;3,5,6,8. 又由条件(2),可得b5=5,且|a5-b5|≤20,即|a5-5|≤20,解得-15≤a5≤25. 所以,a5的取值范围是[16,25]. 评注本题需在理解新数列定义的基础上,抓住特殊与一般的关系解决问题. 例4如果一个数列的各项都是实数,且从第二项起,每一项与它前一项的平方差是同一个的常数,则称该数列为等方差数列,这个常数叫做这个数列的公方差. (1)若数列{an}既是等方差数列,又是等差数列,证明:数列{an}为常数列; (2)若数列{an}是首项为2,且各项为正,公方差为2的等方差数列,求数列{an}的通项公式. 分析本题由“等差数列”的定义类比给出“等方差数列”的定义,只要能透彻理解等差数列、等方差数列定义,再注意对公差d是否为零进行讨论,熟悉“累加法”的适用条件,问题将迎刃而解. 又由{an}是等差数列,设an-an-1=an+1-an=d.若d≠0,则由上可知an+an-1=an+1+an,即an-1=an+1,这与d≠0矛盾,所以d=0,即数列{an}为常数列. 分析如何理解和利用新定义数列提供的条件是顺利解答此题的关键. anlgxn=an+1lgxn+1=an+2lgxn+2=p. ① 例6设数列{an}的前n项和为Sn,若对任意正整数n,总存在正整数m,使得Sn=am,则称{an}是“H数列”.现给定数列{bn},其前n项和Tn=2n(n∈N*),求数列{bn}的通项公式,并证明{bn}是H数列. 解由条件可知,当n=1时,b1=T1=2;当n≥2时,bn=Tn-Tn-1=2n-1. 由通项公式可知,对任意正整数n,当n=1时,存在m=n=1,使Tn=bm;当n≥2时,存在m=n+1,使Tn=bm,所以{bn}是H数列. 评注本题以简易逻辑为背景,考查学生对“H数列”定义的理解,同时也考查数列的通项与前n项和之间的关系解题时要分n=1和n≥2两种情况讨论,然后再看能否合并统一. 例7已知{an}是各项非负的单调增数列,对于正整数K,若对任意1≤i≤j≤K,其中i,j∈N*,有aj-ai仍是{an}中的项,则称数列{an}为“K项可减数列”. (1)已知{an}是首项为2,公比为2的等比数列,且数列{an-2}是“K项可减数列”,试确定K的最大值; 解(1)设cn=an-2=2n-2,则c1=0,c2=2,c3=6,易得c1-c1=c1,c2-c1=c2,c2-c2=c1,则{cn}一定是“2项可减数列”. 又c3-c2≠c1,c3-c2≠c2,c3-c2≠c3,所以K的最大值为2. (2)由{an}是“K项可减数列”,得aK-at(t=1,2,…,K) 必是数列{an}的项;又{an}单调增,故aK-aK 评注第(1)问只要学生理解“K项可减数列”的定义,并充分利用题目中条件,则易得解;在第(2)问中,不仅要紧扣新概念,还要掌握数列求和的相关基础知识、基本方法,综合性较强. 由上可见,新定义型数列题并不一定是“难题”,只要有扎实的基础知识、基本技能、基本思想、基本活动经验、良好的心理素质,擅于深入地分析、仔细地观察、认真地归纳、合理地迁移,能透过“新”现象看出“旧”本质,能撩开“新”面纱,定能顺利解决.

二、以熟悉的数列、级数为背景
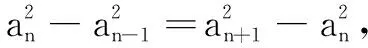

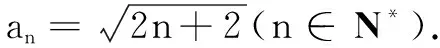


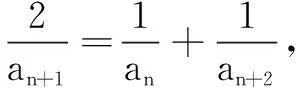
三、以简易逻辑为背景

四、 以运算的封闭性为背景的新数列




