例谈多元不等式恒成立问题的解题策略

田长青

(江苏省扬州市第一中学，225001)

不等式是高中数学的重要内容,不等式恒成立问题在各类考试中经常出现,它往往与多个知识点交汇,具有一定的综合性.有些不等式恒成立问题中含有多个变量,使题目显得繁杂且对思维灵活性要求较高,学生往往难以找到解决问题的突破口.本文结合教学实例,探讨某些多变量不等式恒成立问题的解题策略.

一、整体分析,变换消元

对某些多变量不等式恒成立问题,若变量x，y之间联系比较紧密,可通过恒等变形,先将不等式转化为关于m(x,y)的表达式(其中m(x,y)为x，y组合成的表达式),再通过换元法转化为“一变一参”的问题.

例1对于任意的正数a，b,不等式(2ab+a2)k≤4b2+4ab+3a2恒成立,则k的最大值为______.

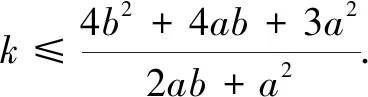
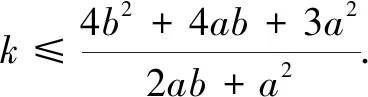
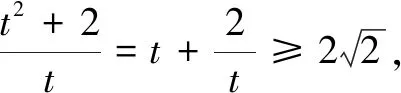
例2(2010年湖南高考题)已知函数f(x)=x2+bx+c(b，c∈R),且对任意的x∈R,恒有f′(x)≤f(x).

(1)证明:当x≥0时,f(x)≤(x+c)2;

(2)若对满足题设的任意b，c,f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.

解(1)略.

(2)由(1)知,c≥|b|.

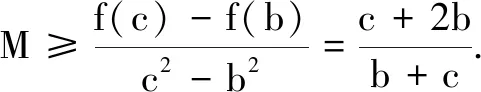
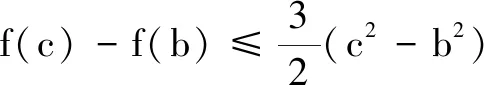
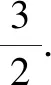
二、逐步分析,确定主元

对有些多变量不等式恒成立问题,在不便于消元的情况下,可以把其中一个变量先看成主变量,其它字母都看成参数.先解决主变量恒成立问题,再把另一个变量看成主变量,通过逐步分析步步逼近,最后求得结果.

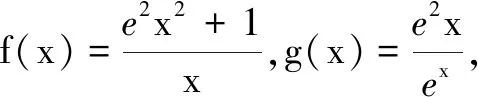
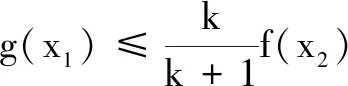
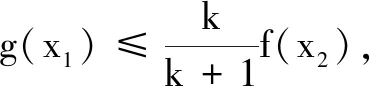
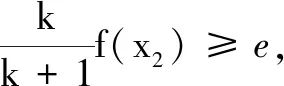
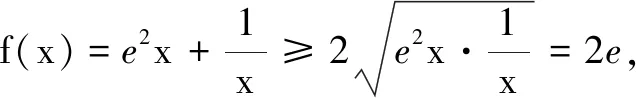
例4若对任意k∈[-1,1],当x∈(0,4]时,不等式6lnx+x2-9x+a≤kx恒成立,则实数a的最大值是______.

分析本题中有两个变量k，x,一个参数a.与例3类似,可以先把变量k看成主变量,再把变量x看成主变量,通过两次求一元函数最值,即可求出实数a的取值范围.

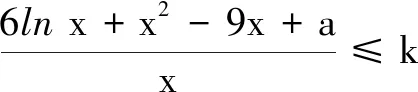
于是,不等式a≤-6lnx-x2+8x在x∈(0,4]恒成立.令f(x)=-6lnx-x2+8x,x∈(0,4],则a≤f(x)min.

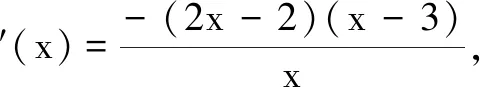
综上,a≤7,即实数a的最大值为7.

三、特征分析,数形结合

例5已知不等式(m-n)2+(m-lnn+λ)2≥2对任意m∈R,n∈(0,+∞)恒成立,则实数λ的取值范围为______.

分析本题用以上两种方法皆难以完成,观察表达式的代数特征,联想其几何意义,代数式(m-n)2+(m+λ-lnn)2表示点P(m,m+λ)与点Q(n,lnn)之间的距离的平方,可将代数问题转化为几何问题来解决.

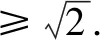
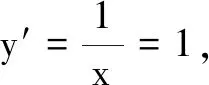
多变量不等式恒成立问题呈现形式多样,解题方法灵活多变,技巧性较强.要求我们从不同的角度、不同方向分析探讨,选择适当的方法解题.当然,除了以上的方法外,还有许多其它的方法等待我们去总结,需要同学们在具体的解题过程中充分发挥自己的主观能动性.要感悟数形结合、转化与化归、函数与方程、整体代换等数学思想的运用；体会数学建模、逻辑推理、数学运算、直观想象等核心素养.综合考虑,灵活运用,才能使问题得以顺利解决.