非均匀土中渐变摩擦桩的失稳分析

邵先锋, 陈曦鸣, 杨泰朋, 李 凯

(1.国网安徽省电力有限公司建设分公司,安徽 合肥 230022; 2.安徽送变电工程有限公司, 安徽 合肥 230001; 3.安徽建筑大学 土木工程学院, 安徽 合肥 230601)

0 引 言

在地质工程设计中,细长桩的屈曲失稳是一个需要重点考虑的问题,尤其在细长桩埋于软弱土层的情形下。大量研究表明,当细长桩嵌入在软土层、受侵蚀土及液化土中时,屈曲破坏很有可能发生[1-4]。此外,随着高承载力桩在实际工程中的大量应用,完全嵌入桩在桩截面屈服前也可能发生屈曲失稳[3]。

对于桩的屈曲响应行为,相关研究成果较丰富。文献[5]通过采用弹性地基上梁的稳定性方法研究了侧向弹性地基支承桩屈曲问题;文献[6]给出了两端铰支桩的屈曲荷载解析解;文献[7-8]研究了部分嵌入和桩端不同自由度约束对桩屈曲行为的影响;文献[9]将能量方法应用于桩屈曲承载力分析;文献[10]使用尖点突变理论构建数学模型分析桩的屈曲荷载;文献[11]推导了修正Vlasov地基模型支承下的桩失稳方程,并利用振动方法给出了数值屈曲解;文献[12]考察了固定体积时变截面形状对屈曲的影响;文献[13]考虑桩-土摩擦作用对桩屈曲的影响,采用地基反力法理论,应用最小势能原理研究了各种边界条件下摩擦基桩屈曲行为。

虽然上述研究考虑了桩-土作用对细长桩屈曲行为的影响,但是综合考虑非均匀侧向支撑和非均匀侧摩阻力对渐变摩擦桩屈曲失稳行为影响的研究很少。本文考虑了沿深度方向线性变化的基床反力和侧摩阻力,建立非均匀土中渐变摩擦桩屈曲理论模型,推导3类典型边界条件下完全嵌入渐变桩的平衡微分方程,并编制基于bvp4c算法的Matlab程序对屈曲特征值问题进行了数值求解,详细讨论了桩-土体系多个几何及物理参数对桩屈曲行为的影响规律。

1 公式推导

1.1 桩-土系统平衡微分方程

在直角坐标系下建立长为L的竖直完全嵌入桩,以竖直方向为x轴,水平方向为y轴,完全嵌入桩示意图如图1所示。考虑均质弹性圆截面桩,桩径沿着x方向线性变化,变化公式为:

图1 非均匀土中完全嵌入渐变桩示意图

(1)

其中,m为截面渐变率,m=rb/rt,rb为桩端面半径,rt为桩顶面半径。任意桩长深度处的桩径可表示为:

rx=txrt

(2)

其中,rx为深度x处的桩截面半径。为了推导方便,给出桩长中点处的桩径为:

(3)

(4)

对于完全嵌入桩,采用基床反力系数为线性增加的弹性Winkler地基来反映非均匀土层侧向刚度。随深度变化的基床反力系数k可表示为:

k=ktHx

(5)

(6)

其中,n为基床反力系数比,可用来反映土层侧向刚度的不均匀性,n=kb/kt,kb、kt分别为桩端和桩顶处水平基床反力系数。

类似地,考虑桩侧摩阻力系数f也随深度线性变化,变化公式为:

f=ftZx

(7)

(8)

其中,z为侧摩阻力系数比,可用来反映桩-土间侧摩阻力的不均匀性,z=fb/ft,fb、ft分别为桩端和桩顶处侧摩阻力系数。

为了推导方便,定义桩长中点处的基床反力系数k0和侧摩阻力系数f0分别为:

(9)

其中,n1=n+1；z1=z+1。利用(5)～(9)式可以将k和f重新表示为:

(10)

取隔离体微段如图1b所示,桩顶施加轴向荷载P,桩端受到反力Pb。桩微段平衡方程为:

(11)

(12)

(13)

其中,N为桩轴力;V为剪力;M为弯矩。利用桩弯矩-曲率关系M=EId2y/dx2,其中E为桩的弹性模量,将(11)～(13)式合并为一个桩-土系统下的四阶常微分方程,即

(14)

N与P关系为:

(15)

将(4)式代入(15)式并积分可得:

(16)

其中,m2=m-1；z2=z-1。

为了得到无量纲化方程以方便讨论参数影响,引入如下无量纲化变量:

(17)

利用无量纲化变量将(14)式变形为:

(18)

其中,p=x′+(m2+z2)x′2/2+m2z2x′3/3；s=1+(n-1)x′；t=1+(z-1)x′；c=1+m2x′。当外荷载引起的轴力到达临界屈曲内力时,屈曲失稳发生。

1.2 3类典型边界条件下的微分方程

(1) 两端自由的边界条件。在x′=0处,有

(19)

在x′=1处,有

(20)

(2) 一端自由、一端铰支时的边界条件。在x′=0处,有

(21)

在x′=1处,有

(22)

(3) 一端自由、一端固支时的边界条件。在x′=0处,有

(23)

在x′=1处,有

(24)

1.3 屈曲应力

对于渐变桩,无量纲化桩屈曲应力定义为:

(25)

(26)

2 数值结果和讨论

本文利用bvp4c算法,编制Matlab程序,求解一系列参数组合时的屈曲荷载因子b,给出了b随不同参数的变化规律。在计算中,根据实际工程中的典型数据给出如下参数[14]:

r0=0.5 m,L0=2.5 m,E=10 GPa,

k0=10 MN/m3,f0=100 kPa。

相关无量纲量范围如下:截面渐变率m为0～1;基床反力系数比n为0～10;侧摩阻力系数比z为0～10;桩-土相对刚度α为0～10;无量纲化侧摩阻力系数β为0～0.05。无量纲化桩径D′与α相关。3种典型边界条件下,n对b的影响规律如图2所示。

图2 3种典型边界约束下n对b的影响

由图2可知,不论哪种边界条件下,b均随着n增大而减小,即土层越不均匀越易失稳。3类边界条件下函数曲线态势相似,其中一端自由、一端固支的情况下,变化率最大,而两端自由的桩,变化相对平缓。该结果表明,约束越强,b越大。

不失一般性,在以下研究中边界条件选定为一端自由、一端固支,以突出相关参数对桩屈曲行为的影响。n取值为1.0、2.5、5.0时,m对b的影响如图3所示。由图3可知,不同土层非均匀性下曲线的变化态势是相似的,m从0变化到0.2时,对b的影响显著,且基本呈线性增长关系;m为0.2～0.4时,对b的影响较为平缓,但仍是正相关;之后随着m增大,b逐渐减小。该结果表明,存在一个对应于最大b的最优m,此时桩具有最强承载能力。此结果可为优化渐变桩截面设计提供指导。

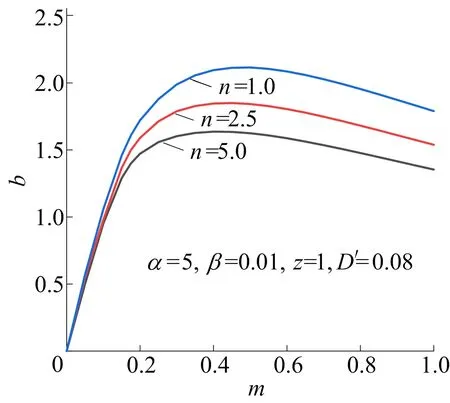
图3 n不同时m对b的影响

n取值为1.0、2.5、5.0时,β对b的影响规律如图4所示。由图4可知,b与β之间近似呈线性关系,并且b随着β增大也相应增大。该结果表明,β较大时,其对桩的屈曲载荷的影响应加以考虑。此结果可用于精确预测摩擦桩承载能力。

图4 n不同时β对b的影响

n取值为1.0、2.5、5.0时,α对b的影响曲线如图5所示。由图5可知,随着α增大,b显著增大。该结果表明,土层的刚度对桩临界失稳荷载因子影响显著。因此,桩基设计时,除了考虑土层本身的物理力学参数,还可采用施工技术改变土层的综合刚度,进而提高桩屈曲荷载。

图5 n不同时α对b的影响

n取值为1.0、2.5、5.0时,z对b的影响曲线如图6所示。由图6可知,随着z增加,b减小并趋于稳定;反之,z减小,b增大。因此,为明显提高b值,应使桩侧摩阻力系数随深度快速减小。

图6 n不同时z对b的影响

n取值为0.5、1.0、5.0、10.0时,横截面上屈曲应力σb沿深度的变化规律如图7所示。

图7 n不同时σb沿深度的变化规律

由图7可知,n较大时,屈曲应力自桩顶往下单调减小,最大应力发生在桩顶处;而n较小时,屈曲应力自桩顶往下单调增加,最大应力发生在桩底处。该结果表明,土层非均匀性显著改变屈曲应力分布规律,也显著改变危险截面位置。此结果预测的危险截面位置可为工程桩的加固提供理论指导。

3 结 论

本文研究了非均匀土层中渐变摩擦桩的屈曲问题,建立了考虑非均匀基床反力和侧摩阻力的理论模型,基于推导的四阶微分方程,编制基于bvp4c算法的Matlab程序进行了求解。结果显示,基床反力系数比n、截面渐变率m、无量纲化侧摩阻力系数β、桩-土相对刚度α等对屈曲荷载因子b有重要影响,土层非均匀性显著改变屈曲应力分布规律和危险截面位置。本文提出的研究方法和结果可以用来评估桩失稳荷载的变化态势,进而可通过控制参数达到设计、施工的要求,为实际工程提供指导和建议。