基于神经网络路面识别的电动汽车ABS控制研究
王国微, 尹安东
(合肥工业大学 汽车与交通工程学院,安徽 合肥 230009)
0 引 言
制动防抱死系统(anti-lock braking system,ABS)是车辆主动安全性的重要保证,该系统能使车辆充分利用路面附着能力,有效避免车辆甩尾和失去转向能力,保证车辆的行驶安全[1]。对电动汽车来说,制动过程中驱动电机参与制动并进行制动能量回收,这对续驶里程受限的电动汽车来说具有重要意义,因此在保证制动安全的前提下尽可能多的回收制动能量是电动汽车ABS控制急需解决的问题[2]。
目前ABS控制方法有逻辑门限值控制、模糊控制、神经网络控制、滑模控制等[3-4],其控制目标是将实际滑移率维持在最优滑移率处,以使车辆充分利用路面附着能力,因此准确估算当前路面最优滑移率尤为重要。通常估算最优滑移率的方法有:① 根据附着系数-滑移率(μ-λ)曲线斜率估算[5];② 通过检测仪器识别路面材质估算路面最优滑移率[6];③ 运用模糊理论进行路面识别[7-8]等。通过μ-λ曲线斜率进行识别需要的数据较多,实时性差;通过仪器检测路面的方式准确度较高,但经济性差;模糊识别精度依赖于规则制定,识别结果不稳定。
本文提出一种基于径向基函数(radial basis function,RBF)神经网络识别路面的方法,在ABS控制策略下调整制动力矩,并制定制动力矩分配策略,将实际滑移率维持在最优滑移率处,从而充分利用路面附着能力并实现制动能量回收,最后进行实例样车仿真分析。
1 制动时轮胎受力分析
良好硬路面上汽车制动时轮胎受力[9]情况如图1所示。其中,va为轮心速度;Tb为车轮制动器摩擦力矩;Fxb为地面制动力;W为车轮竖直载荷;Fp为车轴对车轮的推力;Fz为地面对车轮的法向反作用力。
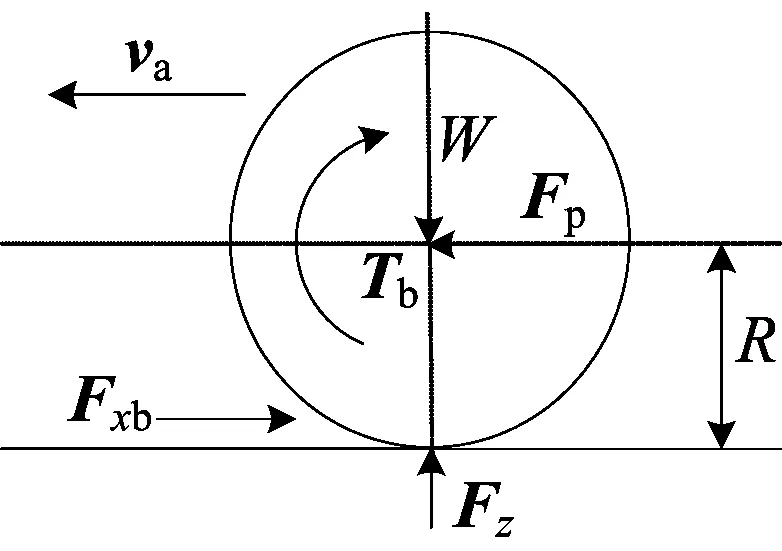
图1 制动时轮胎受力情况
对车轮受力分析可得其运动方程为:
(1)
Fxb=μFz
(2)
其中,J为车轮转动惯量;ω为车轮角速度;μ为轮胎与路面间的纵向利用附着系数。
随着制动强度增大,地面附着能力逐渐不足以提供车辆所需的制动力,增加滑移成分,滑移程度由滑移率表征,滑移率λ定义如下:
(3)
2 μ-λ曲线模型
Burckhardt提出的μ-λ曲线模型[10]如下:
μ(λ)=c1(1-e-c2λ)-c3λ
(4)
对(4)式进行数学解析可以得到路面的最优滑移率λopt和路面峰值附着系数μmax为:
(5)
(6)
其中,c1、c2、c3为各路面的参数值。
不同路面条件下指数函数模型各参数值见表1所列,由表1所列数据绘制的μ-λ曲线如图2所示。

表1 不同路面条件下指数函数模型各参数值
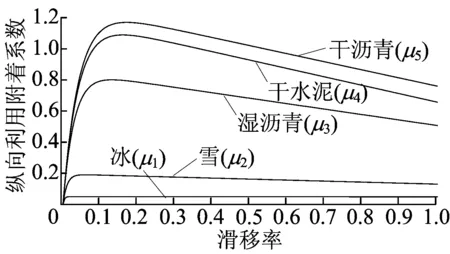
图2 标准路面μ-λ曲线
3 神经网络路面识别方法
3.1 标准路面区域划分
首先,结合图2构造4条辅助线,辅助线数据计算公式为:
(7)
其中,μLi为第i条辅助线;μi为第i条标准路面μ-λ曲线。
辅助线μL2所在区域与湿水泥路面吻合,且μ2路面与μ4路面之间跳变过大,为增强适用性,这里构造辅助线μL5、μL6,将其所围区域作为湿水泥路面。最终划分结果见表2所列,具体区域如图3所示。μL5、μL6的计算公式为:
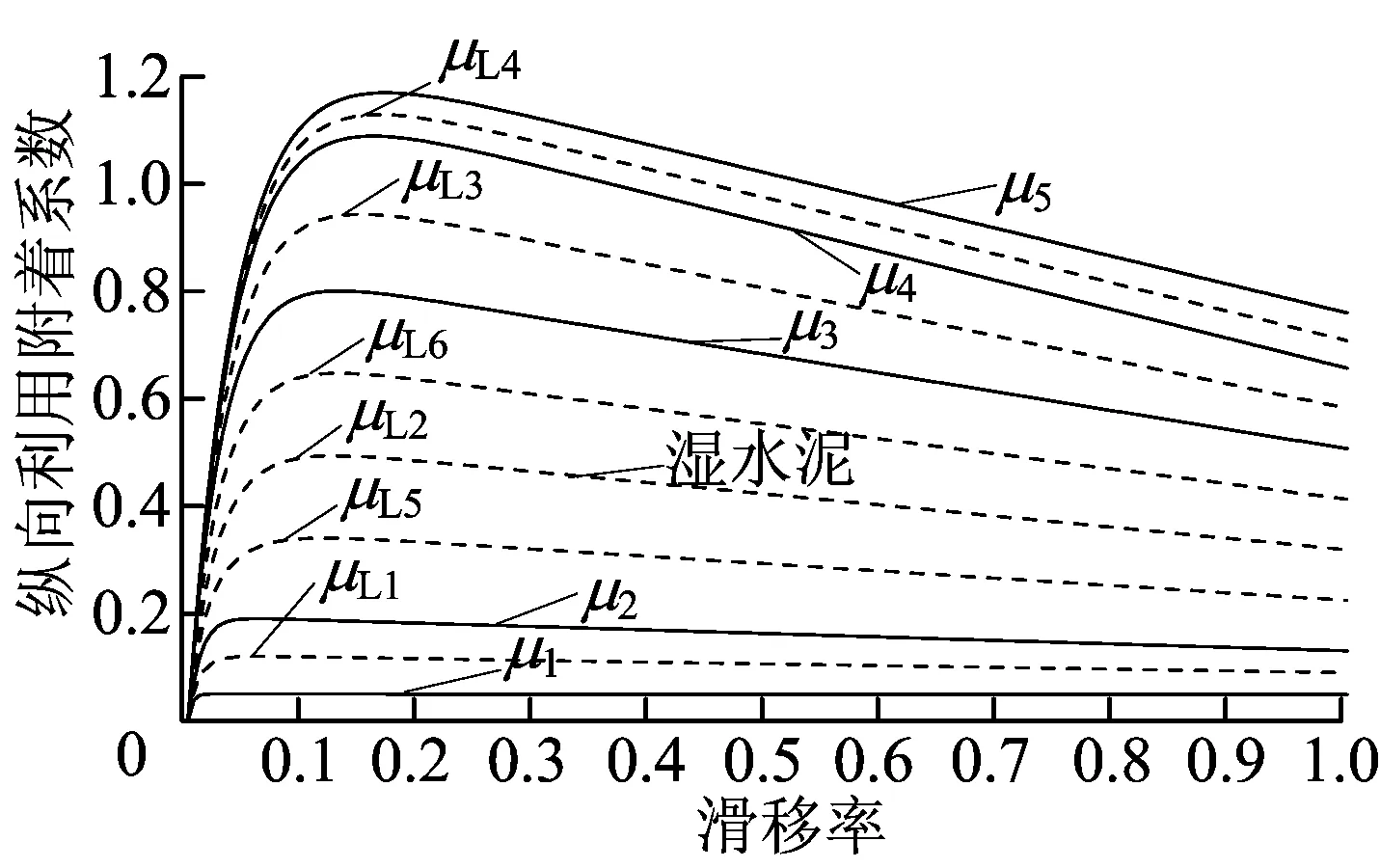
图3 各种路面区域划分
μL5(λ)=[μ2(λ)+μL2(λ)]/2,
μL6(λ)=[μL2(λ)+μ3(λ)]/2
(8)

表2 标准路面区域划分及识别编号
根据λ与μ判断路面处于其中某个区域,即对应某条标准路面,从而得到λopt、μmax。在这种非凸域分类方面,RBF神经网络优势明显,它是局部逼近的单隐层前向网络,分类能力强、收敛快。因此采用RBF神经网络[11-12]进行区域分类识别。
3.2 RBF神经网络路面识别过程
将λ、μ作为RBF神经网络输入层的2个节点参数,输出层有1个节点,其值y对应标准路面区域号。拓扑结构如图4所示。其中,φi为第i个隐层节点输出;wi为第i个隐层节点与输出节点间的连接权值。
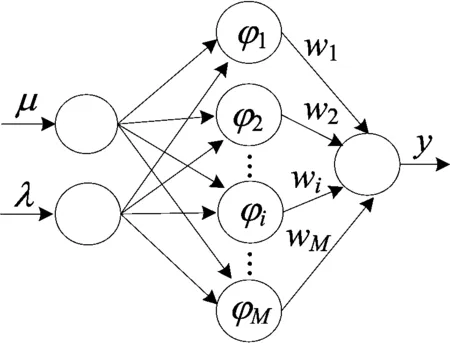
图4 两参数输入RBF神经网络拓扑结构
设训练样本集为X=[X1X2…XN]T,其中每个样本Xk=[xk1xk2](k=1,2,…,N),Di=[di1di2](i=1,2,…,M)为隐层第i个径向基函数中心。RBF函数为高斯函数,训练样本Xk输入网络后,隐层第i个节点输出为:
i=1,2,…,M
(9)
其中,δi为RBF函数第i个节点方差。
网络输出节点y值是隐层输出与连接权值的点积,即
(10)
RBF神经网络需要调整的参数有RBF函数中心、方差和连接权值,本文采用梯度下降算法[11]。定义目标函数E为:
(11)
其中,N为训练样本数;ysk为期望输出值;yk为输入第k个样本时的网络输出。
为使目标最小化,各参数调整量与目标函数负梯度成正比,比例系数为η,经整理后,各参数的调整值计算式为:
(12)
(13)
(14)
其中,Δdj为RBF函数中心变化量;Δδj为RBF函数方差变化量;Δwj为连接权值变化量。
4 电动汽车ABS控制策略
4.1 电动汽车ABS控制系统设计
电动汽车ABS通过调整制动力矩使车辆实际滑移率保持在最优滑移率处。模糊控制鲁棒性强、反应迅速,但可能存在静态误差,控制精度不足,因此本文设计一种运用模糊控制与预测控制相结合的ABS控制策略,具体设计如下所述。
(1) 模糊控制器设计。模糊控制器的2个输入参数分别是轮胎滑移率误差e和误差变化率ec,输出参数是制动力矩的调整参数u[13],有
e=λ-λopt
(15)
(16)
ΔT=Ku
(17)
其中,K为比例系数;ΔT为制动力矩的变化量。
根据经验及参考实验数据,取2个输入参数的基本论域分别为[-0.15,0.15]、[-20,20],输出参数的基本论域为[-1,1],量化论域均取为[-6,6],且均划分为7个模糊子集,对应负大(NL)、负中(NM)、负小(NS)、零(ZE)、正小(PS)、正中(PM)及正大(PL)。
模糊控制器输入及输出参数的隶属度函数如图5所示。

图5 各参数隶属度函数
根据经验及仿真结果制定相应的模糊推理规则,见表3所列。
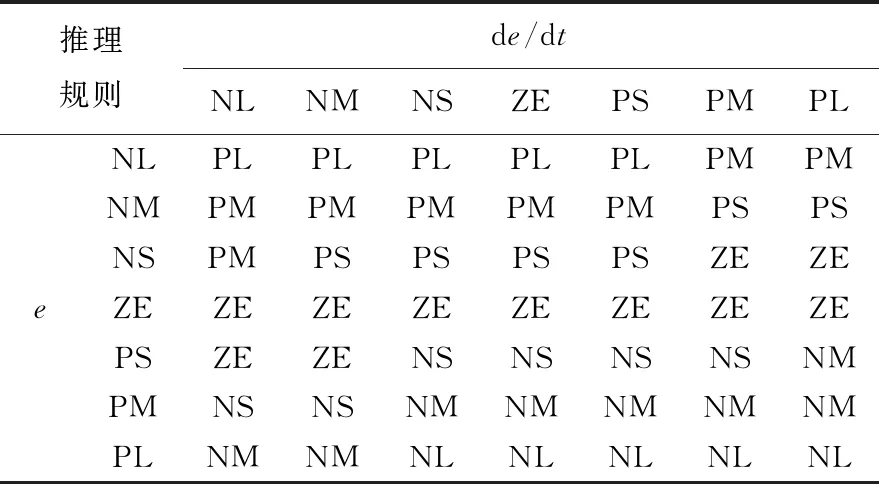
表3 模糊控制推理规则
(2) 预测控制理论。采用基于阶跃响应的动态矩阵控制[14],并用有限集合近似描述对象的动态信息,集合参数构成动态矩阵的模型参数。其中a=[a1a2…aS]T,表示模型向量,S为建模时域。设在k时刻控制有一增量Δu(k)时,可以计算出在其作用下未来时刻的输出值为:
y1(k+i|k)=y0(k+i|k)+aiΔu(k),
i=1,…,S
(18)
由(18)式导出性能指标与Δu的向量关系为:
yP1(k)=yP0(k)+AΔu(k)
(19)
其中,A=[a1a2…aP]T;yP0(k)为k时刻未加Δu(k)时的初始预测值;yP1(k)为k时刻在Δu(k)作用下的模型预测值。yP0(k)、yP1(k)可表示为:
yP0(k)=
[y0(k+1|k)y0(k+2|k) …y0(k+P|k)]T,
yP1(k)=
[y1(k+1|k)y1(k+2|k) …y1(k+P|k)]T。
采用二维模糊预测控制器,控制器在k时刻的输入是过程的控制参数e、ec,输出是控制律的修正量。
4.2 电动汽车ABS制动力矩分配策略
为保证车辆获得最佳的制动性能,根据I曲线和欧洲经济委员会(Economic Commission of Europe,ECE)法规调整前、后轴的制动力矩[15-16],同时考虑制动能量回收,设计了前置前驱电动汽车制动力矩分配策略,如图6所示。其中,vmin为电动机回收制动能量的最低车速;vABS为ABS起作用的最低车速;Tmax为电动机此时所能提供的最大制动力矩;TfABS、TrABS分别为前、后轴ABS制动力矩;z为制动强度;λ1、λ2为前、后轴轮胎的实际滑移率。

图6 制动力矩分配策略
5 基于CarSim/Simulink建模及验证
5.1 实例样车及其技术参数
以某前置前驱电动汽车为实例样车,其整车及零部件技术参数见表4所列。

表4 参考车辆主要参数
5.2 仿真模型的建立
通过CarSim仿真平台搭建整车动力学模型,在Matlab/Simulink中搭建控制策略模型,两者联合仿真。CarSim作为专业化的车辆仿真平台,其整车模型具有相当高的准确性,通过I/O接口可实现CarSim与Simulink的信息互通,在扩展CarSim应用的同时提高了Simulink的仿真准确度。仿真车辆主要参数见表4,搭建的仿真模型如图7所示。该模型主要包括驾驶员模型、制动控制策略模型、制动系统执行机构模型及整车动力学模型等。

图7 电动汽车ABS联合仿真模型
5.3 电动汽车ABS仿真验证及结果分析
5.3.1 对接路面制动仿真
在CarSim仿真平台设置制动初速度为100 km/h,平直路面附着系数为0.3,当制动距离达到30 m时,进入附着系数为0.6的对接路面,初始SOC置为0.6,车辆质量为1 380 kg,vmin、vABS均置为10 km/h。
制动过程中,驾驶员用力踩下制动踏板,控制系统根据制动踏板位移信号增加制动轮缸液压力,制动力矩迅速增大,滑移率随之增加,这有利于路面识别模块快速识别路面真实最优滑移率。采用模糊控制时的仿真结果如图8所示。
由图8可知:
(1) 开始制动后车速减小,0.065 s时识别模块识别出路面最优滑移率为0.096,轮胎实际滑移率大于该值时启动ABS;制动距离达到30 m时车辆进入对接路面,RBF网络识别出此时最优滑移率为0.131,如图8b所示;通过ABS调整制动力矩,将滑移率控制在新的最优滑移率处,如图8e、图8f所示;此时车速降低更快,如图8a所示。
(2) 当车速低于10 km/h时,关闭ABS,之后制动力矩直接由驾驶员控制,直至车速减为0,如图8c、图8d所示。
(3) ABS作用期间,再生制动系统持续工作,动力电池SOC值有所增加,当车速降至10 km/h之后,电机不再回收能量,SOC值保持不变,如图8g所示。经计算,电机回收能量约占总制动能量的14.8%。
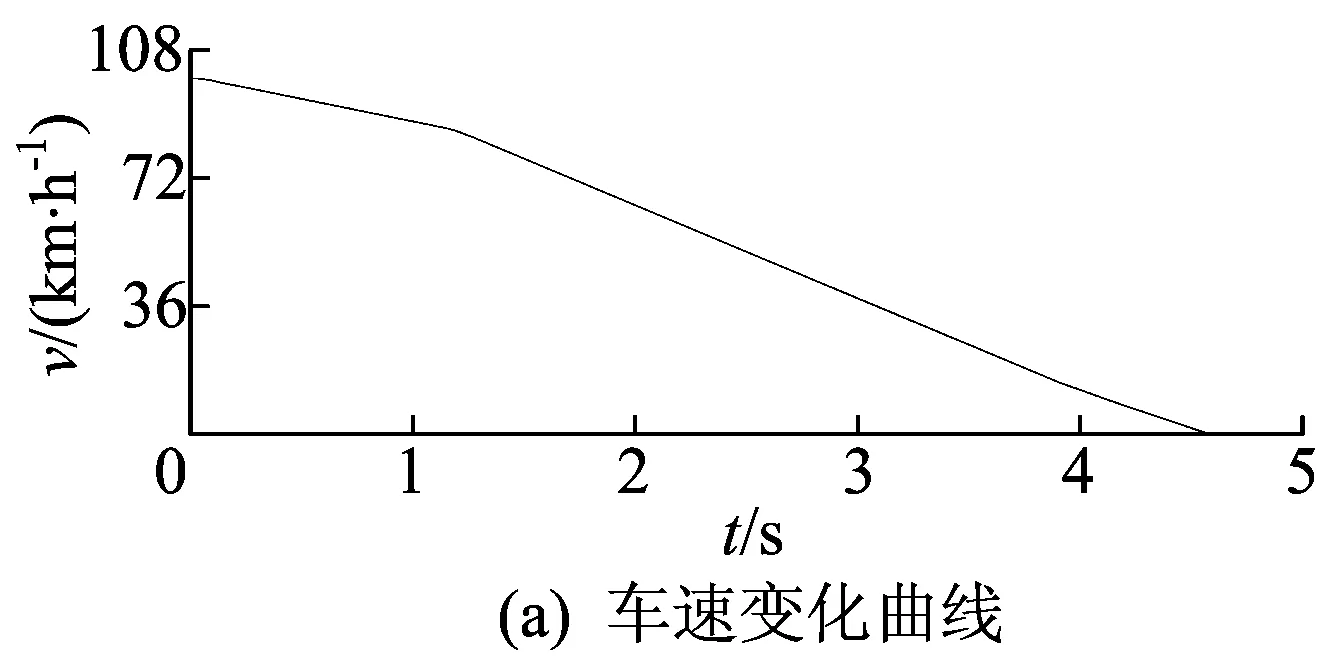
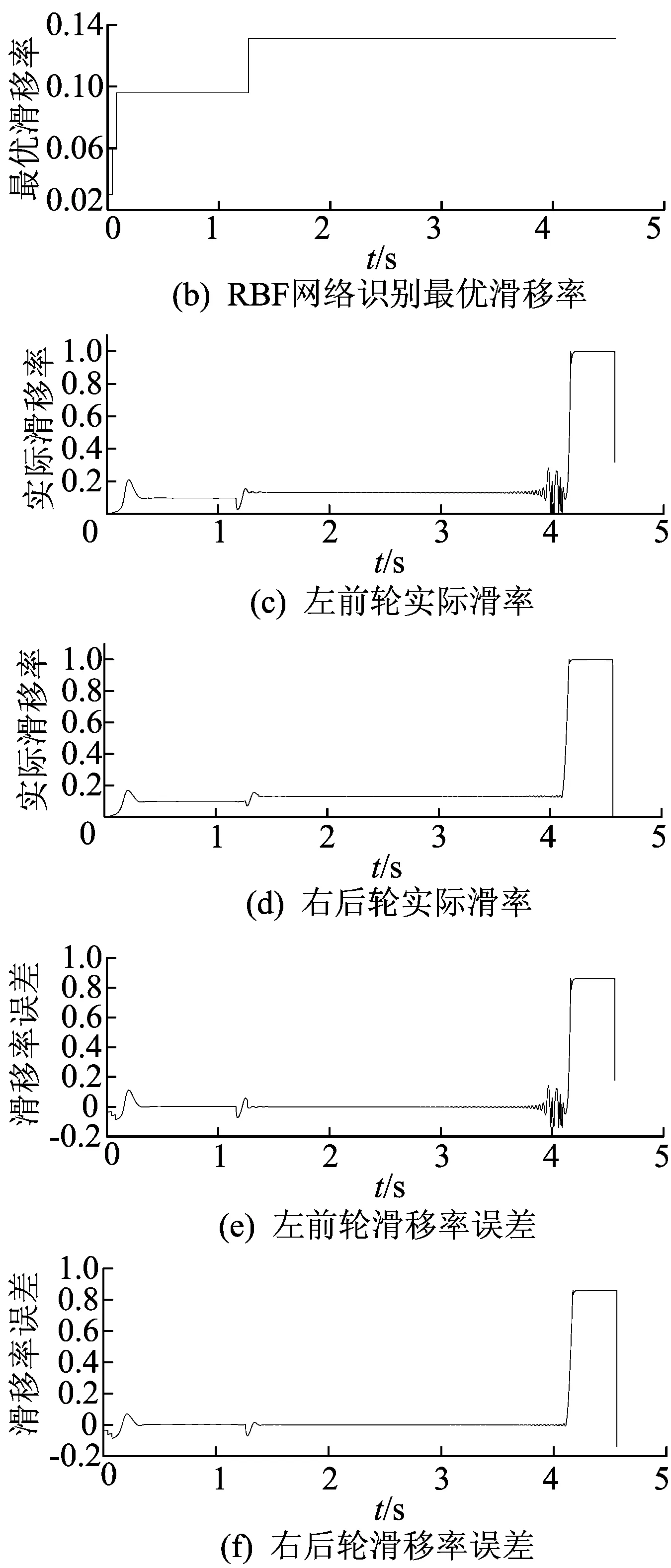
图8 模糊控制仿真结果
5.3.2 模糊预测控制
由于前轴驱动电机进行制动能量回收,车速较小时电机再生制动力矩变化较大,使得在模糊控制作用下前轴轮胎实际滑移率出现较明显的波动。为解决该问题并进一步提高制动性能,采用模糊预测控制设计制动策略,仿真结果如图9所示。
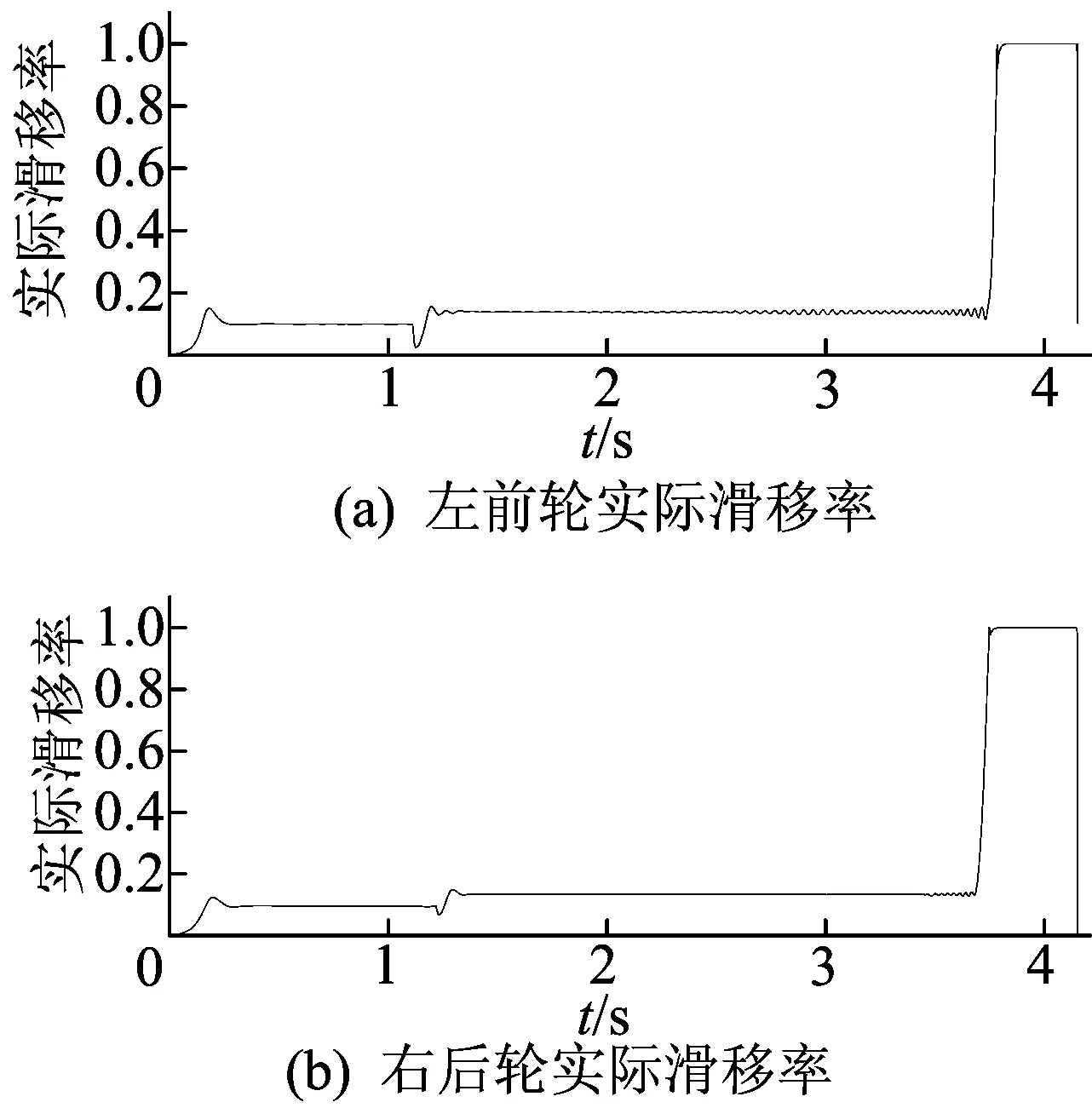

图9 模糊预测控制仿真结果
制动距离仿真结果的对比如图10所示,具体数据见表5所列。
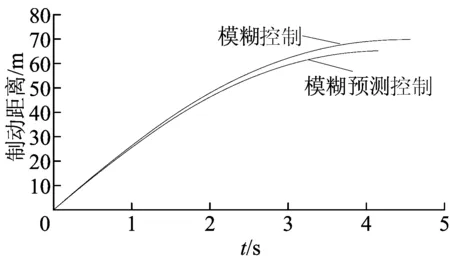
图10 制动距离变化曲线

表5 仿真结果的对比
由图9和表5可知,采用模糊预测控制时,实际滑移率稳定维持在最优滑移率处,制动距离相对模糊控制时减小6.57%,制动安全性更高,控制效果更好。另外,经计算电机回收能量约占总制动能量的18.7%,相比模糊控制,其制动能量回收提高3.9%。
6 结 论
本文设计了一种基于RBF神经网络路面识别的电动汽车ABS控制方法,通过模糊控制和预测控制联合作用调整制动力矩,将轮胎实际滑移率控制在最优滑移率处,同时制定了制动力矩分配策略,并搭建了CarSim与Simulink联合仿真模型验证控制策略可行性。仿真结果表明,本文路面识别方法准确有效,ABS控制效果良好,制动力矩分配合理,制动距离相对于模糊控制时减小了6.57%、制动能量回收提高了3.9%。

