永磁型磁流变阻尼器力学性能有限元分析

陈怡君, 周 律, 杨丽红, 涂田刚

(1.上海理工大学 机械工程学院,上海 200093; 2.上海材料研究所,上海 200437)

磁流变液(magnetorheological fluid,MRF)是一种新型的智能材料,由母液、磁性粒子及抗沉降添加剂组成,具有优良的物理及流变特性,在外加磁场的作用下,可实现其固态和液态之间毫秒级内连续的快速转变。以MRF作为填充材料的磁流变阻尼器(magnetorheological damper,MRD)通过改变线圈电流的方式对振动进行主动控制,使整个振动系统具有优越的隔振和减振性能,广泛应用于车辆、航空和机械加工等领域的减振、制振中。但是这种电磁调节式的MRD对供电系统的可靠性有很高要求,尤其是在电力供应中断时将导致整个阻尼器失效,易造成重大事故。因此,人们开发了阻尼可调的永磁型MRD,其既可以根据现场要求调节阻尼大小,又具有比传统MRD更高的可靠性和稳定性。

目前,MRF已被成功应用于Cadillac系列轿车磁流变悬架控制系统、磁流变风扇离合器、火神系列火炮、土木工程、飞行器、直升机、微机械、智能抛光技术等民用和军用领域[1],如文献[2]研究了MRF在旋转密封中的应用。文献[3]基于电磁式振动能量回收技术构建了具有自供电特性的MRD斜拉索减振系统,模型斜拉索减振试验结果表明,相对于外供电MRD最优被动控制,除对斜拉索第1阶模态的减振效果基本相当外,自供电MRD对斜拉索高阶模态的减振效果更优。文献[4-6]将阻尼通道处的磁通密度假设成一个定值,进而认为整个活塞阻尼通道处MRF的剪切屈服强度相同。但已有的文献多着重研究常规外接电源的剪切阀式MRD,而对永磁型MRD的仿真模拟鲜有报道。由于永磁型MRD本身结构的特点,在整个阻尼通道各处的磁场强度差值很大,阻尼通道的等效长度很难确定,现有的计算方法不能很好地描述永磁型MRD的动力特性。

本文基于COMSOL软件,以Bingham模型描述MRF的流变特性,将流体剪切屈服强度与磁场强度相关联,借此描述因磁场强度不均匀性导致的通道各处剪切屈服强度的不同;在此基础上建立永磁型MRD的有限元模型,分析不同挡位下阻尼器的耗能情况,并与试验值进行对比。

1 阻尼器结构及其有限元模型

1.1 阻尼器结构

永磁型MRD模型结构如图1所示,其材料参数见表1所列。用永磁铁代替线圈作为磁场发生装置,由于材料存在磁阻,磁力线穿过材料时将产生磁损耗以及漏磁现象,导致阻尼通道处流体磁场强度不均匀，很难计算出活塞工作区域的等效宽度。

图1 永磁型MRD模型结构

表1 磁场模型材料参数

1.2 MRF流变本构方程

MRF在稳态下可以看做Bingham流体,其本构方程[7-8]可以表示为:

(1)

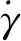
MRF的等效黏度[9]可表示为:

(2)

COMSOL计算黏性不可压缩流体的本质是求解Navier-Stokes方程,即

(3)

1.3 磁流耦合场有限元模型

本文MRF型号为宁波杉工的MRF-J01,其特性参数零场黏度为0.47 Pa·s，剪切屈服强度为：

τy(B)=0.354 0B4-0.671 2B3+

0.371 5B2+0.014 7B。

在流场分析中,将其磁场的初始值设置为之前磁场有限元模型的求解值，如图2所示。通过设置流体黏度对磁场强度的相关函数,将流体各处的磁场强度分布转变成流体在各处的黏度分布[10]。因为阻尼通道间隙相对于通道长度极小,所以将流场设置为层流,壁面边界条件为无滑移。

图2 磁流耦合设置

将所有与缸壁接触部分的边界速度在r方向 和z方向上均置为0,如图3所示,运用动网格的方法将所有与活塞和活塞杆接触部分的边界速度在r方向上置为0,在z方向置为v=62.8×sin(6.28t) mm/s。

图3 动网格设置

2 仿真结果与试验测试

2.1 仿真结果

永磁型MRD在0挡、3挡下的磁场分布和初始屈服强度分布分别如图4、图5所示。

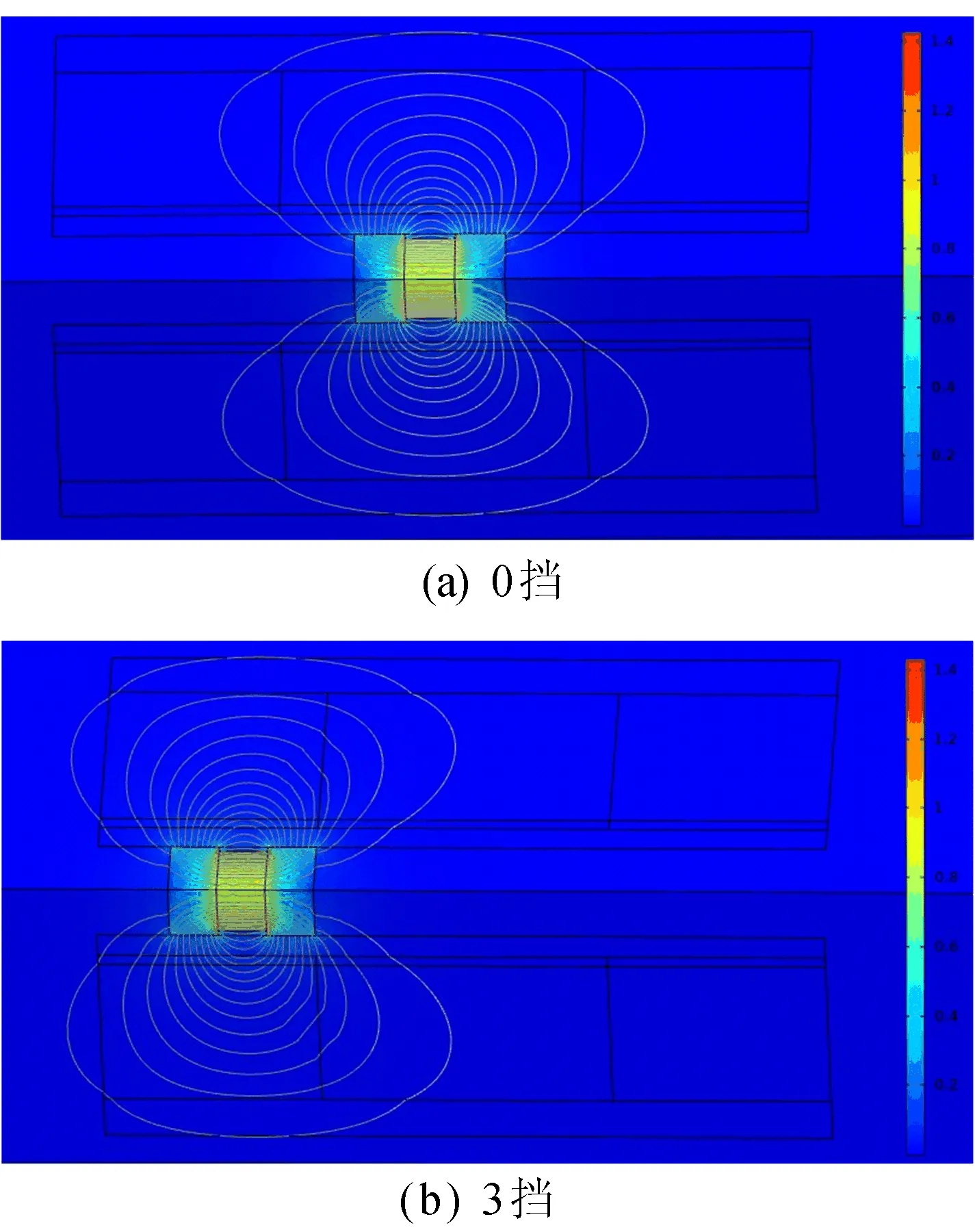
图4 0挡、3挡下的永磁型MRD内磁场分布

图5 0挡、3挡下的初始流体屈服强度分布

在同一坐标下的MRF初始黏度与磁通密度成正相关,离导磁块越近其黏度越高,相应的屈服应力也越高,对阻尼器阻尼的贡献也越大。从图4可以看出,随着挡位升高,磁铁向阻尼通道中心区域外侧移动,阻尼通道的工作区域长度随之变短;当挡位调整至3挡时,磁铁离阻尼通道中心最远,此时工作区域长度最短,在此情况下也最难确定等效的工作区长度。

有限元计算出的永磁型MRD滞回曲线如图6所示。

由图6可知,在3挡下阻尼通道处屈服强度很小,在库仑力和黏滞力组成的阻尼力中,黏滞力占主要部分,大小与MRF的零场黏度成正相关;而在0挡下库仑力占主要成分,大小与屈服强度成正相关。因此,永磁型的MRD阻尼力可调倍数主要与流体的屈服强度成正相关,与零场黏度成负相关。

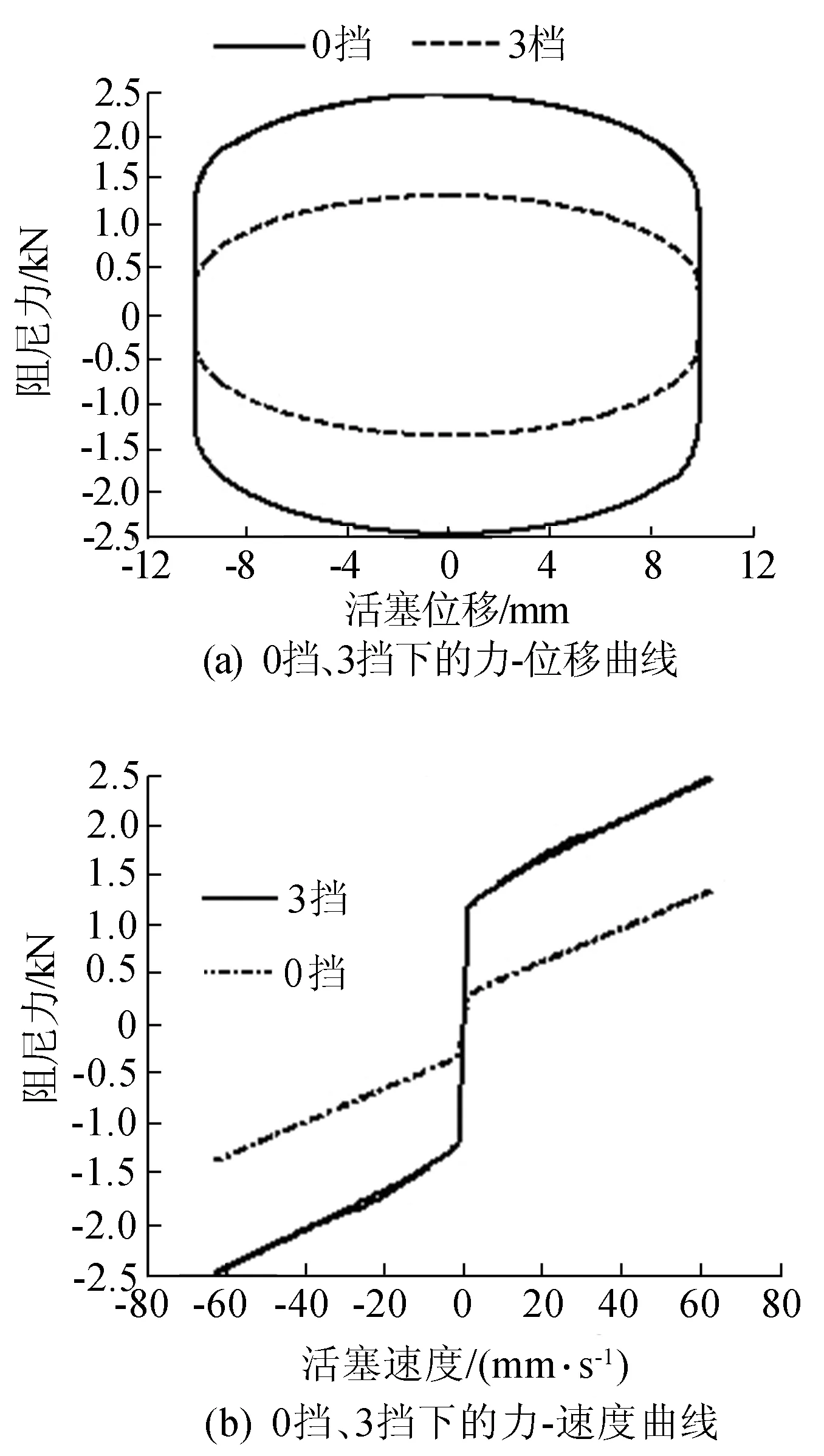
图6 阻尼力有限元计算值

由于需要考虑阻尼器强度因素,其活塞轴外壁不能做得很薄,导致流体区域的磁场强度较低,其屈服强度也较低,在0挡和3挡模式下工作区域内的磁场强度之比相比于外接电流的传统MRD小很多,因此在满足最大阻尼力的前提下，永磁型MRD选择低零场黏度的MRF有助于提高阻尼器的可调倍数。

2.2 试验测试

试验平台如图7所示。

图7 试验平台

平台加载由电液伺服机驱动,测试系统为自建的NI系统,采用华东仪器有限公司的BLR1-700 kg压力传感器。接通电源后打开试验软件,启动伺服油泵将阻尼器拉至行程中点位置,并清零载荷后以频率为1 Hz、振幅为10 mm的正弦位移激励对阻尼器进行加载,取第2个周期的阻尼器力-速度曲线的试验值与有限元仿真值进行对比,结果如图8所示。

图8 永磁型MRD力-速度曲线

现有的描述MRF的流变模型主要有Bingham模型、Herschel-Bulkley模型和自定义PDE微分方程3种。其中Bingham模型形式简单易于程序化,但忽略了屈服前的黏弹性和高剪切率下存在的剪切稀化现象[11];自定义PDE微分方程不仅能描述MRF剪切稀化及屈服后的黏塑性,还能很好地描述其屈服前因黏弹性引起的滞后性,但是若将磁场因素耦合进PDE中，则会造成方程过于复杂、计算难度过大、无法收敛;同理,虽然Herschel-Bulkley模型能够描述剪切稀化现象,但同样存在着难收敛的问题。因此在仿真中采用Bingham模型描述MRF的流变特性,同时因为阻尼器在灌注MRF时存在气泡和未灌注满的情况,所以在低速阶段试验值与仿真值在速度上存在滞后叠加;在中高速阶段流体进入屈服后区,仿真值能够很好地拟合永磁型MRD的力-速度关系。

本文在对阻尼器力学性能仿真时没有考虑活塞轴与密封圈之间的摩擦反力,因此阻尼器的仿真值略小于试验值。

3 结 论

本文利用COMSOL软件对某永磁型MRD力学性能进行有限元分析,通过将流体黏度与磁场强度相关联,并利用求出的磁场强度推导出流体区域的黏度场,进而得到阻尼器的力学仿真特性,并与试验结果比较,表明该仿真方法在中、高速加载下是可行的。

利用磁流耦合方法仿真阻尼器的力学性能可以在计算阶段得到磁铁安装位置、加载速度、磁铁剩磁与输出阻尼力之间的关系,为永磁型MRD的设计研发提供了一种具有参考价值的数值方法。