Pythagorean模糊幂Bonferroni集成算子及其决策应用

骆丹丹，曾守桢 ，2

1.宁波大学 商学院，浙江 宁波 315211

2.复旦大学 管理学院，上海 200433

1 引言

Atanassov于1986年提出的直觉模糊集[1]，是对经典Zadeh模糊集[2]理论的重要拓展。相比模糊集只能用单一的隶属度刻画抽象概念的肯定程度，直觉模糊集增加了非隶属度来表示否定程度，从而更加细致全面地刻画客观世界的模糊性本质。由于直觉模糊集的隶属度和非隶属度之和必须满足小于等于1的条件，因此在一些实际应用问题中受到很多制约。为此，Yager对其进一步拓展提出了毕达哥拉斯模糊集[3]，将条件拓宽至允许隶属度和非隶属度之和大于1，而其平方和小于等于1，故其比模糊集、直觉模糊集具有更强的描述模糊现象的能力。

近年来，关于毕达哥拉斯模糊集的理论研究和应用探索得到许多学者的关注。其中，Akram等人[4]提出了一系列毕达哥拉斯Dombi模糊集成算子。Khan等[5]将优先集成算子拓展到毕达哥拉斯模糊环境中以解决属性和决策者间存在优先级关系的决策问题。刘卫锋等人[6]定义了毕达哥拉斯模糊的Hamacher运算方法；Wei[7]在毕达哥拉斯模糊环境下利用Hamacher运算和幂集成算子提出了一系列毕达哥拉斯模糊Hamacher幂集成算子。Verma等人[8]提出了一种基于三角相似性测度的毕达哥拉斯模糊多属性决策方法。曾守桢等[9]提出了一种基于混合加权测度的TOPSIS决策方法来解决决策信息为毕达哥拉斯模糊数的多属性决策问题。Fei等人[10]定义了基于OWA算子的软似然函数以识别决策者的主观偏好。Jin等[11]将毕达哥拉斯模糊集与语言术语集结合，定义了毕达哥拉斯模糊语言集。刘卫锋等[12]将毕达哥拉斯模糊集与犹豫集结合，定义了毕达哥拉斯模糊犹豫模糊集；Garg[13]进一步提出了毕达哥拉斯犹豫模糊混合集成算子。

上述有关毕达哥拉斯模糊信息的集成方法与应用都是在属性间相互独立的情况下提出的。实际决策中，不同属性间可能存在不同程度的关联性，或互补、冗余、偏好关系等。由Bonferroni[14]于1950年提出的Bonferroni平均（BM）算子是一种均值类型的集成算子，它能有效地捕获输入变量间的相互关联情况，将多个输入变量集结成一个变量，是一种有界的集成算子。近年来BM算子得到广大研究者的关注并被拓展应用到不同模糊决策问题中[15-19]。另一方面，幂平均（PA）算子也是一种能有效考虑数据信息之间关联性的集成算子[20]，其通过考虑输入数据之间的支撑度关系计算属性权重，可以有效减少异常数据对决策结果的影响，使得决策信息的处理过程更加客观公正，因而受到很多学者的关注[21-26]。为了综合利用Bonferroni平均（BM）算子和幂均（PA）算子的优点，He等[27]将PA算子与BM算子相结合，提出幂Bonferroni平均（PBM）算子。之后，人们将PBM 算子拓展到不同模糊环境中，包括犹豫模糊集[27]、直觉模糊集[28-29]、区间直觉模糊集[30]和语言直觉模糊集[31]；进一步的，Khan等[32]基于Dombi运算，将PBM算子拓展到区间中智环境中以处理区间中智信息的多属性决策问题。然而，到目前为止，还没有关于如何利用PBM算子集成毕达哥拉斯模糊数的研究。因此，为了丰富毕达哥拉斯模糊集的集成方法和拓展PBM算子的应用领域，本文将研究基于PBM算子的毕达哥拉斯模糊集成方法，提出两种新的毕达哥拉斯模糊信息集成新算子，即毕达哥拉斯模糊幂Bonferroni平均算子和毕达哥拉斯模糊加权幂Bonferroni平均算子，并在此基础上，给出一种新的毕达哥拉斯模糊多属性决策方法。

2 预备知识

定义1[3]给定论域X上的毕达哥拉斯模糊集P为：

其中，μP(x):X→[0,1] 和νP(x):X→[0,1]分别代表P的隶属函数和非隶属函数，且∀x∈X有1，且x属于P的犹豫度为为计算方便，称α=μα,να为毕达哥拉斯模糊数（PFN）[33]。

定义2[33]设达哥拉斯模糊数，定义：

关于毕达哥拉斯模糊数更多的运算规则等知识，可参见文献[33-34]。

定义3[35]设为两个毕达哥拉斯模糊数，它们之间的支撑度定义为：

为毕达哥拉斯模糊数的距离，παi(i=1,2) 为αi(i=1,2)的犹豫度。

定义4[20]设为实数，则称：

为幂平均（PA）算子。其中(i=1,2,…,n),Sup(xi,xj)表示xi和xj之间的支撑度，并满足下列条件：

定义5[14]设p≥0,q≥0，且p与q不同时为0，xi(i=1,2,…,n)为一组非负实数，则称：

为Bonferroni平均（BM）算子。

定义6[27]设xi(i=1,2,…,n)为一组非负实数，且p,q≥0，则称：

为幂Bonferroni平均（PBM）算子。

3 毕达哥拉斯模糊幂Bonferroni集成算子

考虑到PA算子能根据属性之间的支持关系确定属性权重，从而减少有偏决策者给出异常偏好值对决策结果的影响，而BM算子则能充分考虑属性间的相互关联关系，因此，本章根据PA算子和BM算子的特性将两者结合起来，并将其扩展到毕达哥拉斯模糊环境中，提出基于毕达哥拉斯模糊数的PBM算子。

定义7设p与q为不同时为0的两个非负实数，αi=μi,νi(i=1,2,…,n)为一组毕达哥拉斯模糊数，若：

称PFPBMp,q为毕达哥拉斯模糊幂Bonferroni平均（PFPBM）算子。其中，T(αi)=Sup(αi,αj)(i=1,2,…,n)，Sup(αi,αj)表示毕达哥拉斯模糊数αi和αj之间的支撑度，并满足定义4中的条件。

基于毕达哥拉斯模糊数之间的运算法则，可得定理1。

定理1设p与q为不同时为0的两个非负实数，αi=μi,νi(i=1,2,…,n)为一组毕达哥拉斯模糊数，则经过PFPBM算子得到的集结值仍然是毕达哥拉斯模糊数，且

显然有ῶk≥1。则式（7）和式（8）可分别简化为式（10）和式（11）：

下面，证明定理1，即证明公式（11）成立。

证明 基于毕达哥拉斯模糊数之间的运算法则，可以得到：

成立，即PFPBMp,q(α1,α2,…,αn)仍然是一个毕达哥拉斯模糊数。

综上，定理1得证。

PFPBM算子还具有幂等性、置换不变性、有界性等优良性质。

性质1（幂等性）设αi=μi,νi(i=1,2,…,n)为一组毕达哥拉斯模糊数，若α1=α2=…=αn=α，则：

性质2（置换不变性）设αi=μi,νi(i=1,2,…,n)为一组毕达哥拉斯模糊数，若(α′1,α′2,…,α′n)为(α1,α2,…,αn)的任意置换，则：

由定义7和定理1可以看出，PFPBMp,q(α1,α2,…,αn)算子只考虑了基于幂算子的权向量和待集成毕达哥拉斯模糊数之间的相关性，并没有考虑数据本身的重要性，即该集成算子是在集结变量重要程度相等的情形下定义的。然而，在许多实际决策过程中，不同属性的重要程度可能不同，因此它们的权重也不相等。为了融入指标权重的重要性，接下来将定义毕达哥拉斯模糊幂加权Bonferroni平均（PFPWBM）算子。

定义8设p与q为不同时为0的两个非负实数，为一组毕达哥拉斯模糊数，权重向量

称PFWPBM为毕达哥拉斯模糊加权幂Bonferroni平均（PFWPBM）算子。其中，(i=1,2,…,n)，Sup(αi,αj)表示毕达哥拉斯模糊数αi和αj之间的支撑度，并满足定义4中的条件。

定理2设p与q为不同时为0的两个非负实数，为一组毕达哥拉斯模糊数。经过PFWPBM算子得到的集结值仍然是毕达哥拉斯模糊数，且

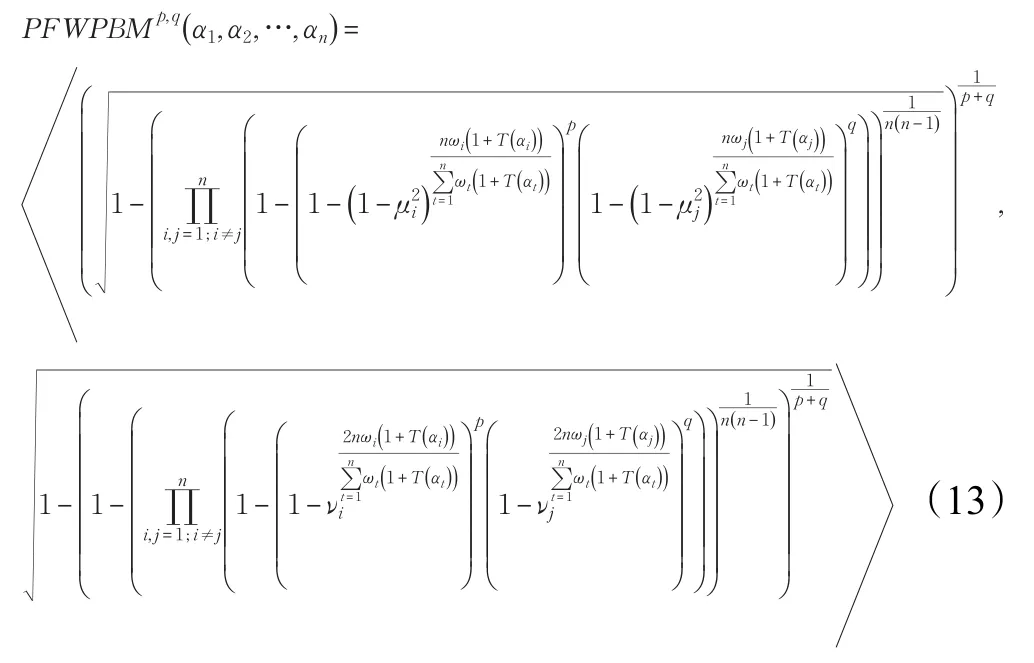
证明过程类似定理1，限于篇幅，此处略去。

与PFPBM算子类似，PFWPBM算子也具有置换不变性和有界性。

下面将讨论关于PFWPBM算子的几种特殊情形，可以发现，现有很多算子是本文所提PFWPBM算子的特例。

此时PFWPBM算子退化为毕达哥拉斯模糊加权Bonferroni平均（WPFBM）算子[17]，该算子不具备幂平均算子的优点。

此时PFWPBM算子退化为PFPBM算子，显然PFPBM算子是PFWPBM算子的特殊情况。

4 基于PFWPBM算子的多属性决策方法

从以上分析可知，PFWPBM算子综合考虑PA算子和BM算子在实际决策问题中的优点，既能有效减少异常数据对决策结果的影响，又能充分考虑属性间的相关性，基于此，下面提出一种基于PFWPBM算子的多属性决策方法。

对于毕达哥拉斯模糊多属性决策问题，设有n个备选方案A={A1,A2,…,An}，m个决策属性C={C1,C2,…,Cm} ，对应决策属性的权重向量为 ω=(ω1,ω2,…,ωm)T。其中，ωi∈[0,1]，=1。假设邀请专家提供毕达哥拉斯模糊评价信息，得到毕达哥拉斯模糊决策矩阵M=(αij)n×m，αij=μij,νij。其中，μij和νij分别表示备选方案Ai关于决策属性Cj的隶属度值和非隶属度值。基于PFWPBM算子的多属性决策方法的步骤如下：

步骤1根据实际情形，建立毕达哥拉斯模糊决策矩阵 M=(αij)n×m，并利用文献[36]给出的规范化方法，将M=(αij)转化为规范矩阵n×m。

步骤2计算输入变量间的支撑度。

其中，k,j=1,2,…,m；l=1,2,…,n。

步骤3根据决策属性对应的的权重向量计算毕达哥拉斯模糊数所对应的支撑度T()，进而获取变量的支撑度指数ξlk。

其中，k=1,2,…,m；l=1,2,…,n。

步骤4利用定义8中的PFWPBM算子对各个备选方案Ai(i=1,2,…,n)所对应的属性值1,2,…,m进行集结，得到备选方案Ai(i=1,2,…,n)的综合属性值),…,n。

步骤5计算综合属性值αi(i=1,2,…,n)的得分值，在属性得分值相等的情形下计算其精确值。依据αi(i=1,2,…,n)的优先级关系对备选方案Ai(i=1,2,…,n)进行排序，进而选择最优方案。

5 实例分析

本章考虑将上文研究得到的PFWPBM算子和决策模型应用到国内航空公司的服务质量评价中，以验证本文所提方法的有效性和可行性。

例现评价国内4家航空公司A={A1,A2,A3,A4}的服务质量[33]，计划从4个方面（属性）对这些公司进行评价，分别是定售票服务(c1)；登机程序(c2)；客舱服务(c3)和公司响应性(c4)，其对应的属性权重为ω=(0.15,0.25,0.35,0.25)T。假设专家提供的毕达哥拉斯模糊决策矩阵M=(αij)4×4,αij=μij,νij，如表1所示。试根据专家提供的决策矩阵，评价出服务质量最好的航空公司。

表1 毕达哥拉斯模糊决策矩阵

下面将用本文提出的决策方法，评价这4家国内航空公司的服务质量。

步骤1决策矩阵的规范化处理。由于所有属性都是效益型属性，因此不需要对上述决策矩阵进行规范化处理。

步骤2计算各个属性之间的支撑度，进而给出支撑度矩阵，得到：

步骤3计算变量和余下变量整体间的支撑度矩阵T()4×4，以及变量的支撑度指数矩阵ξ，得到：

步骤4利用PFWPBM集结算子对备选方案的综合属性值进行集结。为方便计算，这里选取参数p=1,q=1，计算得：

步骤5计算综合属性值αi,i=1,2,3,4的得分值S(αi)和精确值H(αi)(i=1,2,3,4)（如有必要）。

然后根据αi,i=1,2,3,4的得分值，得到各个备选方案的优先级关系为：

因此4家国内航空公司中，服务质量最高的是A4。

以上分析是在参数p=1,q=1情形下计算得到的。不失一般性，下面将讨论在不同参数取值下，最佳备选方案的变化情况，基于PFWPBM的计算结果如表2所示，相应的方案得分和排序如表3所示。

由表2和表3可知，随着参数p,q取值的变化，各个备选方案的综合属性值以及相应的得分值都发生了变化，最优备选方案（即4家国内航空公司中服务质量最高的）也相应地出现了改变，即由A4变为A2。进一步研究发现，备选方案的综合得分值将随着参数p,q取值的增大。因此，在决策过程中，决策者可以根据自身的风险偏好选择适当的参数p,q。若参数p,q取不同值，可类似分析。

为了更好地体现本文所提方法的优越性，下面进一步与现有方法进行比较分析，选取了文献[3]中的PFWA算子、文献[26]中的PFPWA算子、文献[17]中的WPFBM算子（为便于计算，集成算子中的参数统一取值1），对比结果如表4所示。

表2 PFWPBM集成算子的集成结果(p=q)

表3 PFWPBM集成算子的排序结果

由以上集成结果可知，本文与文献[26]中的PFPWA算子的最优备选方案相同，同为A4，而文献[3]中的PFWA算子和文献[17]中的WPFBM算子的最优备选方案同为A2。进一步的，发现各个方法的得分值以及排序结果也略有差异。导致上述差异的主要因素是以上几种模型算子均采用了不同的信息集成方法，且均基于算术平均的思想，但算子在集结过程中的侧重点不同。文献[3]中的PFWA算子主要是针对属性间相互独立的情况，没有考虑属性间可能存在的相互关系。而文献[17]中的WPFBM算子没有考虑数据信息之间的关联关系。本文给出的PFWPBM算子是结合PFPWA算子和WPFBM算子的优点，不仅考虑了属性间可能存在的相互关系，还反映了数据间的整体均衡性，从而避免有偏决策者给出异常偏好值（即原始数据中过大或过小的值）影响决策结果，使得决策更加公正客观。同时，新算子带有参数p,q，使得决策者可根据自身风险偏好灵活选取参数值，且调节系数n的增加，使得新算子在信息集成过程中更为稳健，较好地保留了算术平均算子本身的特性。

表4 对比分析结果

6 结束语

针对毕达哥拉斯模糊多属性决策问题，本文提出了两种新的毕达哥拉斯模糊集成方法，即毕达哥拉斯模糊幂Bonferroni平均算子和毕达哥拉斯模糊加权幂Bonferroni平均算子。新算子结合了幂均算子和Bonferroni算子的优良特点。不仅考虑了数据信息之间的整体均衡性，还考虑了属性之间可能存在的相互关联关系。进一步的，还探讨了新算子的一些优良性质和特殊情况。在此基础上，给出了基于毕达哥拉斯模糊加权幂Bonferroni平均（PFWPBM）算子的多属性决策方法以及详细步骤，并从实例和比较分析两方面验证所提方法的有效性和可行性。本文所提的决策方法也可以进一步应用到诸如供应商选择评价、产品方案选择评价、人力资源部门人才引进的推荐等领域中，具有一定的理论和应用价值。