向量化友好的循环分块因子选择算法

柴晓菲，刘 松，屈 彬，王 倩，伍卫国

西安交通大学 电子与信息工程学部，西安 710049

1 引言

在许多计算密集型应用程序中，特别是科学和工程计算应用程序，嵌套循环会耗费大部分的运行时间，成为亟待解决的程序热点[1]。循环分块[2-7]是一种应用广泛的循环优化技术，通过仿射变换对程序的嵌套循环部分进行代码转换，一方面增强程序的数据局部性，降低cache失效率；另一方面开发循环代码的粗粒度并行性，充分利用多核处理器的计算性能。分块后的循环迭代根据分块因子大小重置访存顺序，从而减小数据重用距离。因此，分块因子大小的选择对循环分块代码的性能有着重要的影响。近年来，随着SIMD扩展部件在微处理器和协处理器中的发展，向量寄存器的位数逐渐增加，使得自动向量化技术在开发嵌套循环的细粒度并行性方面得到有效提高[8-10]。但是，循环分块的分块因子大小不仅影响程序的局部性，也影响程序的自动向量化收益。因此，如何选择合适的分块因子，在保持程序访存局部性的同时充分利用向量化收益，对程序性能的提高具有积极的意义。

早期比较成熟的循环分块因子选择算法（Tile Size Selection，TSS）主要以改善程序局部性和开发程序粗粒度并行性为优化目标，而近年来提出的TSS算法不仅考虑了以上目标，还将开发程序的细粒度并行性作为一个优化目标。Feld等人[11]通过限定可向量化循环层的分块因子为向量因子（即向量寄存器可存放的最大操作数数目）的倍数关系来避免非对齐数据访问，并通过分析程序的内存访问模式，以最大化利用L1级cache为目标来确定最外层循环的分块因子。Mehta等人[12]通过对建立的TSS模型进行分析，指出在某些嵌套循环中，循环分块与向量化存在相互制约的关系，即循环分块会对循环迭代进行分割而向量化则需要较长的循环迭代，因此对可向量化循环层不进行分块处理。此后，Mehta等人[13]针对访存数组规模较大的嵌套循环，提出了一种改进的TTS模型，以充分利用微处理器的数据预取功能。虽然以上这些算法考虑了分块因子对向量化的影响，但是并没有量化地分析不同分块因子对向量化收益的影响。此外，以上算法研究的对象是访存数组大小为向量因子整数倍的嵌套循环，对于不满足该条件的嵌套循环（称为病态规模循环），以上研究并未给出详细分析。

为了解决这些问题，本文提出了一种针对可向量化嵌套循环的分块因子选择算法（VECtorization Tile Size Selection，VEC-TSS），能够使分块后的程序同时充分地利用编译器的自动向量化技术和处理器的多级cache架构资源。该算法的创新点主要有：（1）量化分析了循环分块后程序的向量化收益；（2）详细分析了病态规模问题的分块因子选择过程。

2 VEC-TSS算法

通常情况下，当嵌套循环的最内层循环没有跨迭代依赖时，主流编译器会对该层循环进行自动向量化处理。本文提出的VEC-TSS算法仅适用于具有可向量化循环层的嵌套循环。对于正常问题规模的嵌套循环，只要分块因子的大小是向量因子的整数倍，就可以避免地址非对齐数据访问，不会影响向量化收益。但是对于病态规模问题，任何一种分块因子都会导致向量化时的地址非对齐数据访问。当嵌套循环为病态规模问题时，相较于其他TSS算法，VEC-TSS算法更能有效地降低向量化收益受分块因子大小的影响。VEC-TSS算法分为两个部分：可向量化循环层的分块因子选择和其他循环层的分块因子选择。

2.1 可向量化循环层的分块因子选择

为了有利于编译器对嵌套循环进行自动向量化，可以借助代码转换工具（如PLuTo）将可向量化循环层置换到最内层，本节讨论可向量化循环层的分块因子选择，即嵌套循环的最内层循环的分块因子选择。

程序能够向量化的前提有两点：（1）访问地址连续的数据；（2）访问地址对齐的数据[14]。经过循环分块后的程序改变了循环边界，进而改变了向量寄存器访问数据的地址对齐性，但是并不会影响分块内访问数据的地址连续性，因此本文仅讨论循环分块对地址对齐性的影响。不同大小的分块因子产生的循环边界不同，使得分块后的嵌套循环中非对齐数据的数量也不相同。目前的主流处理器对存在地址非对齐数据访问的程序进行自动向量化时，会额外采用循环展开、循环剥离、数组填充等技术[15-16]，从而增加了开销，降低了向量化收益。为了便于接下来的分析，定义可向量化数据块为内存中连续的向量因子大小的数据，其第一个数据的地址对齐于向量寄存器；定义可向量化数据的数目（记为NUM_VEC）为所有可向量化数据块中的数据个数。可向量化数据越多，向量化收益也越大。为了获得最大化的向量收益，本文选择的可向量化循环层分块因子大小应使得循环体中所有可向量化数据的数目最大。

以图1为例进行说明，（a）和（b）分别表示矩阵乘法分块前后的核心代码。其中，分块因子为(I,J,K)，参与计算的数据类型为8 Byte的双精度浮点型。目标机器的向量寄存器大小为256位，则向量寄存器一次能够存取4个数据，要求存取的第一个数据的内存地址是32 Byte对齐的。假设数组的首内存地址为32 Byte对齐，当问题规模N=13时，数组C[i][j]在内存中的数据存储情况如图2所示。图中每一个方格代表数组的一个元素。以分块因子(I,J,K)对循环进行分块，则影响数组C[i][j]的分块因子是(I,J)，行分块因子是I，列分块因子是J。图2中相同颜色（灰度）的方格表示在相同的分块中。因为 j循环层可以向量化，此时可向量化循环层分块因子为J。

图1 分块前后矩阵乘法matmul的核心代码

图2 内存中数组C的数据布局（分块因子为6）

观察图2，数组的第一行C[0][:]分成三部分，位于三个块中。第一块中的C[0][0:5]首先被载入cache中参与计算，其中C[0][0:3]是可向量化数据，而C[0][4:5]大小不是向量寄存器大小，无法向量化，故记可向量化数据个数为4。第二块中的C[0][6:11]被载入cache中参与计算时，C[0][6]的内存地址非对齐，C[0][6:7]无法向量化，而C[0][8:11]可以向量化，故记可向量化数据个数为4。同理分析数组的其余行，最终得到当 J=6时，NUM_VEC=104。

为了使可向量化循环层的收益最大，要求该层的分块因子J对应的NUM_VEC最大。当数组大小为N时，遍历所有的分块因子 J(1≤J≤N)，并计算相应的NUM_VEC值，则可向量化循环层的最优分块因子Best_J的计算如公式（1）所示：

2.2 其他循环层的分块因子选择

本节将详细分析影响分块因子选择的另外两个重要因素——程序局部性和并行粒度，并由此建立候选分块因子的搜索空间，从中确定最优分块因子。

2.2.1 候选分块因子的搜索空间

（1）程序局部性

循环分块技术通过减小块内数据的重用距离，使得数据在下一次被访问时没有因为cache容量被替换出去而得到重用，从而带来局部性收益。因此本文以数据重用距离（Reuse Distance，RD）来度量程序局部性。RD指同一个数据在两次重用之间所访问的其他不同数据的个数。以图1（b）的代码为例，分块因子为(I,J,K)，对于数组B[k][j]来说，块内循环的最外层i每迭代一次，数组B才能得到重用。数组B的两次重用之间总共访问了数组A[i][k]的K个不同元素、数组C[i][j]的J个不同元素以及数组B[k][j]本身的K×J-1个不同元素，故数组B的重用距离RDB=K+J+(K×J-1)。推广到一般情况，下面给出数据重用距离RD的计算公式。

对于一个n层嵌套循环，分块因子为T=(T1,T2,…,Tn)，其中Ti代表第i层循环的分块因子。循环语句S访问的数组有A1,A2,…,Am，则此嵌套循环中的数据访问矩阵ACC的结构如公式（2）所示：

其中ai,j代表数组Ai在第 j层循环上的数据访问情况，如公式（3）所示：

ai,j=1表示数组Ai在第 j层循环上具有数据重用。标记重用循环层的向量C=(C1,C2,…,Cm)表示访问矩阵ACC每一行中第一次出现1的列号，代表的含义是数组Ai在第Ci层循环上具有数据重用。则数组Ai的重用距离和循环语句S的数据重用距离分别如公式（4）和（5）所示：

由公式（5）可知，循环语句S数据重用距离为语句中所有数组的最大重用距离。

通过以上分析可知，图1（b）示例的循环语句S中RDB最大。当RDB小于某级cache的大小时，说明数组B[k][j]两次重用之间所有访问的数据都可以放入该级cache中，则数组 B[k][j]在该级cache中能够得到重用。因为RDA和RDC都小于RDB，当数组B[k][j]得到重用时，A[i][k]和C[i][j]也一定得到重用。因此，定义循环语句S的数据重用距离为：RDS=max(RDA,RDB,RDC)。当RDS小于某级cache大小时，除去无法避免的第一次访问数据冷失效外，语句S中的数据都能够在该级cache中得到重用，从而获得局部性收益。

当块内循环语句S的数据重用距离RDS小于某级cache大小时，说明语句S中的所有数组均能在该级cache中得到重用，因此可以将整个分块的工作集映射到该级cache，以发掘块内的局部性收益。以图1（b）的代码为例来说明分块内工作集大小的计算，循环层i、k、j构成一个分块，块内包含参与运算的数据总共有数组 A[i][k]的 I×K个元素，数组B[k][j]的K×J个元素和数组C[i][j]的I×J个元素，故一个分块的工作集大小为：I×K+K×J+I×J。因此，可以建立一个基于程序局部性的分块因子(I,K)的搜索空间，如公式（6），其中 SizeL2、SizeL2和 SizeL3分别为L1、L2和L3级cache的大小。

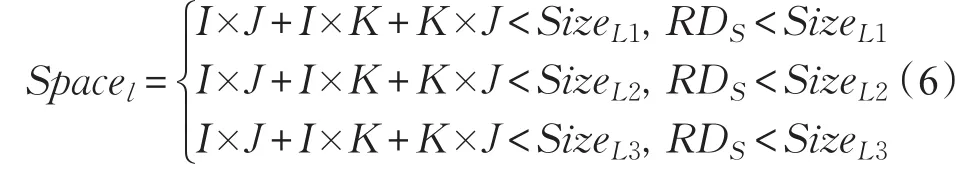
考虑到多级cache架构的特点，对于同时存储数据和指令的cache，根据文献[5]的处理方式，将可用于数据存储的容量设为该级cache容量的75%。对于r个核共享的cache，将可用于数据存储的容量设为该级cache容量的1/r。

（2）并行粒度

当采用多核对程序进行并行计算时，多核之间的负载均衡对并行收益有较大影响。文献[5]提到当每个核处理的分块数量大于2时，程序的并行收益能够得到保证，且多个核之间也是相对负载均衡的。本文通过大量实验也证实了这一点。

以图1（b）的程序为例，最外层循环是iT，该层循环迭代的数目为。当使用r个核并行执行程序，granularity表示分配给每个核的负载数目（即分块数目）时，为了保持良好的并行粒度，则应该满足公式（7）：

2.2.2 优化目标函数

数据在cache中的重用次数（Reuse Count，RC）越多，局部性收益越大，因此本文采用数据的重用次数来度量嵌套循环的局部性收益。以图1（b）的循环为例，通过公式（4）可以得到一个分块内语句S中数组B的重用距离最大，在数组B得到重用的同时，数组A和数组C都得到了重用。定义主导数组为执行语句中重用距离最大的数组，图1（b）中的主导数组为数组B，则主导数组带来的局部性收益可以代表整个分块的局部性收益。由于不同分块内的数组重用情况相同，因此研究一个分块内数组B的重用情况，可以代表整个程序的局部性收益。下面依然以图1（b）的代码来说明RC的计算过程。

假设公式（6）为L2 cache建立的搜索空间，即RDS

根据以上分析，当RCB取最大时，分块能够得到最大局部性收益。

通过以上分析，可以得到选择最优分块因子大小的过程。首先针对向量化收益，求出可向量化循环层的分块因子J。然后通过公式（6）和（7）建立分块因子(I,K)的搜索空间，并在搜索空间中找到使得公式（8）中RCB最大的分块因子(I,K)。最后组合得到的(I,K,J)即为最优的分块因子大小。其中在搜索空间中寻找分块因子时，为了更好地利用空间局部性，K的取值全部为CLS的倍数，CLS表示一个cache行能包含数组元素的个数。

3 VEC-TSS算法的应用

VEC-TSS算法可以作为一个独立的分块因子选择模块，嵌入到其他针对嵌套循环优化的工具中，例如PLuTo。PLuTo[8]是一款优化嵌套循环的代码转换工具，它本身并不提供TSS策略，只采用默认32的分块因子大小，但其为研究人员预留了重写分块因子的接口。本文将VEC-TSS算法在PLuTo中进行了集成和应用。图3展示了PLuTo的框架和循环代码转换流程，以及VECTSS算法在PLuTo中的模块位置，如图中虚线框所示。

图3 VEC-TSS算法在PLuTo中的应用

此外，相关的实现包含以下三部分。

（1）嵌套循环的可向量化识别。由于VEC-TSS算法的适用对象是可向量化的嵌套循环，因此第一步需要判断嵌套循环是否具有可向量化循环层。在PLuTo的结构体hyperplane_properties中定义变量vec，用来标记每个循环层是否可以向量化。PLuTo中存在发掘分块后程序可向量化循环层的函数pluto_pre_vectorize_band（）。借鉴以上函数可以实现函数pluto_pre_vectorize（），用来识别分块前程序各循环层是否可以向量化。

（2）VEC-TSS算法模块。如果嵌套循环存在可以向量化的循环层，则调用VEC-TSS算法。PLuTo工具利用Candl模块和isl模块，将程序的特征信息提取到多面体模型中，如问题规模、数组个数、数据类型、数组下标及循环层顺序等。VEC-TSS模块把以上信息作为输入，计算得到最优分块因子。为了使得计算结果能够被调用，定义全局结构体vec_tile_size来存储计算结果。

（3）调用VEC-TSS算法的结果。PluTo预留的重写分块因子接口为tile.sizes文件，PluTo通过函数read_tile_sizes（）读取tile.sizes文件中的各循环层分块因子。故可以通过修改函数read_tile_sizes（），使得PLuTo自动调用结构体vec_tile_size中的数据来进行代码分块。

4 实验分析

为了验证VEC-TSS算法的有效性，本文在一台Intel Xeon E7-4820服务器上进行了实验。该服务器具有4个8核的处理器，每个核拥有32 KB的L1级和256 KB的L2级cache，每个处理器具有16 MB的共享L3级cache；SIMD单元为256 bit；运行64位服务器版的CentOS 7.1.1503操作系统；采用icc 15.0.2编译器，编译选项为O3 parallel openmp。实验使用的PLuTo版本为pluto-0.11.4。

本文从PLuTo的程序集PLuToBench和多面体编译优化领域的PolyBench 3.2基准测试集[9]中选取了8个可以向量化的基准测试程序。其中测试程序matmul、dsyrk、dsyr2k、lu和trisolv的操作数为双精度浮点型，测试程序tmm、corcol和covcol的操作数为单精度浮点型。

4.1 病态问题规模结果与分析

不同问题规模的嵌套循环会有不同的最优分块因子。本文首先选取了一系列病态规模的程序进行测试，将VEC-TSS算法与目前先进的SICA算法[11]和TTS算法[13]进行比较。为了验证算法的有效性，排除线程数目的影响，本组测试程序均采用8线程执行。图4展示了分别采用三种算法的分块程序相对于未分块的原始程序的平均加速比。观察图4可知，随着问题规模的扩大，VEC-TSS算法的优势逐渐明显。这是由于随着问题规模的增大，可向量化的数据量也明显增加，向量化技术带来的优势更加显著，VEC-TSS算法能够使嵌套循环的向量化收益最大，比其他两个算法更具有优势。

图4 病态问题规模时VEC-TSS算法平均加速比

此外，表1展示了问题规模为3 199时各测试程序的分块因子。观察表1可知，各基准测试程序通过三种算法得到的分块因子类似，是由于这些基准测试程序虽然具有不同的循环结构和循环体，但是数据重用距离大小和嵌套循环中工作集大小却高度相似。

另外，通过VEC-TSS算法分块后的测试程序tmm、corcol和covcol的加速比较为突出。这是因为这三个程序的操作数为单精度浮点型，相较于双精度浮点型来说，向量寄存器中可以存放的数据更多，导致分块不恰当时，更容易产生数据非对齐问题。VEC-TSS算法能够更好地解决这个问题，相较于其他算法，性能更加优越。

表1 问题规模为3 199时的分块大小

4.2 可扩展性结果与分析

循环分块技术不仅能够改善程序的局部性，还能够开发程序的并行性。为了测试VEC-TSS算法对分块后程序并行可扩展性的影响，本文在问题规模为3 199时，分别采用线程数为1、4、8、16和32测试了分块后程序的加速比，结果如图5所示。

图5 VEC-TSS算法对程序并行可扩展性的影响

观察图5可以发现，随着线程数的增多，分块后程序的加速比近似表现为线性增长，这说明采用VEC-TSS算法的程序具有良好的并行可扩展性。究其原因有两方面：第一，VEC-TSS算法考虑到了多核共享L3 cache的情况，将L3 cache的容量均分给多个核，故分块后程序在多线程并行处理时，线程间不会竞争使用L3 cache；第二，VEC-TSS算法通过并行粒度分析限定最外层循环的分块因子，使得每个核分配到的循环块个数大于2，保证了多核之间的负载均衡。此外，测试程序lu和trisolv的并行可扩展性却不理想，如表2所示。这是因为程序本身具有较好的局部性，在多线程并行执行时，反而容易造成伪共享，增加了数据一致性开销。

表2 lu和trisolv的多线程加速比测试结果

本文仅采用Intel的CPU进行实验验证。但是本文提出的VEC-TSS算法同样适用于与Intel具有相同SIMD扩展指令集的AMD CPU[17]，以及具有相似SIMD扩展的国产飞腾、申威等处理器[18-19]。

5 结束语

本文针对病态规模的嵌套循环经过循环分块后会产生许多非对齐数据访问，从而影响自动向量化收益的问题，提出了一种VEC-TSS算法。该算法对于大规模的嵌套循环具有较明显的优势，且采用该算法分块后的循环具有良好的并行性。目前该算法仅适用于CPU处理器，对于具有向量化处理优势的GPU并不适用。下一步将会考虑GPU架构的特点，并将该算法扩展到GPU架构中。