不可达顶点剪枝算法及其在最短路径中的应用
李 艳,王阳阳,张红岩,武优西
1.河北工业大学 经济管理学院,天津 300401
2.河北工业大学 人工智能与数据科学学院,天津 300401
1 引言
可达性查询用于判定图G中从一个顶点u出发是否存在可以到达另外一个顶点v的路径[1-4]。由于其是传感器网络或生物信息网络中核心操作之一,因此,近年来其成为研究者普遍关注的热点问题[5-6]。在某些情况下,仅仅知道是否可达的意义不大,因为在诸如传感器网络中,信息可能会伴随路径长度呈现指数形式衰减,因此需要判断其在一定距离内的可达性,进而提出了k步可达性查询,其是指从顶点u到顶点v在k步是否可以到达[7-8]。在这些研究中,较好的方法是预先为图中每个顶点建立索引或索引区间,并依据索引或索引区间实现顶点的快速剪枝,从而实现快速判别是否k步可达。如Yildirim等人[9]提出了GRAIL算法,其是在有向无环图上通过不同的深度优先遍历方式为每个顶点附加两个区间标签L1和L2来减少误判率;Cheng等人[7]提出了利用最小顶点覆盖集来解决有向无环图中任意两点之间k步可达性查询的k-reach算法;周军锋等人[8]在GRAIL算法的基础上提出了BiRch算法,进一步提高了算法的查询速度。
但上述研究均是在无权图上进行的研究,显然在实际应用中,通常需要面对加权图,例如在实际的物流配送网络中,通常需要考虑配送节点间的距离、时间和成本等因素[10],其核心实质是最短路径问题。尽管最短路径问题是一个经典问题,并已有多种求解方法,如经典的Dijkstra算法和Floyd算法,此外还有A*算法[11]、SPFA算法和Bellman-Ford算法等[12]。但是随着现代经济水平的发展,图的规模不断增大,其结构也日趋复杂[13-14],其依然是众多学者关注的热点,如文献[15]对二阶最短路径问题的计算复杂性和近似求解算法进行了研究;文献[16]从云服务查询角度出发,对最短路径问题进行了研究;文献[17]研究了实时交通信息下城市动态网络的车辆路径优化问题,考虑实际路径中两种交通拥堵情形,在初始路径安排与实时路线调整相结合的情况下,解决物流路径问题;文献[18]研究了一种两阶段随机网络流模型,在风险价值模型上扩展进行风险预测,对配送目标顶点的位置和需求信息不确定情况下的物流配送路径问题进行了研究;为了提高寻优速度,文献[19-20]采用蚁群-聚类策略确定搜索半径,实现了自适应路径动态规划。
如果可以对不可达的顶点进行剪枝,从而缩减图的规模,则可以提高最短路径算法的计算效率。受GRAIL算法[9]的启发,本文提出了一种基于剪枝策略的最短路径算法(Shortest Path based on Pruning strategy,SPP)。该算法为图中每一个顶点u建立三个索引:最早到达索引Sx(u)、逆向最早到达索引Sy(u)和最晚到达索引Sz(u),进而快速判断出图中顶点间的不可达性,达到了缩减图规模的目的。该方法建立索引并剪枝无效顶点的时间复杂度和空间复杂度分别为O(n+e)和O(n),这里n和e分别表示图中顶点的数目和边的数目。该方法可以与传统的Dijkstra算法、Floyd算法和A*算法相结合,从而有效地提高这些算法的计算性能,实验结果验证了本文方法的正确性与可行性。
2 问题描述及求解方法
2.1 问题描述
在一个有向无环图中,从起始顶点出发,根据一定的距离约束条件,对图中顶点的不可达性进行判断,并对不可达顶点进行剪枝,来缩减图的规模。在剪枝后的图中,应用相应的算法寻找最短路径。为了实现这一目标,本文给出了如下形式化定义:
定义1对于图G中任意两个顶点u和v,若从顶点u出发存在一条路径可达v,则说明u可达v,用u→v来表示,反之说明u不可达v。若在顶点u到v之间存在代价C可达的路径,即u到v之间的路径总代价小于等于C,则说明u在代价C内可达v,用u→cv表示,反之说明u在代价C内不可达v。
为了实现上述可达性判断,本文提出了建立索引的方法,并运用这些索引实现了有效的剪枝策略,对不必要访问的顶点进行剪枝,从而缩减图的规模,达到在图中快速查找最短路径,提高算法计算效率的目的。
2.2 索引的构造
文献[9]在无权的有向无环图内研究了k步可达性查询,受该文献构建索引的方法启发,本文对加权有向无环图中的每一个顶点u建立三种索引:最早到达索引Sx(u)、逆向最早到达索引Sy(u)和最晚到达索引Sz(u)。由于为每个顶点增加3个索引属性值,因此一共创建了3×n个索引属性值。依据最晚到达索引Sz(u)可以确定从源顶点到目的顶点的最短路径上界h。如果从源顶点到某个顶点的最早到达索引Sx(u)或逆向最早到达索引Sy(u)超过该上界h,则表明该顶点一定不在最短路径上,可以被剪枝。
定义2最早到达索引Sx(u)是指从入度为0的顶点访问到该顶点的最小代价,其计算方法是:所有入度为0的顶点的索引值Sx(u)均为0,其余顶点的索引值Sx(u)为该顶点的所有入度顶点的索引值Sx(t)加上对应路径的权值后取最小值,即:

定义3逆向最早到达索引Sy(u)是指从出度为0的顶点反向计算访问到该顶点的最小代价,其计算方法是:所有出度为0的顶点的索引值Sy(u)均为0,其余顶点的索引值Sy(u)为该顶点所有出度顶点的索引值Sy(t)加上该路径的权值后取最小值,即:

定义4最晚到达索引Sz(u)是指从入度为0的顶点访问到该顶点的最大代价,其计算方法是:所有入度为0的顶点的索引值Sz(u)均为0,其余顶点的索引值Sz(u)为该顶点的所有入度顶点的索引值Sz(t)加上对应路径的权值后取最大值,即:

例1下面以图1为例来说明以上三个索引值的计算方法。图1中入度为0的顶点有1、11和20,这三个顶点的Sx(u)值为Sx(1)=Sx(11)=Sx(20)=0。由于顶点2只有一个父顶点为顶点1,因此其索引值Sx(2)=0+2=2。对于顶点4来说,它有两个父顶点分别为顶点3和12,且它们的索引值分别为Sx(12)=4和Sx(3)=4,由于Sx(12)+2=4+2=6
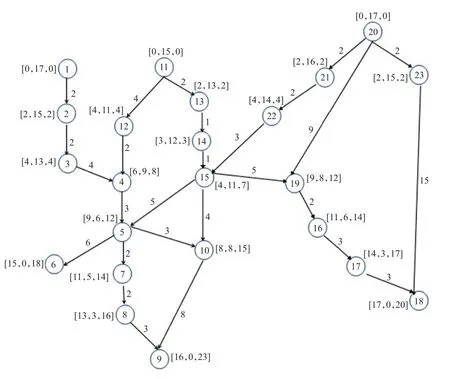
图1 具有三种索引的有向无环图
具体索引建立算法如下:
算法1索引建立算法
输入:加权有向无环图的邻接矩阵w[i][j](0 输出:索引序列Sx(u),Sy(u),Sz(u) 1.fori=1ton 2. 按照公式(1)计算Sx(u); 3. 按照公式(2)计算Sy(u); 4. 按照公式(3)计算Sz(u); 5.end for 6.returnSx(u),Sy(u),Sz(u); 本文通过定理1来预先确定出从顶点u到顶点v的最短距离上界h。定理2证明了以最短距离上界h为半径画圆,在圆外的顶点t不在从顶点u到顶点v的最短路径上。最后,通过定理3证明了圆外顶点t是可以被剪枝的顶点,从而可以将顶点t删除以达到缩减图规模的目的。 定理1令h=Sz(v)-Sz(u),从顶点u到顶点v的最短距离dis(u,v)≤h。 证明反证法,假定dis(u,v)>h。由定义4可知,从入度为0的顶点到达顶点u的最大代价为Sz(u)。从顶点u出发到顶点v的最短距离为dis(u,v),因此从入度为0的顶点经过顶点u到达顶点v的代价为Sz(u)+dis(u,v)>Sz(u)+h=Sz(u)+Sz(v)-Sz(u)=Sz(v),即从入度为0的顶点经过顶点u到达顶点v的代价大于Sz(v),这与定义4,Sz(v)是从入度为0的顶点到达顶点v的最大代价矛盾。因此最短距离dis(u,v)≤h。证毕。 定理2 令d1=Sx(t)-Sx(u),d2=Sy(u)-Sy(t),对于图中的每一个顶点对(u,t),若d1>h或d2>h,则顶点u到顶点t之间在距离h内是不可达的,即u→ht不成立。 证明反证法,假定d1=Sx(t)-Sx(u)>h且顶点u到顶点t在距离h内是可达的。通过索引进行判断,可知从入度为0的顶点抵达u的最小代价为Sx(u),由于顶点u到顶点t在距离h内是可达的,因此从入度为0的顶点到达顶点t的最小代价上界为Sx(u)+h,即Sx(t)≤Sx(u)+h,这与Sx(t)-Sx(u)>h矛盾,假设不成立,因此顶点u到顶点t在距离h内是不可达的。同理可证当d2>h时,顶点u到顶点t在距离h内也是不可达的。证毕。 定理3在计算从顶点u到顶点v最短距离的过程中,若u→ht不成立,则顶点t可以被剪枝。 证明反证法,假定顶点t在顶点u到顶点v最短路径上,因此dis(u,v)=dis(u,t)+dis(t,v)。若u→ht不成立,即在代价h下,从顶点u不可达顶点t,因而顶点u到达顶点t的最短距离大于h,即dis(u,t)>h。而这与定理1即dis(u,v)≤h矛盾。因此,顶点t不是最短路径上的顶点,可以被剪枝。证毕。 例2以图1为例来说明如何利用三种索引对图中的顶点在特定距离约束下的不可达性进行判断。例如在计算顶点11到顶点15的最短路径时,h=Sz(15)-Sz(11)=7-0=7,对于图中的顶点5来说,d1=Sx(5)-Sx(11)=9-0>7,因此可判断出顶点11到顶点5在距离7内是不可达的,这时就可以对顶点5进行剪枝。但是对于图中的顶点12来说,由于d1=Sx(12)-Sx(11)=4-0=4<7且d2=Sy(11)-Sy(12)=15-11=4<7,则顶点12不可以被剪枝。应用此方法可以快速对图中的顶点在特定距离约束内的不可达性进行判断。 根据网络中顶点的三种索引值,对顶点之间的不可达性进行判断,并对不可达顶点进行剪枝。基本思路为:给定顶点对(u,v),根据两顶点的最晚到达索引值之差计算出该路径的距离约束h,并依据定理2对顶点之间的不可达性进行判断,对不可达的顶点进行标记。具体算法如下: 算法2剪枝算法 输入:Sx(u),Sy(u),Sz(u),顶点u和v 输出:顶点标记序列status[t] 1.h=Sz(v)-Sz(u); 2.fort=1ton 3.if(Sx(t)-Sx(u)≤h&&Sy(u)-Sy(t)≤h)then 4.status[t]=true; 5. else 6.status[t]=false; 7.end if 8.end for 9.returnstatus[t]; 本文算法在计算过程中,首先根据算法2中得到的顶点状态值进行判断,若status[t]为真,则在最短路径求解过程中可以对顶点t进行访问;若status[t]为假,则对顶点t进行剪枝,即在求解最短路径的过程中,不再访问顶点t,以此来减少算法需要访问的顶点数量,达到缩减图规模的效果,从而提高了计算效率。 例3以图1中的索引为例,来说明SPP算法的计算过程。在计算顶点11到顶点15的最短路径的过程中,首先根据最晚到达索引值Sz(u)计算路径距离约束值h=Sz(15)-Sz(11)=7-0=7。应用最早到达索引和逆向最早到达索引进行判断,可以将5、6、7等10个顶点剪枝。在剪枝后的图上应用A*算法计算最短路径,可获得最短路径序列为11→13→14→15,最短路径距离为4,在这一计算过程中只需要访问10个顶点。然而,在原始的图上应用A*算法可求得最短路径序列仍为11→13→14→15,路径距离也为4,但该计算过程需要访问18个顶点。通过对比,不难发现SPP算法可有效减少算法的计算量,提高了计算效率。 具体算法如下: 算法3 SPP算法 输入:加权有向无环图的邻接矩阵w[i][j],顶点u和v 输出:最短路径dis(u,v) 1.调用算法1,生成Sx(u),Sy(u),Sz(u); 2.调用算法2,计算status[v]; 3.将status[v]中值为false的顶点去掉; 4.调用最短路径求解算法,在剪枝后的图上求解最短路径。 在剪枝后的图中分别应用Dijkstra算法、Floyd算法和A*算法对最短路径进行计算形成SPP(Dijkstra)、SPP(Floyd)和SPP(A*),其中A*算法的估值函数通过计算顶点对之间最晚到达索引值Sx(u)的差值得到。 与传统算法相比,本文算法增加了算法1和算法2,因此分析算法1和算法2的时间复杂度与空间复杂度即可。 定理4算法1索引建立算法和算法2剪枝算法的时间复杂度分别为O(n+e)和O(n),这里n和e分别表示图中顶点的数目和边的数目。 证明由于在关键路径求解问题中,其需要计算从起始顶点到指定顶点的最大路径长度,而这与本文中最晚到达索引Sz(u)是类似的,此外本文最早到达索引Sx(u)是计算最短路径长度,显然三者计算时间复杂度是一致的。而关键路径问题中最大路径长度的时间复杂度为O(n+e),因此,可知最晚到达索引Sz(u)以及最早到达索引Sx(u)的计算时间复杂度为O(n+e)。此外,逆向最早到达索引Sy(u)是最早到达索引Sx(u)的逆运算,因此其时间复杂度也为O(n+e)。故算法1索引建立算法的时间复杂度为O(n+e)。 由于为每个顶点均建立三个索引值:Sx(u),Sy(u),Sz(u),因此h=Sz(v)-Sz(u)和(Sx(t)-Sx(u)≤h&&Sy(u)-Sy(t)≤h)均为简单计算,进而可知算法2中第1行和第3行的时间复杂度为O(1)。又由于算法2中顶点t的循环次数为n次,因此算法2的时间复杂度为O(n)。证毕。 定理5算法1索引建立算法和算法2剪枝算法的空间复杂度均为O(n)。 证明显然算法1索引序列Sx(u),Sy(u)和Sz(u)以及算法2的顶点标记序列status[t]的空间复杂度均为O(n),此外在算法1的求解过程中,还需要引入堆栈,而堆栈的大小也是O(n)。因此算法1和算法2的空间复杂度均为O(n)。证毕。 本文建立索引并剪枝顶点的时间复杂度与空间复杂度分别为O(n+e)和O(n)。 本文采用文献[21]中西安雁塔区路网为实例,该物流配送网络中含有66个顶点如图2所示。图中顶点用数字符号表示,各路径的距离值作为图的权值,最终转化成一个加权有向无环图。限于篇幅,本文略去权值数据。 图2 物流配送网络图 3.2.1 算法正确性验证 为了验证本文剪枝算法的正确性,在图2中选取了12组数据进行测试。表1给出了选取的起点与终点以及原图的最短路径和剪枝后顶点间的最短路径。此外,表1还给出了依据定理1计算最短路径上界以及应用本文方法在图中剪枝顶点的数目。 表1 SPP算法计算结果 表2 采用Dijkstra算法的对比 表3 采用Floyd算法的对比 表4 采用A*算法的对比 此外本文采用了Dijkstra算法、Floyd算法和A*算法等三种最短路径计算的经典算法对本文剪枝算法的正确性进行验证,表2、表3和表4分别给出了Dijkstra算法与剪枝后的SPP(Dijkstra)算法、Floyd算法与剪枝后的SPP(Floyd)算法以及A*算法与剪枝后的SPP(A*)算法在剪枝前后访问顶点数目、循环次数和最短路径计算时间等指标的对比。 通过上述实验结果不难发现:SPP算法可以正确、有效地剪枝掉部分无用顶点,来缩减物流配送网络的规模。表1显示出SPP算法所剪枝的顶点均不是最短路径上的顶点,因此剪枝前后两点间最短路径结果不变。例如从顶点24到顶点59的最短距离计算中,在剪枝36个顶点情况下,最短距离依然为8.15 km。产生这种现象的原因是:由定理1、2和3可知,这种剪枝节点策略是安全的,剪枝部分无用节点后,不改变两点间最短路径的结果,从而验证了本文的剪枝算法的正确性。此外,通过表2、表3和表4可知,经过本文算法的剪枝,对Dijkstra算法、Floyd算法和A*算法等多种算法计算最短路径的性能均有提升。例如应用Dijkstra算法计算从顶点24到顶点59的最短路径时需要访问顶点数量由106个减少到42个,算法循环次数也由40次降低到17次,计算时间也由92 ms缩减到83 ms,其余实验也呈现完全相同的现象。这些实验结果充分地验证了SPP算法剪枝的正确性和有效性。 为了进一步检验本文中所建索引的性能,本文按照文献[9]建立索引区间的方法,为图中的每个顶点建立了先序和后序遍历索引区间,分别记作Lu[x,y]和Ru[x,y]。然后与本文提出的三种索引组合进行剪枝形成SPP-D算法,SPP-D算法与SPP算法的区别在于将算法2中第三行修改为: 其中If条件内的前两个并且运算就是实现文献[9]的索引区间方法的剪枝,其余部分一致,这里不再赘述。 在采用SPP-D算法剪枝后的物流配送网络中分别应用Dijkstra算法、Floyd算法和A*算法对最短路径进行计算形成SPP-D(Dijkstra)、SPP-D(Floyd)和SPP-D(A*)。为了验证SPP算法与SPP-D算法的性能,图3给出了两种算法剪枝顶点数量对比结果。图4至图6分别展示了采用Dijkstra算法、Floyd算法和A*算法下,SPP与SPP-D算法计算顶点数目及循环次数的对比结果。图中采用(x,y)形式描述实例,其中x和y分别代表起点和终点。此外表5从索引构造时间和最短路径平均计算时间角度进行了对比。 图3 SPP-D与SPP算法剪枝顶点数量对比 图4 Dijkstra算法下SPP-D与SPP计算顶点数目及循环次数对比 图5 Floyd算法下SPP-D与SPP计算顶点数目及循环次数对比 图6 A*算法下SPP-D与SPP计算顶点数目及循环次数对比 表5 索引构造时间及最短路径平均计算时间对比ms 通过上述实验结果不难发现:SPP-D算法和SPP算法具有相同的性能,但是SPP算法是最有效的剪枝算法。具体分析如图3~6。 (1)SPP-D算法和SPP算法具有相同的性能。尽管SPP-D算法比SPP算法剪枝的顶点数量要多,但是在应用Dijkstra算法、Floyd算法和A*算法计算最短路径时,SPP-D算法和SPP算法计算的顶点数量及循环次数在相同实例上均是相同的。造成这种现象的原因是:(1)SPP算法剪枝掉顶点是相同分枝下,但是肯定不可以到达的顶点,这样可有效降低算法的计算量;(2)SPP-D算法是在本文方法SPP的基础上,增加了文献[9]的先序和后序遍历索引区间,这两种索引是针对可达性问题构建的,其能够有效地剪枝图中不同分枝上的顶点,而这些顶点对最短路径的计算没有影响。简而言之,这两种索引剪枝的顶点与求解最短路径无关,因此对Dijkstra算法、Floyd算法和A*算法的求解过程中计算顶点数量和循环次数不构成影响。在例3的基础上,举例说明如下:由于SPP-D算法是在SPP算法基础上增加先序和后序遍历索引区间,因此SPP-D算法不仅能够剪枝与SPP算法一样的5、6、7等10个顶点,而且还可以多剪枝1、2、3、20、21、22和23共7个顶点。而这7个顶点均在顶点11到顶点15的最短路径中不可抵达的分支上,因此剪枝这些顶点与否,对于最短路径的求解并无影响。 (2)SPP算法是最有效的剪枝算法。由于SPP-D算法需要比本文的SPP算法多建立2组索区间,共4个索引,因此SPP-D算法在索引建立时间上也会相应地增加。表5实验结果也表明,SPP-D算法构建索引时间为6.56 ms,比SPP算法的3.56 ms多了3 ms,从而验证了本文的SPP算法是适合加权图的高效剪枝算法。此外,表5显示出最短路径平均计算时间由114 ms缩减到103 ms,平均缩短时间为11 ms,而SPP算法索引构建时间仅为3.56 ms,这说明通过建立索引的方法,可以缩减最短路径计算时间。更为重要的是,索引一经构建以后可以重复使用,从而验证了本文算法的可行性和有效性。 本文研究了基于剪枝策略的有向无环图最短路径求解问题,提出了SPP算法,减少了最短路径求解过程中需要访问的顶点数量,并将该算法与传统最短路径算法相结合,从而提高了传统最短路径算法的计算效率,进而实现了最短路径的快速求解。SPP算法在加权有向无环图上构建了三种索引:最早到达索引、逆向最早到达索引和最晚到达索引。在定理1中通过最晚到达索引来预先确定出加权有向无环图中从顶点u到顶点v的最短距离上界h。在定理2中,以上界h为半径画圆,证明了圆外的顶点t不在从顶点u到顶点v的最短路径上,这里画圆的方式采用最早到达索引和逆向最早到达索引。定理3理论证明了圆外顶点t是可以被剪枝的顶点,从而可以将顶点t删除以达到缩减图规模的目的。上述三个定理理论证明了SPP算法可以实现有向无环图的最短路径中不可达顶点的快速剪枝。最后以物流配送网络为例进行了大量对比性实验验证了本文方法的高效性。未来将关注如何在有向图中或无向图中构建索引,实现有效地剪枝,从而实现有向图中或无向图中最短路径的求解。2.3 剪枝算法
2.4 SPP算法
2.5 复杂度分析
3 实验结果及分析
3.1 实验数据

3.2 实验结果与分析




3.2 .2 算法高效性验证
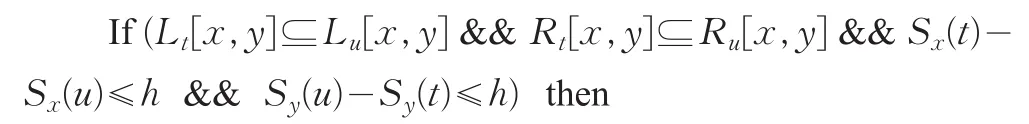





4 结束语

