有“核仁”的数学课

周卫东

摘要：一节好的数学课应该意识到“桃核”里“核仁”的價值。这“核仁”应该是暗含于教学内容中的基本原理、数学思想和方法以及“结构”。其实，“核仁”亦即数学本来的味道。

关键词：数学课;数学味;基本原理;思想方法;结构

许多人都喜欢吃桃，但吃完桃以后，可别忘了里面还有一个小小的核，核里面还有一个小小的核仁。会品味的人不会轻易把桃核丢掉，而是拿小锤子轻轻敲开，尝尝那个滋味不一样的核仁。

我想，一节好的数学课，应该意识到“桃核”里“核仁”的价值。那么，这“核仁”应该是什么呢？让我们走进几则课例，慢慢地品味。

丁爱平老师执教的《三位数乘两位数》一课中有“核仁”。

下课前约5分钟，丁老师说：“同学们，丁老师翻阅了四年级下册后面的教材，关于整数的乘法，没有出现我们预计的四位数乘两位数或三位数乘三位数。这是为什么呢？是因为编教材的专家忘记了吗？”

深度思维一定是“好问题”驱动出来的。不一会儿，学生纷纷发表自己的想法：“不是忘记了，是因为不需要再编下去了。”“它们计算的原理是一样的。”“无论四位数乘两位数还是三位数乘三位数，都只是在三位数乘两位数的基础上多了一步而已。”“所有多位数的乘法，都是按照‘先分后合的原理计算的。”……顺着学生的思路，丁老师充分发挥她简笔画的优势，流畅快捷地勾画出一棵“大树”（见图1）。这是一棵关于整数乘法计算的内在关联的“结构树”，这棵“树”的生长“基因”就是多位数乘法计算的基本原理。

不难看出，这里的“核仁”就是暗含于教学内容中的基本原理。

沈珏如老师是一位刚工作不久的新教师，她执教的一年级数学课《10的分与合》中也有“核仁”。

课上，她放手让学生自由进行10的分与合的尝试。学生操作时，她轻轻带上了一句：“小朋友们要边摆边想，怎样才能做到不重复、不遗漏呢？”这实际上是在提醒学生要做到“有序”思考。所有摆法都被发现后，她继续引导学生思考：“这么多摆法，我们有什么好办法记住它们呢？”“真好，你们看到了各种摆法中的变化，那么有没有什么地方不变呢？”顺着学生的回答，她相机在黑板上留下了“不变”“变”两个关键词（课堂板书见图2）。

真的难得，刚工作三个月的新教师，面对入学才三个月的学生，课堂上已悄然见到了“有序”“变与不变”等策略、思想的影子。

随堂观摩《多位数的读写》一课，李洪丹老师带领学生研究一道数学题：“用4个6、4个0组成一个8位数，最多读几个0？”一位学生在尝试、交流中汇报：“4-1=3，最多读3个0。”李老师精神一振，果断接过该生的发言：“感觉到你这种方法挺好的，其他同学明白他的想法吗？”然后让该生到前面来讲述理由。在勾勾画画的板书（见图3）中，全班学生都弄懂了其中的道理：0只有在6与6的间隔中才能读出来，4个6之间共有3个间隔，所以最多读出3个0。

原来，普通的数学题中也有策略、思想的痕迹。

著名数学家弗里德曼说：“数学的逻辑结构的一个特殊的和最重要的要素就是数学思想，整个数学科学就是建立在这些思想的基础上，并按照这些思想发展起来的……数学的各种方法、思想是数学最重要的部分。”这句话道出了数学教学的关键、核心所在。

是的，这里的“核仁”就是暗含于教学内容中的数学思想和方法。

我在执教《认识公顷》一课时，也努力寻找“核仁”。

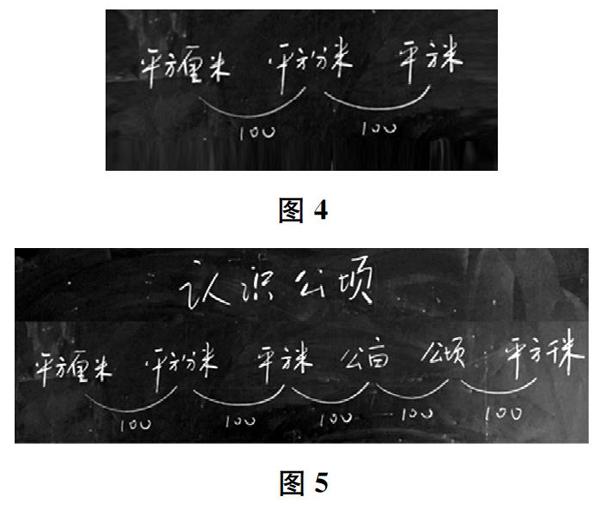
我先带领学生复习学过的面积单位和它们之间的进率，形成图4所示的板书。随后引导学生想象：“如果继续创造下去，应该是什么面积单位？”学生顺向迁移：平方十米、平方百米、平方千米……在此境况下，我相机揭示：“真好！你们创造的这些单位，在数学中都是存在的，只不过它们有的还有别的名称，比如，平方十米也叫公亩，平方百米也叫公顷，平方千米不变。”顺势形成图5所示的板书。

皮亚杰指出：“全部数学都可以按照结构的建构来考虑，而这种结构始终是完全开放的……当数学实体从一个水平转移到另一个水平时，它们的功能会不断地改变，对这类实体进行的运演，反过来，又成为理论研究的对象，这个过程在一直重复下去，直到我们达到了一种结构为止，这种结构，或者正在形成更强的结构，或者再由更强的来予以结构化。”

“结构”是数学的基本特征，教数学中的“结构”才算是抓住了数学教学的根本。

由此看来，此环节中的“核仁”当是数学中的“结构”。

行文到此，脑海里浮现出齐白石先生的一幅画（见图6）：一张纸从上到下什么都没有，在这张纸三分之一的地方画了一片秋天的叶子，叶子上面趴着一只头朝下的蝉，叶子旁边写了两句诗“鸣蝉抱叶落，及地有余声”。

绝了！这只蝉快掉地上了，还有声音。这是一幅有声音的画。

课同此理，我一直有一种美好的期待：我们的数学课堂能否也多些这种意境呢？如果可能，是不是与课中的“核仁”有关呢？

其实，“核仁”亦即数学本来的味道！有“核仁”的课并不复杂，应是数学课的一种应然追求。好的数学课，不应在所谓各种形式的“创新”上卖力，不应在所谓方式方法的“变革”上折腾，而应本真地对待学科，真诚地面对儿童。