基于变胞机构原理的举升式舱门机构运动学建模与仿真

丁晨，汪俊，陈庆波，唐建平，葛张森，姚燕生

(安徽建筑大学 机械与电气工程学院，安徽 合肥 230601)

0 引言

变胞机构最早被发现于包装礼品盒简化的机构，由英国伦敦大学国王学院戴建生教授于1998年首次提出，与传统机构不同，变胞机构运行过程中拓扑结构与自由度呈阶段性变化[1]。从变胞机构被发现至今，运用其原理进行机械创新设计越来越多[2-7]，同时对其相关理论研究也在不断完善。

近年来对于变胞机构的理论研究主要分为两个方向，一种是结构学研究，如运用拓扑图法与邻接矩阵法来描述杆组之间的连接关系的改变，PAN等[8]用拓扑图法直观描述了具有变胞功能的电动装载机构的构态变化，但拓扑图法并不能建立各个构态之间转换的运算法则。WU 等[9]基于改进邻接矩阵法使变胞机构各独立构态之间可以用变胞方程传递杆组之间的连接特性，进而建立了一套完整的运算法则，使变胞机构各构态之间可以进行定量的数值计算。

另外一种是运动学研究，张云娇等[10]用旋量法分析了多种并联变胞机构，张满慧等[11]用四元数学模型分析了一种典型的空间变胞机构。然而这些运动学分析方法主要适用于分析空间变胞机构。对于约束变胞机构的研究目前涉足的学者较少。李树军[12]等用运动循环图和等效阻力梯度模型描述平面约束变胞机构，并指出目前尚未有有效的理论分析平面约束变胞机构。本文分析了一种平面约束变胞举升舱门机构，用几何参数法建立机构运动方程组，以运动学方法描述平面约束变胞机构构态变化，并确定了举升力与构件参数。本文的分析方法补充了平面约束变胞机构理论。

借助于结构学与运动学分析方法，新型变胞机构不断涌现，本文设计的这种举升舱门机构用途也十分广泛，如移动房车举升式太阳能电池板、电动开窗器、舞台升降门机构等等。

1 机构运行机理描述

为了清晰描述该机构的运动过程，给出该机构的运动简图，结合机构自由度变化，阐述机构运行机理。图1 中，θ1、θ2、θ3分别是机构运行至构态1、构态2 和构态3 的状态。本舱门要求垂直升降，即要求θ3为π/2。

由平面机构自由度G-K公式[13]

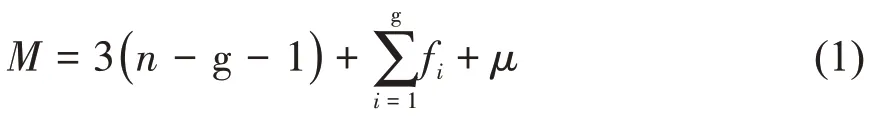
(1)式中M为机构自由度，n表示机构构件总数，g 表示机构运动副总数，f表示第i个运动副的自由度，μ是机构中过约束数目。

当机构运转到θ1点时，处于构态1，滑块并未压缩弹簧，滑块与舱门看成一个整体，此时机构构件数目为4，运动副数目为4，此时机构自由度为：

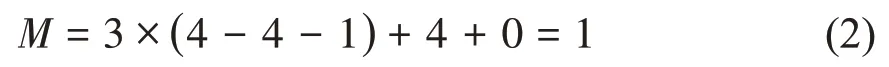
当机构运转到θ2点时，处于构态2，滑块开始压缩弹簧，此时机构构件数目为5，运动副数目为5，此时机构自由度为：

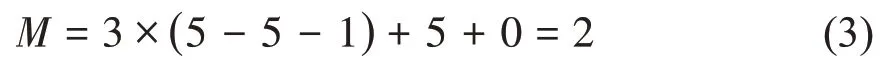
当机构运转到θ3点时，处于构态3，舱门门受阻，将舱门与机架看做一个整体，滑块仍在滑动，活动构件数目为4，运动副数目为4，此时机构自由度

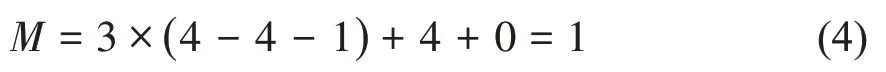
当举升舱门转动到构态3 时，机构通过推杆内的丝杠自锁。

基于文献[14]，对变胞机构类型的定义，该机构属于第Ⅲ类变胞机构，此时机构的拓扑图如图2。

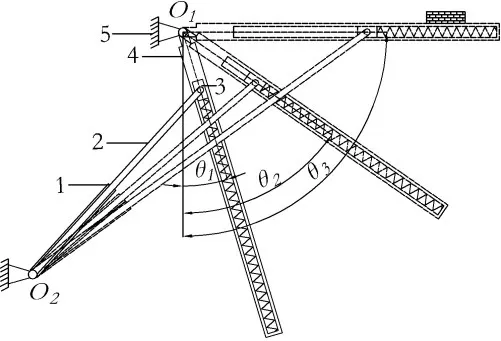
图1 机构运动简图

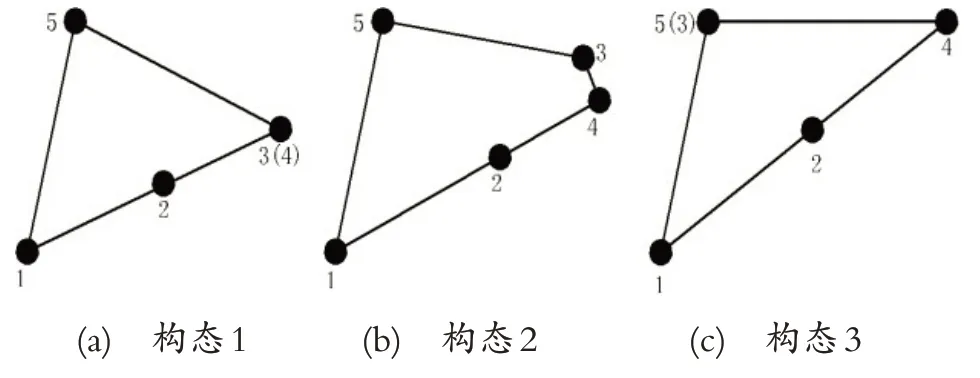
图2 机构拓扑结构变化

传统机构运行过程中拓扑结构不发生变化，而变胞机构运行过程中拓扑结构呈现阶段性变化，这正是变胞机构与传统机构的本质区别。拓扑结构的改变类似于生物学细胞分裂，变胞机构也由此得名，基于以上分析，该机构完整运行周期的构态变化可以用表1 表示。

2 机构运动学建模

2.1 基于运动学模型的构态变化分析

以下分析计算中各参数均用字母代替，θ代表舱门转角，θ*代表构态1 向构态2 变换时的邻界角，L代表O1与O2直线距离，α代表舱门初始状态时与L的夹角，β代表θ与α之和，β∈[0,π),γ代表推杆与舱门夹角，r代表推杆与门的支撑点B到O1点距离，a代表初始状态下推杆支撑点B点到舱门回转中心O1的距离，d表示B点处的合力向回转中心O1所作的合力臂，b代表舱门长度，X代表弹簧原长，x代表弹簧形变量，G代表舱门自重，h代表O1到O1的垂直距离，e代表O1到O1的水平距离。l代表电动推杆长度，l̇代表电动推杆伸出速度，l̈代表电动推杆伸出加速度。θ̇代表舱门角速度，θ̈代表舱门转动角加速度，θ*代表构态变化临界角，d1代表驱动力力臂，d2代表舱门重力力臂，d1min代表驱动力最小力臂，d1max代表驱动力最大力臂，d2代表重力力臂，d代表B点处合力力臂，M( )FB表示B点所受合力矩，F代表推杆驱动力，FB表示推杆支撑舱门B点所受的合力，F*代表临界处的推力，F1代表驱动力力臂为最小力臂时弹簧所受压力。F2代表驱动力力臂为最大力臂时弹簧所受压力，机构原理简图如图3 所示。

表1 机构完整运行周期构态变化

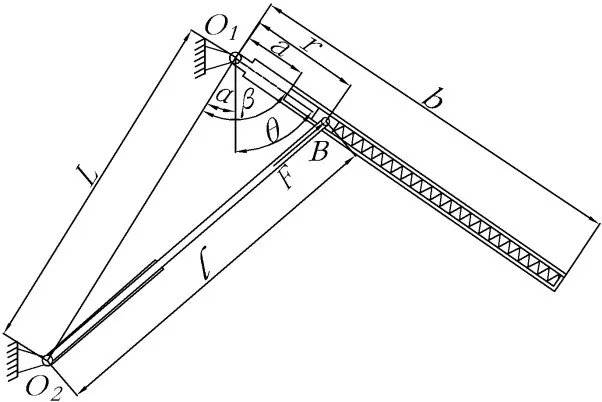
图3 机构原理简图

本变胞机构杆长l与机构各参数之间的关系可表示为：

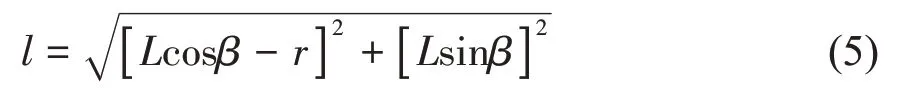
基于链式法则[15]，由(5)中的变量l与θ的1阶、2 阶导数方程，可得机构运动学方程组

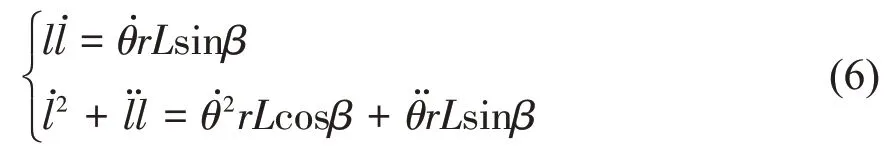
由于电动推杆匀速伸出，l̇为定值，则l̈= 0，由(6)式得到

同样由(6)式得到

将(7)代入(8)式得

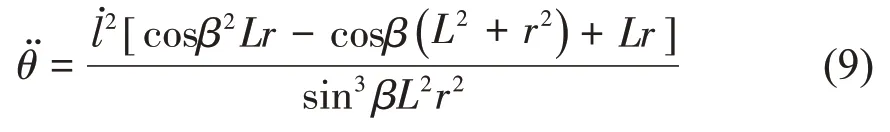
(9)式中，基于分子变量cosβ 的方程

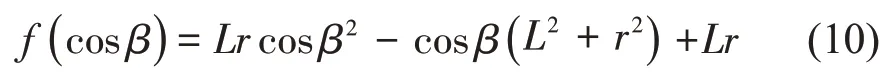
( 10 )式中方程f( cosβ)的函数抛物线开口朝上，其根为

机构处于构态1 时a=r，本例中a＜L,cosβ∈[-1,1]，(11)式中方程的根cosβ2无意义。因此cosβ1=a/L为方程f( cosβ)的根。f( cosβ)函数开口朝上，且根cosβ1大于零，函数为凹函数，f( cosβ)函数曲线先经过四象限后经过一象限，当β∈[0,π/2]时，(9)式中的分母大于零，θ̈的正负性取决于分子，因此

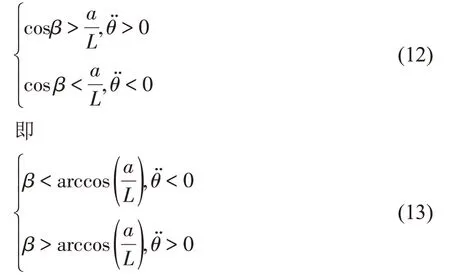
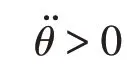
舱门上各点运动状态相同，角加速度相等，将运动状态分析向推杆支撑舱门的B点简化，由刚体转动定理，B点处的合力矩可表示为

B点所受合力矩M(FB)的正负性取决于θ̈的正负，而B点处的合力对回转中心O1所作的合力臂

因此B点处的合力可表示为

根据轴力正负性原则，FB＜0 时，B点所受合力对其定轴O1点施加压力，此时弹簧无形变。FB＞0 时，B点所受合力对其定轴O1点施加拉力，此时弹簧开始受压。基于以上分析机构构态变化可以大致用图4 表示。

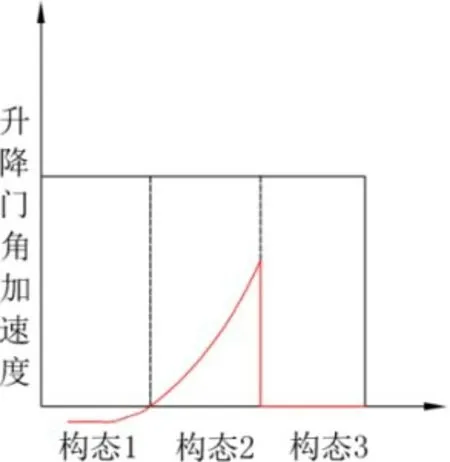
图4 机构构态变化与舱门角加速度的关系

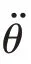
表2 基于运动学模型的机构构态变化

以上基于运动学模型分析了的机构构态变化，以下分析实现举升功能的举升力与构件参数。

2.2 举升力与构件参数分析

若机构并不是变胞机构，机构是传统机舱门机构，机构内没有弹簧构件，驱动力F应当随舱门重力力矩增大而增大，传统举升舱式门受力简图如图5 所示。

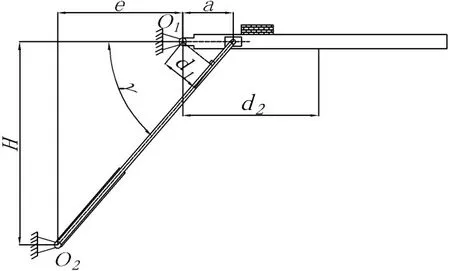
图5 传统举升舱门机构受力简图

由力矩平衡法

推杆的驱动臂是

重力臂为舱门中心线到O1的水平距离，可表示为

与推杆之间的角度为

所以推杆所需的推力是

得益于机构可变胞的优势，以构态1 向构态2变化临界角处的驱动力F，通过压缩弹簧形变量x增大驱动力力臂d1，使驱动力力矩与舱门重力力矩达到平衡，这样机构可实现由临界状态向构态3 的变化，受力简图如图6 所示。

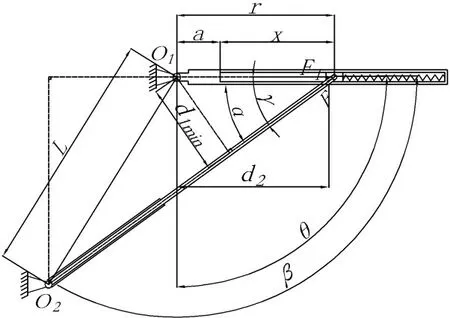
图6 最小驱动力臂时机构受力简图

根据力矩平衡法

舱门转动过程中重力臂始终位于舱门向地面所做投影线的中点对O1所做的垂线长度，重力力臂随转角增大而增大，重力臂可表示为：

如图6 所示，根据相似三角形原理，驱动力力臂d1与r的比值等于O2向舱门做垂直线长度与杆长的比值，因此推杆驱动力臂变化可表示为

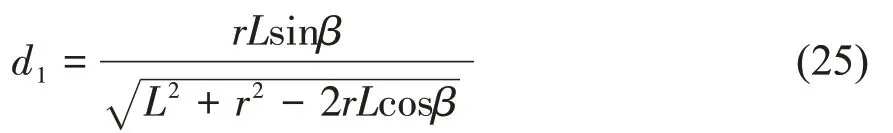
舱门转动到临界角θ*处，r=a，重力臂与驱动力臂均可由已知参数求得，因此机构由构态1 向构态2 变换临界点处的驱动力可表示为

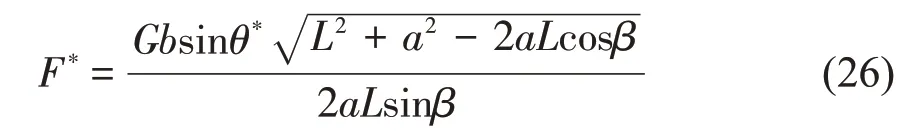
以临界角处驱动力驱动机构到构态3，驱动力F的力臂至少为

驱动力最小力臂与机构各构件参数关系为

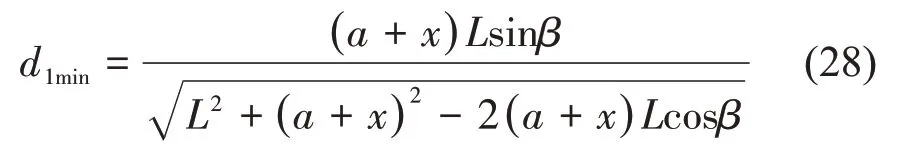
由式(27)、(28)可得驱动力为最小力臂时，弹簧最小形变量xmin，舱门被举升后受阻，驱动力力臂可以大于d1min，当弹簧构件选取空气弹簧时，弹簧最大压缩比可为1，即弹簧压缩量为弹簧原长时，驱动力力臂可达到最大值，如图7 所示。

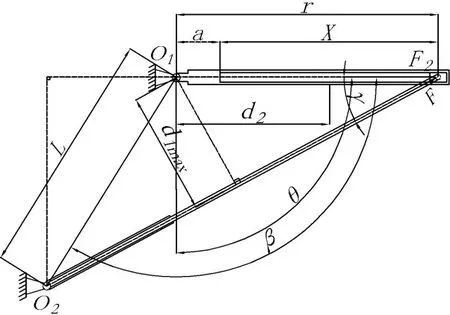
图7 最大驱动力臂时机构受力简图

驱动最大力臂可表示为

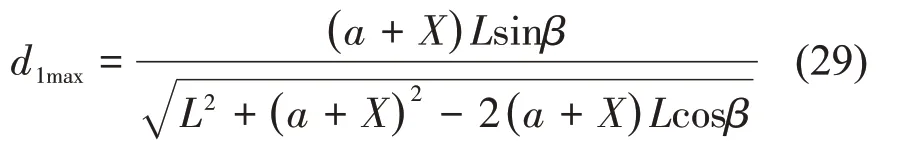
由上述分析，推力F的力臂d1的取值范围取值范围为

当驱动力臂是d1min时，推杆与舱门所呈夹角为

此时弹簧所受压力为

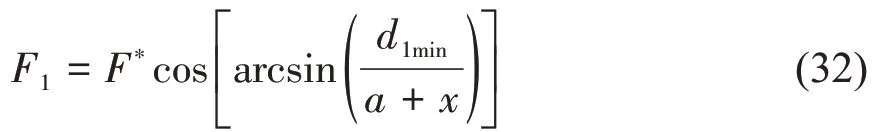
当驱动力臂是d1max时，推杆与舱门所成夹角为

此时弹簧所受压力为所受压力为

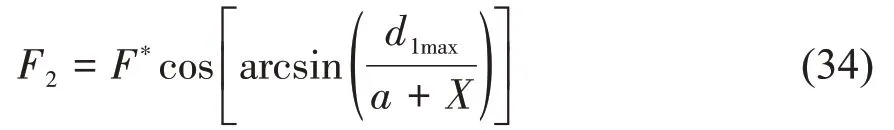
由胡克定律

弹簧刚度K的取值范围为

3 实例分析与Adams仿真

3.1 实例数值求解

基于实际案例，舱门各参数尺寸分别是X=0.75 m、L=1.06 m、e=0.71 m，h=0.86 m，a=0.15 m、b=1.0 8m、α=40°，G=1000 N。

由(18)、(19)、(20)、(21)、(22)式得到传统举升舱门所需举升力

F= 5 091.1688 N ≈5 091 N

由(17)式得到构态变化邻界角为

θ*≈41.87°≈42°

由(26)式得构态变化邻界角时推杆驱动力

F*= 2 360.699 N ≈2 361 N

以同等大小推力驱动机构到构态3，由(27)式最小力臂为

d1min= 0.16657 m ≈0.167 m

由(27)、(28)式，得弹簧最小形变量为

xmin= 0.1157 m ≈0.116 m

当驱动力为最小力臂时，由(31)式推杆与门的夹角为

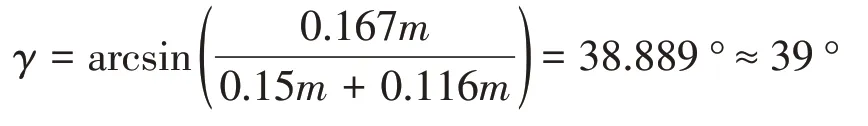
由(32)式，弹簧所受压力为

F1=2361N×cos39°=1834.8416N ≈1835N

此时弹簧刚度为

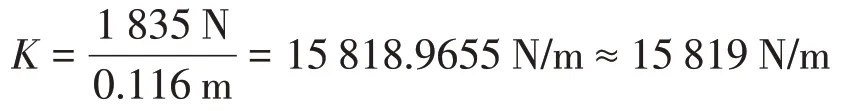
由(29)式得到最大驱动力臂

dmax= 0.39568 m ≈0.396 m

由(33)式，推杆与门的夹角为

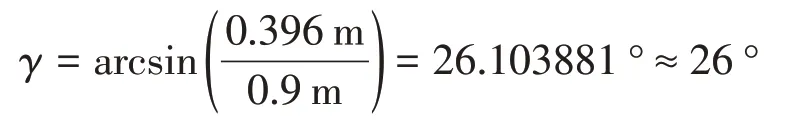
由(34)弹簧所受压力为

F2=2360N×cos 26°=2 121.1539 N ≈2 121 N

此时弹簧刚度为

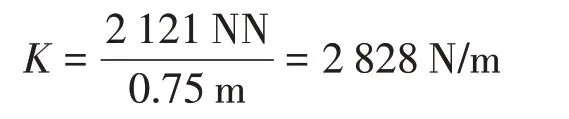
弹簧刚度K的取值范围为

[2 828 N/m,15 097 N/m]

3.2 ADAMS动力学仿真

Adams 是目前最适合对变胞机构进行运动分析的软件[16]。由上述实例数值分别建立优化前的机构与优化后的机构Adams 仿真模型。由于Adams 空间建模能力有限，借助UG 精确的空间建模能力，将机构模型上下方向按照Z轴方向建好，转换成Parasolid(x_t)格式，再导入到Adams 中。由于这种舱门是克服自重实现开合，为模拟现实中的环境，在Adams 中指定好各个活动部件质量，定义重力G的方向为Z轴负方向，机构仿真模型图如图8 所示。

图8 舱门等轴侧视图

根据活动门零部件自锁上的运动情况添加合理的约束关系，约束关系见表3。

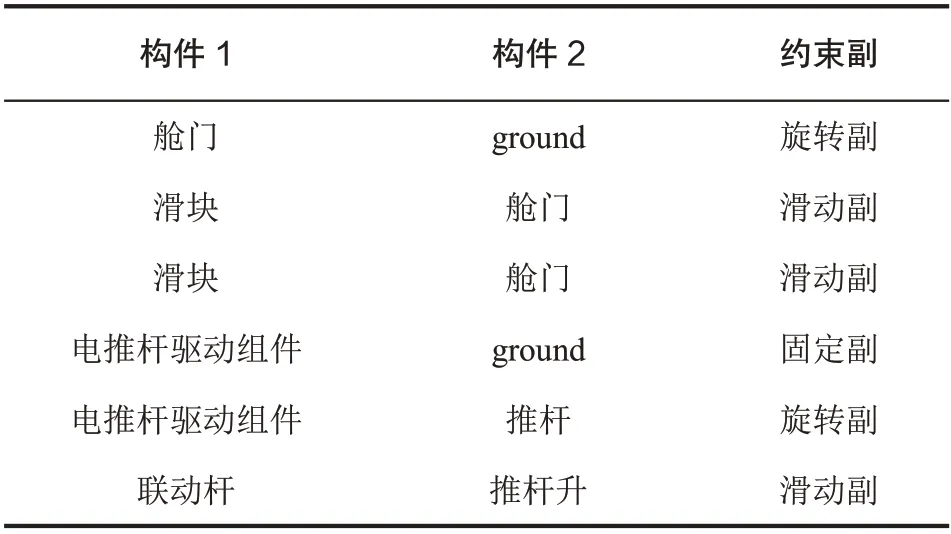
表3 变胞仓门各构件之间约束关系

添加约束后，根据运动学分析所得结果设置推杆驱动力以及弹簧刚度，驱动力设置为临界角处驱动力，弹簧刚度选取最大值15 097 N/m 时，仿真结果如图9-图11。

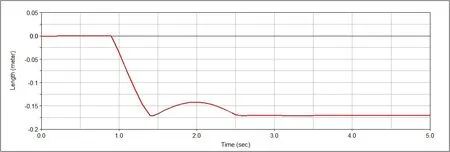
图9 弹簧形变量

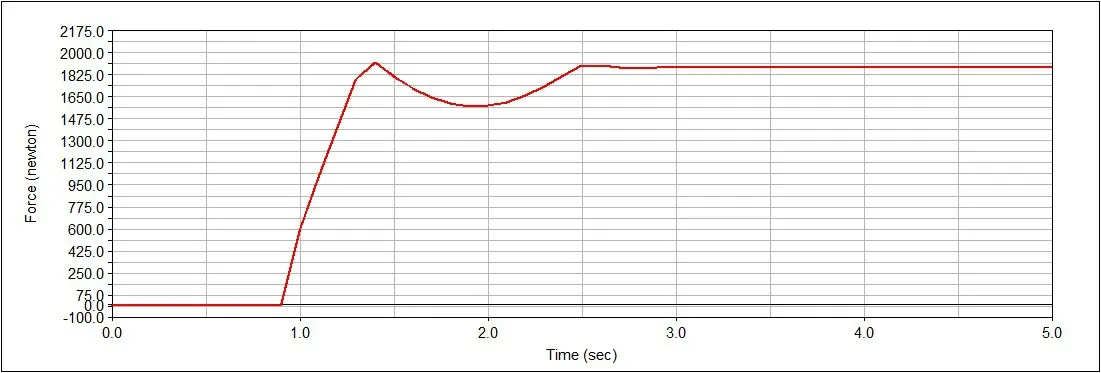
图10 弹簧受力变化

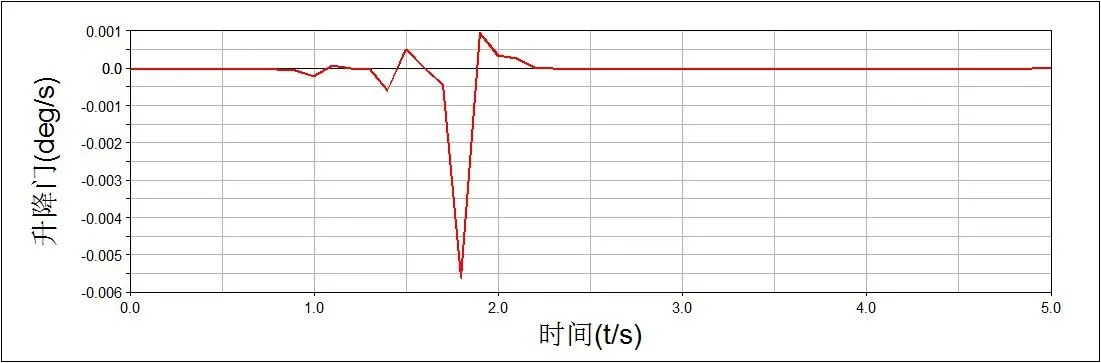
图11 舱门角加速度变化

同样当以临界角处推力驱动机构到构态3，弹簧刚度取最小值2 828 N/m 时，仿真结果如图12-图14。

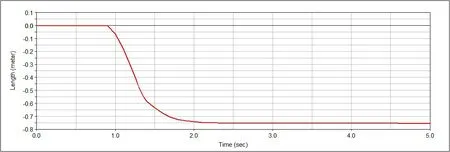
图12 弹簧形变

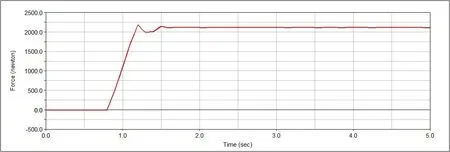
图13 弹簧受力变化

图14 舱门角加速度变化

传统舱门机构仿真模型与约束条件与变胞举升式舱门机构完全相同，机构内不添加弹簧构件，仿真结果如图15。

图15 传统舱门推杆举升力变化

从图9、10、12、13 可以看出弹簧所受最大压力和弹簧形变量与数值计算结果完全吻合。单从弹簧受力图与形变图只能看出机构运行过程中具有两种构态，第一构态为弹簧未受压力，无形变，第二构态为弹簧受压形变。分别结合图9、10 和图12、13 可以看出，当弹簧受到最大压力后，即舱门受阻后，弹簧仍然有形变量，说明机构运行过程中还具有第3 种构态，验证了机构运行机理分析的正确性。由图11、图14 可以看出，舱门角加速度经历由负转变为正再降为零的过程，与运动学分析结果一致。由图15 看出，传统举升舱门所需举升力为5 091 N，约为变胞举升舱门机构的2 倍。综合以上分析说明借助于变胞机构的优越性，以临界角处推力继续驱动机构运转是切实可行的，大大减小了举升力。

4 结语

本文对分析了一种基于变胞机构原理的举升式舱门机构，相比于传统举升舱门机构，在安装空间限定的情况下，可以以较小的推力举升机构，推力减小即可以使得电机的耗电量减小，又可使驱动组件的重量减轻，运输过程耗能会减少。目前较为常见的电动开窗器大批量安装时，均运用本文所运用的变胞设计方法，能大大减小电能的消耗，应用前景十分广泛。运用本文的分析方法，也确定了驱动该变胞机构构态变化所需举升力与构件参数。为该种机构应用推广提供了理论分析依据。