基于股票价格的股票差异性与相关性获取方法研究

程红梅

(安徽建筑大学经济与管理学院，安徽 合肥，230601)

0 引言

股票市场作为社会经济系统的“经济晴雨表”，其稳定性和健康性是国民经济健康稳定发展的内在要求，越来越多的学者关注以股票市场为代表的金融领域研究[1-6]。在综合因素的影响下，相关研究一般均将股票市场视作由交易账户、股票市场中的交易关系为基本元素的复杂网络[5-8]。股票价格的涨跌、股票交易量等股票市场的指征属性都可以在股票网络上体现，基于不同的复杂网络模型和超网络模型，股票市场的行为被细致地分析。

股票市场相关性研究中，以股票为点、股票之间的关系为边构造的股票网络模型已经成为股票相关性分析研究的重要工具。随着计算机软硬件性能的显著提升、大数据技术的普及以及人工智能研究的新进展[9-10]，基于股票网络的股票相关性分析被越来越多的研究所关注[1-3，7，8]。

本文的研究面向基于股票网络的股票市场行为分析，基于股票价格序列，研究了使用欧式距离计量股票差异性的原理与方法，并在实现股票差异性计量的基础上，讨论了基于股票差异性的相关性股票获取方法。本文的第二部分讨论了基于股价变化序列的股票距离的定义及其估计方法；第三部分对基于距离最佳逼近k维欧氏索引的股票相关性方法进行了描述；实验结果与分析在第四部分给出，第五部分对研究进行了总结并未来的研究进行了展望。

1 基于股价变化序列的股票距离及其估计

一只股票在交易期间内每个时刻的成交价格是该股票的特征时间序列。任意两只股票的差异性可以使用它们各自特征时间序列的距离度量。

设函数f:[0L]→R、g:[0L]→R是[0L]上的连续函数，即f(x),g(x)∈C[0L]，泛函G(f,g)如式(1)规定。

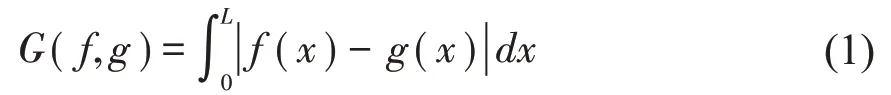
引理1：设泛函G(f,g) 如式(1)规定，则对∀f(x),g(x)∈C[0L]，G(f,g)≥0。且 当 且 仅 当f=g时，G(f,g)= 0。

证明：

(1) ∵对∀f(x),g(x)∈C[0L]，f(x),g(x)∈R

∴|f(x)-g(x) |≥0

∴对∀f(x),g(x)∈C[0L]，G(f,g)≥0。

(2) 又 对∀f(x)∈C[0L]，|f(x)-f(x) |= 0，故G(f,f)= 0。

(3) 再设∃f(x),g(x) ∈C[0L]，f≠g，

G(f,g)= 0，则：

∵f≠g

∴∃x0∈[0L]，f(x0)≠g(x0)，不 妨 设f(x0)＞g(x0)

∵f(x),g(x)∈C[0L]

∴∃0 ≤δ1＜δ2≤L,x0∈[δ1δ2]，对∀x∈[δ1δ2]，f(x)＞g(x)

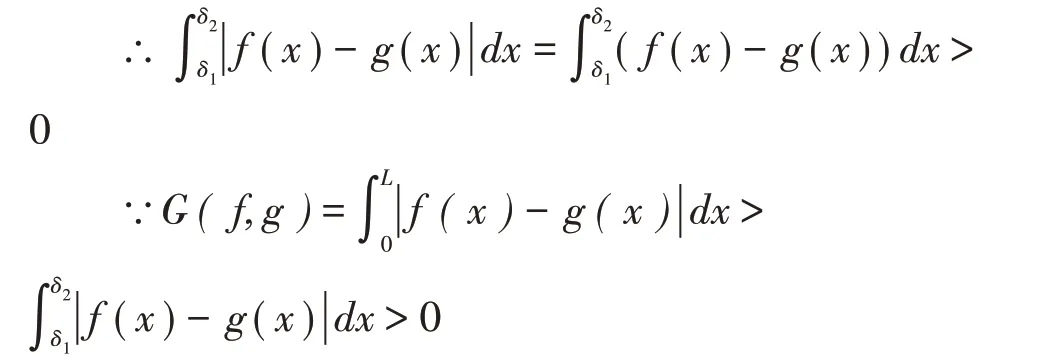
∴假设不成立，故G(f,g)= 0 且仅当f=g时。

∴综合(1)(2)(3)，引理成立。

引理2：设泛函G(f,g) 如式(1)规定，则对∀f(x),g(x)∈C[0L]，G(f,g)=G(g,f)。

证明：

∵对∀f(x),g(x)∈C[0L]，f(x),g(x)∈R，|f(x)-g(x) |= |g(x)-f(x)|

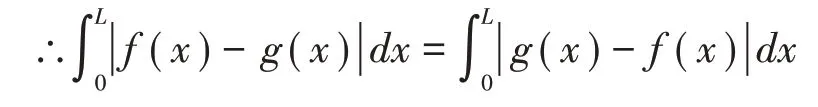
∴G(f,g)=G(g,f)

引理3：设泛函G(f,g)如式(1)规定，则对∀f(x),g(x),h(x)∈C[0L]，G(f,g)≤G(f,h)+G(h,g)。

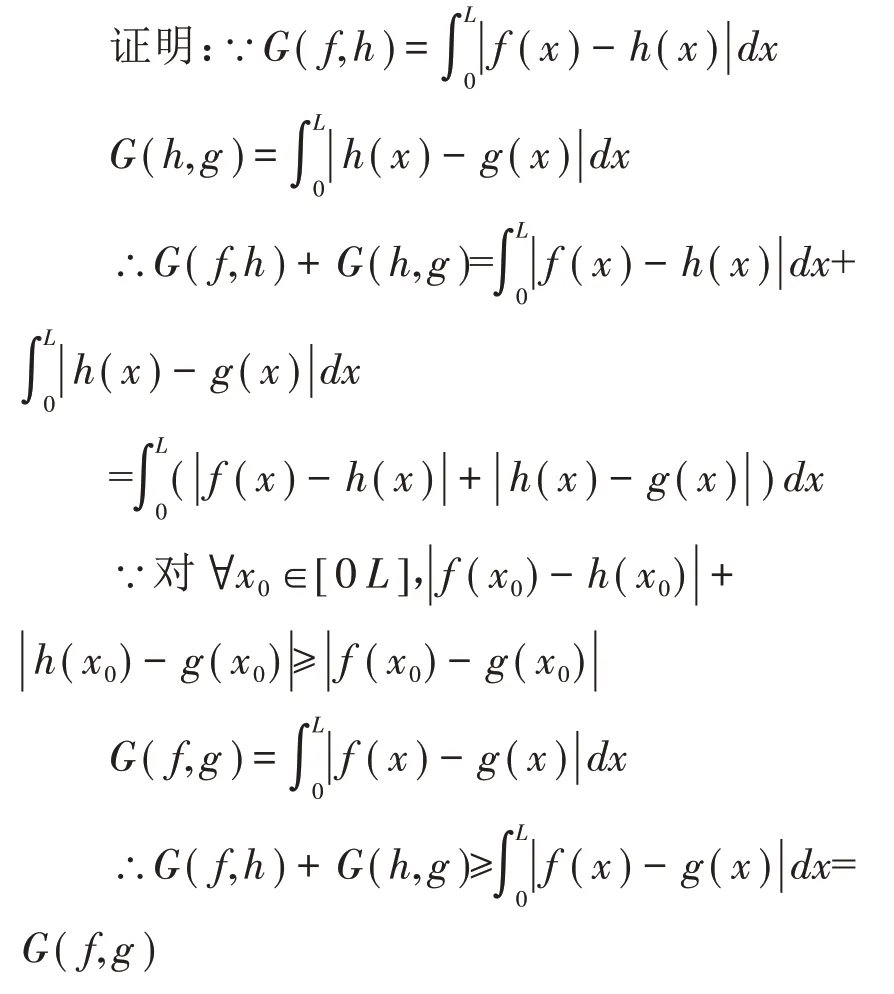
根据引理1～3，式(1)定义的泛函G(f,g)是函数f(x)到g(x)的欧氏距离，故函数f(x)、g(x)间的欧氏距离如定义1 规定。

定义1：设函数f:[0L]→R、g:[0L]→R是[0L]上的连续函数，泛函G(f,g)如式(1)规定，若G(f,g)= 0 当且仅当f(x)=g(x)，则G(f,g)是函数f(x)、g(x)间的欧氏距离。

进一步可以证明，对引理1，若不强调“当且仅当f=g时，G(f,g)= 0”，则对式(1)规定的泛函G(f,g)，函数f、g在区间[0L]上连续的条件可以不再要求。此时，泛函G(f,g)满足引理4。而根据引理2～4，函数f(x)到函数g(x)的泛化欧氏距离如定义2 规定。

引理4：设函数f:[0L]→R、g:[0L]→R是[0L] 上的函数，泛函G(f,g) 如式(1)规定，则对∀f(x),g(x)∈C[0L]，G(f,g)≥0。

证明：∵f:[0L]→R、g:[0L]→R是[0L]上的函数

∴f(x),g(x)∈R

∴|f(x)-g(x) |≥0

∴G(f,g)≥0。

定义2：设函数f:[0L]→R、g:[0L]→R是[0L] 上的 函 数，泛 函G(f,g) 如 式(1)规 定，则G(f,g)是函数f(x)、g(x)间的泛化欧氏距离。

对 函 数f(x),g(x)∈C[0L]，设0 =t0＜t1＜…＜tn-1＜tn=L， Δi=ti-ti-1，i= 1,2…n， 若G͂(f,g)如式(2)规定，则G(f,g)≈G͂(f,g)。显然，G͂(f,g)是对函数f、g的欧氏距离或者泛化欧氏距离G(f,g) 的估计，且max{Δi|i= 1,2…n}}越小，G͂(f,g)对G(f,g)的估计越准确。

一般的，对不同股票的价格序列，可以依据式(2)对股票的差异性进行估计。特别的，若股票价格的变化是连续函数时，依据式(2)估计的股票的差异性是股票间的欧式距离，而若认为股票的价格是非连续变化时，依据式(2)估计的股票的差异性是股票间的欧式泛化距离。

2 基于距离最佳逼近k维欧氏索引的股票相关性

交易时间内，市场内影响股票价格的因素众多，不同的因素对不同股票的价格影响程度不一。股票价格作为诸多因素影响的最终结果，不同股票价格的关联变化特性反映了不同股票间的内在联系，因此，股票价格的相关性是股票相关性的一种外在表现：当股票价格相关频繁发生时，相关股票应存在某种意义上的关联。一方面，股票价格的相关性可以使用股票价格序列的相关系数度量，而股票价格序列相关系数的计算需要确定股票价格的协方差，而计算协方差时，无论是序列的期望还是方差的精度都直接影响相关系数对股票相关性的准备程度的衡量，这意味着使用相关系数定量股票价格的相关性，需要较长时间段内的股票价格序列。而量化较短时间段的股票价格序列的相关性时，一般基于历史价格序列的均值进行估计[2]。另一方面，依据式(2)可以基于股票价格序列的欧式泛化距离量化股票价格序列的差异性，而股票价格序列的差异性越小，股票价格序列的相关性越大。进一步，若已知股票价格序列间的欧式泛化距离，还可以使用多维尺度分析技术将股票价格序列映射为2 维或3 维空间中的点，这样，就可以在2 维或3 维空间中通过观察股票价格序列对应点间的空间临近关系直观显示股票价格序列的相关性。

定义3：设L1、L2是股票S1、S2某一时间段内的同粒度股价序列，d(L1,L2)是序列L1、L2如定义2规定的距离。若对α＞0，d(L1,L2)≤α，则称股票S1、S2股价α相关。

定义4：设L1i、L2i是股票S1、S2第i 时间段内的同粒度股价序列，i= 1,2…n。若对任意0 ＜β≤1，股票S1、S2的股价α相关的次数不少于n×β，则称股票S1、S2β(α)相关。

定 义 5：设 数 据 集P={P1,P2…Pn}，对∀Pi∈P，若Qi=(qi1,qi2…qik)是k维欧氏空间中与Pi∈P对应的k维向量，则称Qi是Pi的k欧氏索引，而Q={Q1,Q2…Qn}则是P的k欧氏索引集。

设P={P1,P2…Pn}是给定交易时间内某个时间段内的n支股票的股票价格序列集，由定义2 知n支股票的距离可计算。

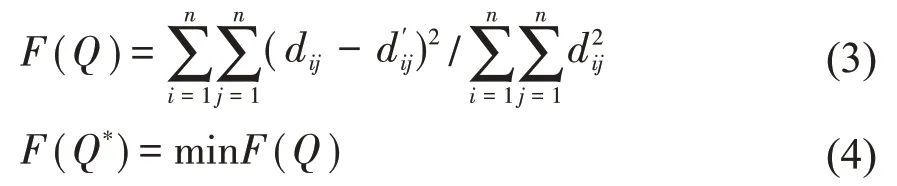
定义2 规定的股票价格序列集P的距离最佳逼近k维欧氏索引集可以使用多维标度分析(multidimensional scaling，MDS)方法求解。在k=2 或者k=3 时，可以将每支股票视作2 维或者3 维空间中的一个点从而直观的展示各支股票的空间相对位置，直观的表达股票的β(α)相关性。算法1 给出了基于股票价格序列集和距离最佳逼近k维欧氏索引集β(α)相关的股票获取过程的形式描述。

定义6 规定的股票价格序列集P的距离最佳逼近k维欧氏索引集可以使用多维标度分析(multidimensional scaling，MDS)方法求解。在k=2 或者k=3 时，可以将每支股票视作2 维或者3 维空间中的一个点从而直观的展示各支股票的空间相对位置，直观的表达股票的β(α)相关性。算法1 给出了基于股票价格序列集和距离最佳逼近k维欧氏索引集β(α)相关的股票获取过程的形式描述。

算法1：基于股票价格序列集和距离最佳逼近k 维欧氏索引集β(α)相关的股票获取过程

输入：股票价格观测窗口宽度L，阈值α、β，全部股票的价格序列矩阵Mmxn，维数k/*m 只股票，每只股票有n 个价格数据*/输出：相关的股票序列集RS

1)股票价格序列集合PS 置空；

2)for 每一只股票

从价格序列的第一个数值开始，自前向后逐一析取连续L个股票价格作为股票价格序列增加到股票价格序列集合PS 中；每只股票可构造p(=n-L+1)个股票价格序列。

3) 为PS 中的每只股票价格序列建立k维欧式索引；

4)使用全部股票价格序列的k维欧式索引计算每个观察时刻(共p个)全部股票的欧式距离矩阵dM；

/*dM 有p个元素，每个元素是全部股票的1个欧氏距离矩阵*/

5)依据dM 和α 计算每个观察时刻任意两只股票的相关性到bM；

/* bM 有p个元素，每个元素是记录每个观察时刻任意全部股票的相关矩阵；由于任意两只股票的距离不大于boundary 时股票相关，相关矩阵对应元素取值为1，否则为0*/

6)将bM 中的α 个相关矩阵累加到相关判别矩阵cM；

7) cM 中，若两只股票的相关性累加值不小于p×β，则记录这两只股票相关到RS 中。

3 实验结果与分析

实验选取了2017 年7 月12 日交易时间内，在沪深两市交易的25 支银行股票的每分钟的成交价格为数据源(每支股票共有240 个数据)。由于各股票的价格差异显著，实验使用每支股票的每分钟成交价相对开盘价的涨跌幅(=(成交价-开盘价)/开盘价)为实验数据。25 支股票的涨跌幅情况如图1所示，同时从图1 也可以观察出某些股票的成交价格的涨跌存在着一致性。

为验证算法1 的有效性，我们使用了依据式(2)计算的股票价格序列距离与算法1 中使用股票价格序列的k维欧式索引的距离作为对比。对比试验结果表明，在分别选取合适的α、β的前提下，两种方法均可以构造同样的相关股票数据集。例如，为获得相关股票集{民生银行600016，交通银行601328}时，算法1 使用的参数α、β分别取值为0.04 和0.99，而在直接使用股票价格序列距离时，参数α、β 分别取值为0.01 和0.9。实验中，股票价格观测窗口宽度L取值为10，即通过分析过去10 min 以来的股票成交价格来判断任意两只股票是否相关。

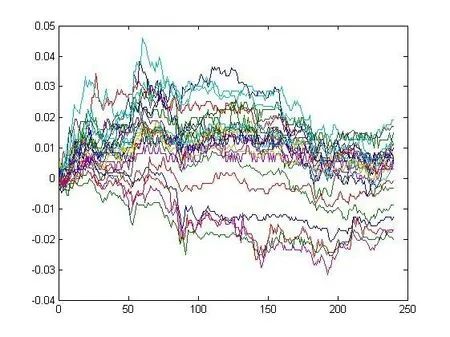
图1 25支银行股的涨跌

相比较直接使用股票价格序列距离获取β(α)相关的股票集，使用算法1 获取β(α)相关的股票集时，在维度参数k=2 或者3 时，可以在2 维平面或者3 维空间中直接展示各股票的相对位置。由于所使用的索引是k维欧氏索引，展示各股票的相对位置关系时，每只股票是所在空间中的一个点，而不同点间的距离直接反映了与每个点对应的股票的相关程度：点间的距离越小，对应股票的相关性越大。图2 给出了实验用25 只股票在2 维空间中的相对位置231 次叠加后股票空间的分布效果，这种效果是图1 中描述的25 支股票价格波动的另一角度的诠释。典型时刻25 只股票在2 维欧式空间中的相对位置关系由图3 的(a)-(h)子图给出。图3的每个子图中，图题为股票相对位置所处的时刻。显然，股票价格序列的k维欧氏索引能够直观的刻画股票的相关性。

4 结论与研究展望

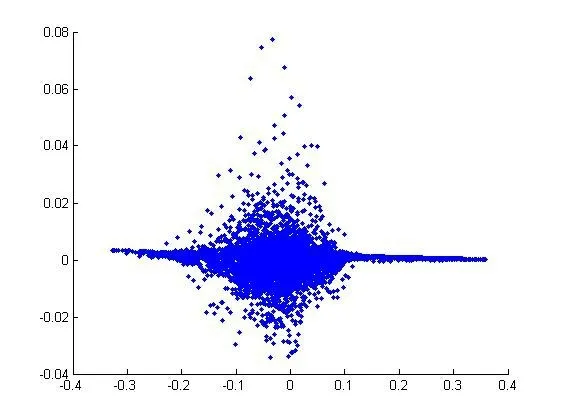
图2 股票相对位置叠加后的股票空间分布

图3 典型时刻股票的相对位置

股票的相关性检测是股票市场中异常行为监测与管理的基础，为获取正常交易的股票的相关性，本文基于股票价格序列定义了股票的距离和泛化距离实现了股票差异性的定量计算。基于定量的股票距离，本文使用多尺度分析技术实现了股票价格序列在k维欧式空间的索引：股票价格序列的k维欧式空索引一方面可以用于在2 维或3 维空间中直观的显示股票之间的差异性，另一方面还可以使得基于欧式距离的聚类或者分类技术有效的应用于股票数据的深度分析过程。同时，本文在股票股价相关的基础上定义了股票的β(α)相关，设计了获取β(α)相关股票的方法，实现了基于股票价格序列的相关性股票的有效获取。进一步，基于股票价格序列的β(α)相关的相关性股票的获取也为以股票为点、股票之间的关系为边构造的股票网络模型中边的有效描述提供了一种新量化手段。

关于股票相关性，本文仅仅考虑了股票间的正相关特性，负相关股票获取的模型与方法是未来必须关注的研究。同时，本文研究直接使用了股票的价格序列，已经进行的研究显示基于股票价格的变化可以更细致的揭示股票之间的内在关联特性，基于股票价格变化的股票相关性模型与相关股票获取方法设计是值得关注的研究。