不同力装置布局的双层剪叉式升降平台的比较分析
(闽江学院实验实训管理中心,福建 福州 350108)
0 引言
剪叉机构的基本单元为两杆交叉铰接而成,由基本单元在竖直方向上串联组成的剪叉式升降平台其有结构紧凑,平行升降,行程范围大,可靠性强的特点[1-2]。因此,在诸如货物垂直运输、零件装配、农业采摘、设备检修、高层作业等场景中具有广泛的应用[3-4]。根据驱动方式的不同可以将剪叉式升降机构分为液压式,气压式,电力驱动式3种。在推力装置的分布上可分为水平固定、竖直固定、双铰接固定3种方式[5]。在推力装置作用下,剪叉式升降平台将单层的升降距离进行多倍放大,以达到合适的工作高度,但随着层数的增加,剪叉升降平台对推力、行程的控制提出了更高的要求。在通常情况下,设计者希望能够在满足升降高度与升降载荷的前提下,驱动机构的推力越小,驱动机构的速度越稳定越好[6-7]。本文针对双层剪叉式升降平台,分别对推杆在与转动杆—基座双铰接固定、滑移杆—基座双铰接固定、水平固定的3种结构形式进行机构运动学与动力学分析,根据速度瞬心法与虚功原理求解机构运动学与动力学模型。并在应用案例中对3种结构形式下的5种推杆布置情境进行对比与分析,以此作为实际设计中的理论依据。
1 双层剪叉式升降平台与基本单元间的升降速度关系


图1 双层剪叉式升降平台Fig.1 Bi-layer scissor lift platform

(2)


(3)

(4)


(5)
可知杆CH与杆AD的瞬时角速度相等,进一步求得点H的速度:

(6)
即vh=2vd,双层剪叉式升降平台的升降速度为基本单元升降速度的两倍。因此,在分析双层剪叉式升降平台抬升速度时,仅需分析单层时的运动情况即可。
2 3种结构形式的剪叉机构运动学与动力学建模
在实际工程应用中,应根据剪叉机构的安装空间与用途进行设计。若为双层剪叉式升降平台,其基本形状固定,主要区别在于推力装置的布局与选型。推力装置一端铰接于基座,另一端铰接于基本单元其中一连杆,主要存在有如下3种结构形式:转动杆一基座双铰接固定、滑移杆一基座双铰接固定、水平固定。接着分别对这3种结构形式进行机构运动学与动力学分析。
2.1 转动杆一基座双铰接固定
转动杆一基座双铰接固定的结构形式如图2所示,存在有推力装置(推杆)与基座的铰接点位于剪叉机构右侧与内侧的两种情况。其特点在于推杆的K端铰接于基座上,K(L1,0),推杆另一端G点铰接于转动连杆OC上。推杆长度为g,G点到连杆OC中点的距离记为b。

图2 转动杆—基座双铰接固定Fig.2 Double hinged fixation between rotating rod and base
设平台HF的上升速度为vh,平面DC的上升速度为vd,推杆伸出速度为vg。杆OC绕O点转动,因此O点为杆OC的速度瞬心。C点分速度vcy与vd相等,由式(4)可知vc与vcy的夹角为α,可求得C点合速度vc为

(7)

(8)
连杆OC在推杆铰接点G的绝对速度vg′为
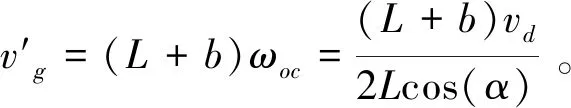
(9)
推杆速度vg为vg′的速度分解,vg′与vg的夹角记为β:

(10)
可求得推杆速度vg为

(11)
由式(6)可知vh=2vd,所以平台HF的上升速度vh为

(12)
进一步对剪叉机构进行动力学分析。所述铰接为理想约束,在负载W与推杆力T的作用下,整个剪叉机构处于平衡状态。根据虚功原理:在平衡力系作用下,质点系在刚性虚位移上所作功的总和等于零[10-11]。即
∑(Fixδx+Fiyδy+Fizδz)=0 ,
(13)
式中,Fix、Fiy、Fiz为作用于质点i上的x、y、z方向上的分力,δx、δy、δz为质点i上的虚位移。如图2所示,推杆推力在G处分解为
Tx=-Tcos(θ),Ty=Tsin(θ) 。
(14)
G的坐标值为
xT=(L+b)cos(α),yT=(L+b)sin(α) 。
(15)
经变分运算可得G点的虚位移为
δxT=-(L+b)sin(α)δα,δyT=(L+b)cos(α)δα。
(16)
负载W在施加处的作用力为
Wx=0,Wy=-W。
(17)
坐标值为
xW=0,yW=4Lsin(α) 。
(18)
经变分运算可得虚位移为
δxW=0,δyW=4Lcos(α)δα。
(19)
将式(14)~式(18)代入式(13)中,经整理可得推杆推力T

(20)

2.2 滑移杆一基座双铰接固定


图3 滑移杆—基座双铰接固定方式Fig.3 Double hinged fixation between sliding rod and base
设平面HF的上升速度为vh,由第1节分析可知,刚体一连杆AD的速度瞬心为C点,瞬时角速度为ωAD。连接CG两点,CG长度记为L2:

(21)
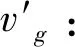

(22)
根据几何关系可求得推杆速度vg与vg′的夹角β:

(23)
可求得推杆速度vg为
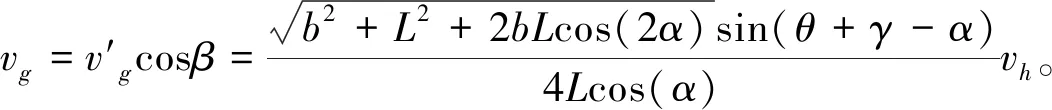
(24)
平面HF的上升速度vh为

(25)
进行剪叉机构动力学分析,推杆推力在G处分解为:
Tx=Tcos(θ),Ty=Tsin(θ) 。
(26)
G点坐标值为
xT=(L-b)cos(α),yT=(L+b)sin(α) 。
(27)
经变分运算可得G点虚位移为
δxT=(b-L)sin(α)δα,δyT=(L+b)cos(α)δα。
(28)
负载W、虚位移在x与y方向上的分解与上述式(17)~式(19)中所述情况相同。将所计算的虚位移与分解力代入式(13)中,经整理可得推杆推力T:

(29)

2.3 水平固定
水平固定结构形式如图4所示,其特点在于推杆的K端转动铰接于基座上,另一端转动铰接于滑移点A上,推杆长度为g。在水平固定时,推杆与基座的铰接点同样存在有位于剪叉机构的内侧与外侧时的情况,但这两种布局方式对推杆推力与运动速度并无影响,只是伸缩的方向不同而已。因此,只讨论推杆在外侧水平固定时的情况。
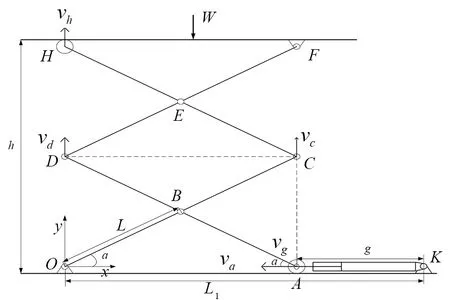
图4 水平固定方式Fig.4 The horizontal fixed mode
推杆伸出速度vg与A点的滑移速度相等,根据第1节分析可知,刚体AD的瞬时角速度ωAD为

(30)
平台HF的上升速度vh为

(31)
进行剪叉机构动力学分析。所述铰接为理想约束,在负载W与推杆力T的作用下,整个剪叉机构处于平衡状态。推杆推力在滑移点分解为
Tx=-T,Ty=0 。
(32)
A点坐标值为
xT=2Lcos(α),yT=0 。
(33)
经变分运算可得A处虚位移
δxT=-2Lsin(α)δα,δyT=0 。
(34)
负载W、虚位移与上述式(17)~式(19)中所分析的相同。将力分解与虚位移代入式(13)中,经整理可得推杆推力T:
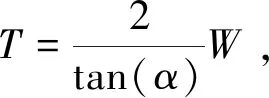
(35)

3 应用实例分析
在完成对剪叉升降平台推力装置的3种不同结构形式的运动/动力学建模后,现根据实际案例,对总共5种不同位置的推杆布局方式进行分析。所要应用场景为:设计一款双层剪叉式升降平台,可放置于皮卡车之类的中小型工具车后斗,用于将物品抬升至货架上。升降平台结构参数如表1所示。

表1 升降平台结构参数


表2 推杆与基座的铰接位置


(36)
最终得到推杆速度vg、推杆长度g、推力T与平台上升量△h的关系曲线,如图5~图7所示。可知,无论采取哪一种固定方式,平台在最低位置时,所需推力最大,随着高度的增加,推力逐渐减小。总体上,平台所需最大推力Tmax与推杆最大行程gmax负相关,所需Tmax越大时,gmax越小,所需Tmax越小时,gmax越大。

图5 采用转动杆—基座双铰接固定方式的推杆参数Fig.5 The push parameter about double hinged fixation between rotating rod and base

图6 采用滑移杆—基座双铰接固定方式的推杆参数Fig.6 The push parameter about double hinged fixation between sliding rod and base

图7 采用水平固定方式的推杆参数 Fig.7 The push parameter about the horizontal fixed mode


计算5种分布方式下的“所需最大推力Tmax”“推杆最大行程gmax”“所占空间L1”3个指标。按照指标数值大小,将布局方式分为5个等级,其中数值最小者记为1,最大记为5,依次进行排序,得到推杆不同布局方式时的性能比较,见表3。


表3 不同推杆布局方式的性能比较
4 结语
以双层剪叉式升降平台作为研究对象,阐述了单层剪叉平台升降速度与双层平台升降速度的关系。列出了推杆与基本单元连杆在铰接时的5种情况,即:位于右侧一与转动杆铰接、位于内侧一与滑移杆铰接、位于左侧一与转动杆铰接、位于内侧一与转动杆铰接、水平固定铰接,利用速度瞬心法与虚功原理建立机构运动学与动力学模型,得出了推杆速度与平台升速、平台负载与推杆推力的关系式。结合实例,对5种推杆布局方式进行计算,在绘制推杆参数曲线后进行比较分析,指出不同分布方式的优缺点,并根据所述应用,选取了适合的推杆布局方式。对日后在进行剪叉机构的运动控制、推杆选型与布局上具有一定的借鉴意义。

