钢筋与波纹管连接用灌浆料粘结性能试验研究

李厚荣

(中铁二十四局集团有限公司路桥分公司 上海 200070)

1 引言

随着我国基础设施建设的蓬勃发展，施工环境与安全问题越来越受到业主、设计和施工单位的重视[1]。相比较传统的现浇施工技术，预制拼装桥梁建造技术可在保证施工质量的前提下，更加快速高效、绿色节能、安全可控地建成桥梁[2-4]。预制盖梁、立柱与承台基础之间的连接构造，直接关系到桥梁的施工效率、耐久性、整体受力性能及抗震性能[5-6]。灌浆金属波纹管连接因其工作性能优越、成本经济、施工方便等优势，逐步成为目前工程界中较为常用的预制拼装连接方式。灌浆金属波纹管连接是指将预制墩柱的外露钢筋插入预埋在预制盖梁或承台中的金属波纹管内，并灌注高强灌浆料，形成可靠连接[7]。该连接是通过钢筋与灌浆料之间的粘结来实现力的传递，是保证构件拼装可靠连接的关键[8]。

国内外学者针对钢筋与混凝土之间的粘结滑移问题已开展了大量有价值的研究工作。张伟平等[9]采用外加电流加速钢筋锈蚀的方法，通过钢筋开槽、内贴应变片的方式，开展了半梁式粘结试验，获得了不同锚固长度下的粘结应力分布规律和钢筋混凝土相对滑移的变化规律，建立了综合考虑锚固位置影响的锈后钢筋与混凝土之间的粘结滑移本构关系，推导出了不同锈胀长度状态下，τ-s关系沿着锚固长度方向的变化规律，并提出了能够反映这种变化规律的位置函数。安明喆等[10]采用梁式试验分析了保护层厚度、锚固长度、钢纤维掺量等因素对钢筋与混凝土间的粘结性能影响。陈俊等[11]通过对锈蚀试件和非锈蚀试件开展高温试验和中心拔出试验，研究了高温对锈蚀钢筋混凝土结构粘结锚固性能的影响。郝吉等[12]开展了内贴应变片钢筋的直接拔出试验，综合研究了粉煤灰掺量与冻融循环双重因素对试件粘结性能的影响。通过上述的试验研究，均得出了珍贵的试验数据和宝贵的试验结论，为后续更深入的钢筋与混凝土粘结性能研究及相关类型的试验研究提供了借鉴，也为相关工程的应用提供了积极的指导作用。而关于带肋钢筋与灌浆料间的粘结滑移关系研究尚不多见，且灌浆料是一种特殊类型的混凝土，与普通混凝土的力学性能存在较大差异。为此，有必要进一步开展带肋螺纹钢筋与灌浆料间的粘结滑移关系研究。

为进一步研究带肋螺纹钢筋与灌浆料间的粘结滑移问题，设计并制作了4组8个中心拉拔试件，并基于连续荷载作用下拉拔试验，分析了螺纹钢筋与灌浆料之间的粘结滑移变化规律及粘结应力沿锚固长度方向的分布规律。

2 试验概况

2.1 试件设计与制作

试件的锚固钢筋采用直径d为18 mm、25 mm的HRB400变形钢筋，波纹管外径D为63 mm。参照《混凝土结构试验方法标准》(GB/T 50152-92)的要求，试件尺寸为10d×10d×10d(15d)，锚固钢筋与金属波纹管设置在试件中轴线上，保证严格对中。在钢筋的加载端用长度为5d的塑料套管包裹锚固区钢筋，进行无粘结处理，消除加载装置对试件端部的挤压效应。为防止试件混凝土发生劈裂破坏，在灌浆金属波纹管外围每隔50 mm设置一道横向箍筋。

为探究粘结应力分布沿锚固长度方向上的变化，对钢筋进行开槽处理，槽口尺寸为3 mm×3 mm。沿钢筋锚固长度方向，在两半钢筋槽内粘贴应变片，每隔30 mm粘贴一个，交错布置，钢筋合龙后应变间距为15 mm。合龙时，用环氧树脂密封槽口后将两半钢筋粘贴在一起，并用细铁丝缠绕箍紧，确保两半钢筋粘结可靠。待两半钢筋粘结稳定后，在钢筋的加载端附近，将两半钢筋进行焊接，确保其共同受力。试件的具体形式见图1，试件的设计参数见表1。

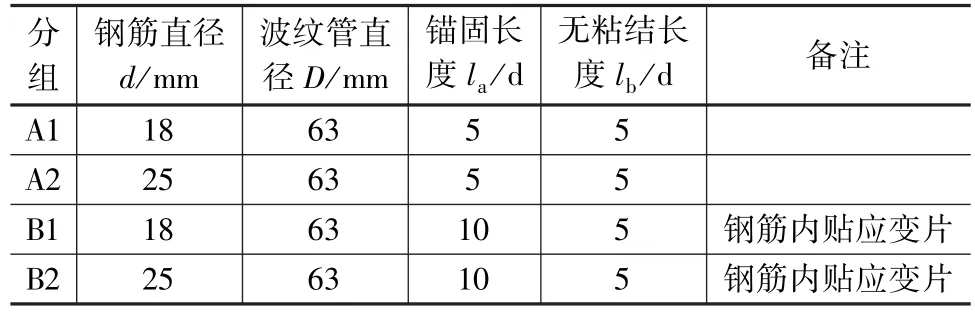
表1 试件主要参数

图1 试件与加载装置示意

2.2 试验材料力学性能

通过拉伸试验，得到钢筋的材料力学性能如表2所示。按照《水泥胶砂强度检验方法》(GB/T 17671-1999)所规定的标准试验方法，检测得金属波纹管灌浆料棱柱体标准试块抗压强度为69.8 MPa，灌浆料立方体劈裂抗拉强度为5.31 MPa。

表2 钢筋力学性能

2.3 试验装置及测量方法

试验采用30 t电液伺服式万能试验机以200～300 N/s的加载速率进行连续加载，直至试件发生破坏为止，试验加载装置见图1。试验过程中，在钢筋的自由端设置1个位移计，取其滑移测量值为自由端滑移量。在钢筋加载端附近设置2个位移计，取其滑移测量均值为测点处滑移量，则钢筋锚固段终点的滑移量为加载端测点滑移值扣除与其之间的钢筋伸长量。拉力由万能试验机测出，并与位移计保持相同的采集频率。加载时，下夹具保持固定，上夹具带动吊笼向上移动。

3 试验结果及分析

3.1 平均粘结应力-滑移量曲线

钢筋与灌浆料间的粘结应力τ可取锚固长度方向上的平均值进行计算，即:

式中，F为外荷载(kN)；la为钢筋锚固长度(mm)；τ为平均粘结应力(MPa)。

A组试件的平均粘结应力-滑移量曲线如图2所示。图2中，s表示钢筋的粘结滑移量。由图2可知，各试件的平均粘结应力-滑移量曲线变化大致相同。试验曲线大致可分为3个部分:上升段、下降段、水平段。钢筋与灌浆料间的粘结力由摩擦力、化学胶着力和机械咬合力共同组成[13]。上升段初期，钢筋与灌浆料间的粘结力主要由化学胶着力和机械咬合力来提供。化学胶着力很小，在较小的荷载作用下就被克服，上升段转由机械咬合力提供。随着荷载的增加，钢筋肋前灌浆料开始被压碎，粘结应力与滑移量之间开始呈非线性变化。当荷载增至极限荷载的70%～80%，肋前灌浆料大面积被压碎，曲线斜率继续减小。当钢筋的自由端达到极限粘结强度时，钢筋与灌浆料之间的咬合齿开始不断被剪断，机械咬合力逐渐退出工作，粘结力开始主要由摩擦力提供。当粘结应力下降至极限粘结强度的55%～65%，粘结应力不再下降，在水平向上下波动变化。由图2还可知，相较A2组，A1组的极限粘结强度更高，表明钢筋与灌浆料之间的极限粘结强度受波纹管与钢筋直径的相对比值影响。当相对比值较大时，钢筋的锚固承载力表现更佳。

图2 平均粘结应力-滑移量曲线

3.2 粘结应力分布曲线

在不同荷载作用下，钢筋沿锚固长度方向上的应变分布如图3所示。图3中，ε为钢筋应变，x表示钢筋锚入深度。由图3可知，钢筋沿锚固长度方向的应变呈不均匀分布，加载端的钢筋应变最大，逐渐向自由端减小。锚固区中间段的应变变化较为显著，且增长呈加快趋势，两端的应变变化趋于平缓。随着荷载的增大，锚固长度范围内的钢筋应变逐渐增大，但各曲线都呈现出基本一致的变化规律。根据钢筋的应变分布，可获取钢筋与灌浆料间的粘结应力沿锚固长度方向上的变化[14]。粘结应力沿锚固长度方向上的分布如图4所示。由图4可知，不同荷载作用下的粘结应力分布曲线变化规律是基本吻合的，钢筋的自由端和加载端的粘结应力均趋于零，而在距离加载端0.2～0.3倍钢筋锚固长度处，粘结应力取得最大值。加载初期，粘结应力主要分布在加载端附近，靠近自由端区域粘结应力为零。随着荷载的增大，力逐渐传递至自由端。对比B1和B2两组试验曲线可知，其变化规律存在一定差异性。相较B2组，B1组试件沿锚固长度方向上的粘结应力分布更为均匀，可能是受钢筋直径的影响。以上表明，当锚固长度较大时，应考虑钢筋与灌浆料间粘结应力分布变化的影响。

图3 钢筋应变分布曲线

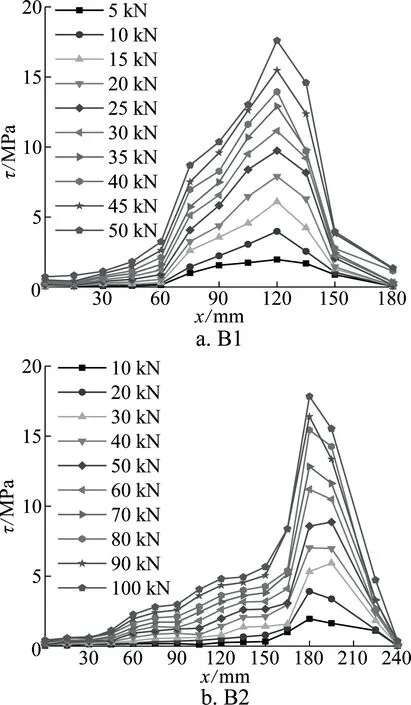
图4 粘结应力分布曲线

4 钢筋锚固长度建议取值

类型Ⅰ:根据《混凝土结构设计规范》(GB 50010-2010)第8.3节可知，受拉钢筋锚固长度la按式(2)和(3)计算:

式中，各参数根据试验结果和规范取值；la取值应≥200 mm；ξa取值1.25；α取值0.14；fy分别取值610 MPa和603 MPa；ft取值5.31 MPa；d为钢筋的标准直径(mm)。

类型Ⅱ:根据美国混凝土结构建筑规范和注释ACI 318 M-05的12.2条规定，19号钢筋(直径19.05 mm)及以下和22号钢筋(直径22.23 mm)以上的锚固长度ld分别按式(4)和(5)计算:

式中，各参数根据试验结果和规范取值；fy分别取值437 MPa和422 MPa；f′c取值69.8 MPa；ψt为顶部钢筋对浇筑位置的不利影响系数，取值1.0；ψe为环氧涂层的影响系数，取值1.0；λ为混凝土品种系数，取值1.0；db为钢筋的标准直径(mm)。

类型Ⅲ:根据《钢筋套筒灌浆连接应用技术规程》(JTG 355-2015)，取钢筋与灌浆料达到极限粘结强度时，钢筋刚好拉断的状态为破坏临界状态。钢筋的锚固力为，拉断承载力为Fu＝fu·πd2/4，由此可得临界状态方程为:

式中，各参数根据试验结果和规范取值；fu为钢筋极限抗拉强度，分别取值610 MPa和603 MPa；τu为极限粘结强度，分别取值23.2 MPa和21.5 MPa；为钢筋拉断临界锚固长度(mm)；d为钢筋的标准直径(mm)。

依据上述三种类型和规范计算，可得18 mm和25 mm钢筋锚固长度如表3所示。由表3可知，相较类型Ⅲ，类型Ⅰ和类型Ⅱ所规定的锚固长度偏于保守，表明在波纹管约束下的钢筋锚固长度大大减小。基于安全，考虑1.5～2.0倍的安全系数，实际使用当中，钢筋锚固长度建议取值10～15d。

表3 钢筋锚固长度计算值

5 结束语

基于4组中心拉拔试件在连续荷载作用下的拉拔试验，分析了螺纹钢筋与灌浆料间的粘结滑移变化规律及粘结应力沿锚固长度方向的分布规律，并主要得出以下结论:

(1)典型的粘结应力-滑移量曲线可由上升段、下降段和水平波动段三部分组成。

(2)螺纹钢筋与灌浆料间的极限粘结强度受波纹管与钢筋的相对直径比值的影响，当相对比值较大时，极限粘结强度更大，锚固性能表现更佳。

(3)当锚固长度较大时，钢筋与灌浆料间的粘结应力沿锚固长度方向呈不均匀分布，在距离加载端0.2～0.3倍钢筋锚固长度处，粘结应力取得峰值，且当波纹管与钢筋的相对直径比值较大时，粘结应力分布相对趋向更均匀。

(4)实际使用当中，当钢筋直径≤25 mm时，螺纹钢筋的高强灌浆锚固长度建议取值为10～15倍钢筋直径。