基于塑性变形理论的圆形抗滑桩边坡稳定性分析

周记名

(中国土木工程集团有限公司 北京 100038)

1 引言

圆形抗滑桩因其结构形式简单、机械成孔速度快、理论计算原理成熟、抗滑能力强等众多优点，在地质灾害抢险工程中广泛地应用[1-4]。近几十年来，圆形抗滑桩在边坡加固中的施工工艺和滑坡的治理实践上取得了长足得发展[5]，但由于目前对滑坡机理理论分析尚未达到成熟的地步，由此发展出了众多的理论计算方法，并没有形成一个统一的定论。1970年，Matlock等提出了p-y曲线法计算桩的水平承载力[6]，同时考虑了土的非线性条件；1975年，Tomio等考虑了桩土之间的相互作用，桩在受力变形时，桩间土形成土拱效应，并参与受力计算，提出了Ito塑性变形理论[7]；1998年，Wang和Reese采用弹性地基梁理论建立了抗滑桩的挠曲微分方程，Poulos在此基础上利用有限差分法推导了公式的初步解[8]；2006年，夏永成在Ito塑性变形理论的基础上，推导出了临界桩间距公式[9]；2018年，杨傲分析了桩间土-拱的形成机理，并提出了拱厚度的计算公式，得出土拱截面强度的验算方法和抗滑桩间距的上下限值[10]。尽管如此，由于桩在受荷变形时，桩土相互作用机理的复杂性，且Ito塑性变形理论在理论模型建立时做了众多假设，导致计算不尽合理[11-12]，本文尝试基于Ito塑性变形理论，计算中考虑桩土相互作用产生的摩擦力，从而推导出圆形截面抗滑桩在考虑土-拱效应同时计入桩土摩擦力的水平分布力计算公式，通过推导的公式对边坡稳定性进行求解，同时，结合工程算例，讨论边坡土体重度γ、黏聚力c、内摩擦角φ和桩间距D对边坡稳定性的影响。

2 塑性变形理论基本原理

1975年，Tomio Ito在研究黏土中的桩基水平承载力时，利用极限平衡力理论，提出了Ito塑性变形理论，该理论考虑了土体由于桩的阻挡形成的土拱效应，如图1所示，假设存在一排抗滑桩，桩径为D，桩中心距为D1，桩净间距为D2，土体通过变形左右将荷载传递到抗滑桩上，抗滑桩的应力发生调整，形成AEBB′E′A′应力重分布区域，并作出以下理想假设[13]:

(1)由于土体滑动变形，桩间土形成了滑动面AEB和A′E′B′；

(2)AEBB′E′A′区域中的土体达到塑性屈服状态，采用Mohr-Coulomb本构关系；

(3)将该模型简化为二维模型以便于进行受力分析；

(4)抗滑桩简化为刚性体；

(5)滑动面AA′的应力边界条件为主动土压力；

(6)计算分析时忽略滑动面AEB和A′E′B′上的摩擦力。

通过假设模型条件可以得出单位厚度土体作用在圆形截面抗滑桩上的水平分布力:

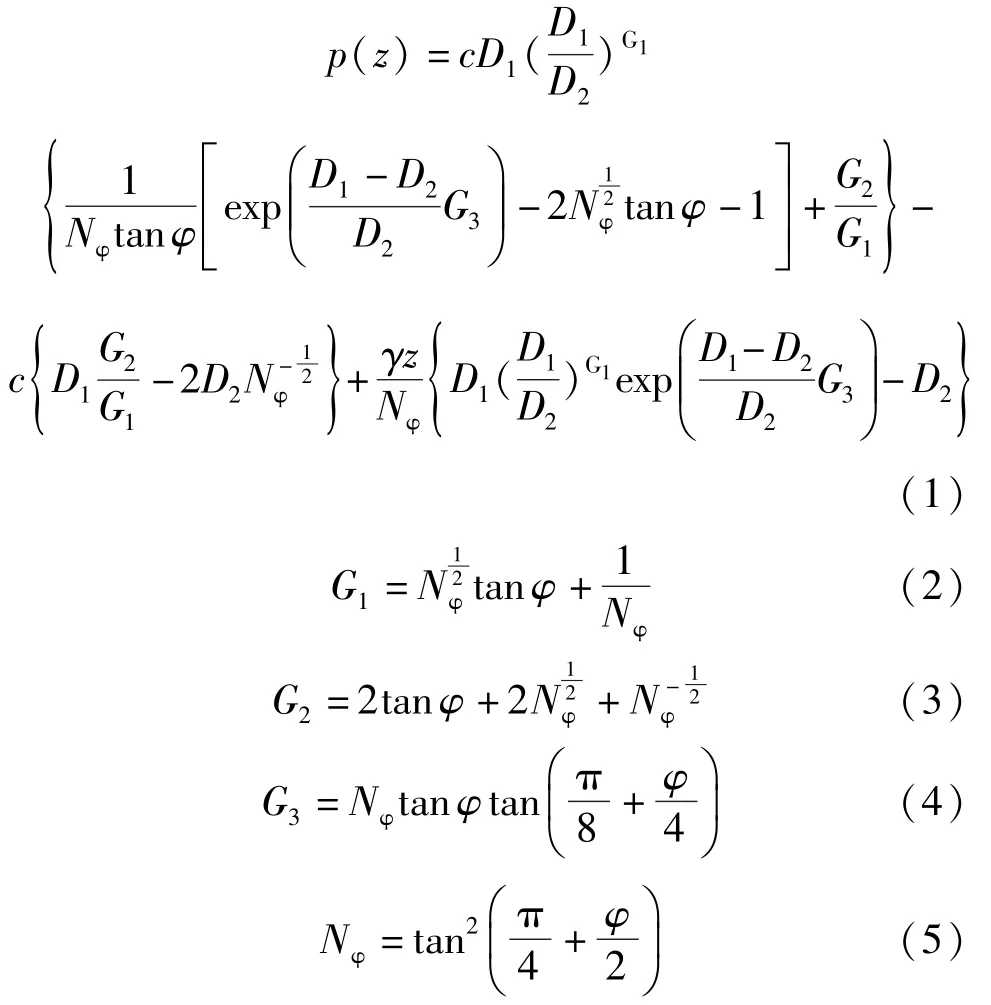
式中，D1为圆形截面抗滑桩中心距；D2为圆形截面抗滑桩净间距；c为土的黏聚力；φ为土的内摩擦角。

3 圆形截面抗滑桩水平分布力推导及边坡稳定性计算

3.1 圆形抗滑桩水平分布力推导

由于Tomio Ito塑性变形理论分析时忽略了滑动面AEB和A′E′B′上的摩擦力，该理论不够严谨，从而导致计算结果不甚合理。基于Tomio Ito塑性变形理论对圆形抗滑桩水平分布力的计算公式推导如下。

在区域EBB′E′取土体单元，如图2所示，可得力学平衡微分方程如下:

土体屈服准则:

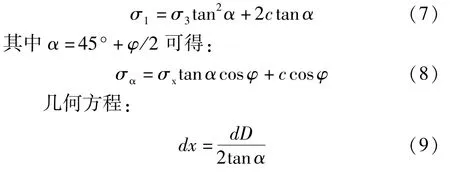
将式(8)、(9)代入式(6)并积分可得:

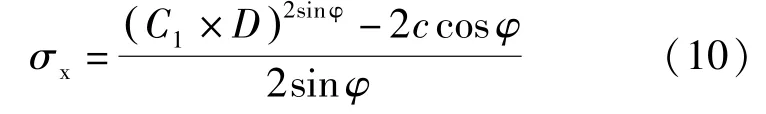
式中，C1为积分常数。

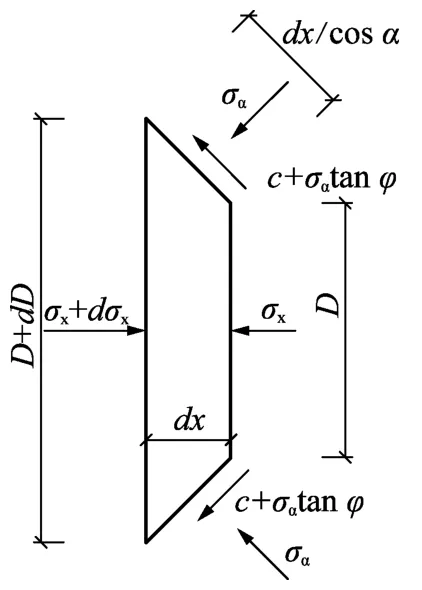
图2 EBB′E′取土体微元

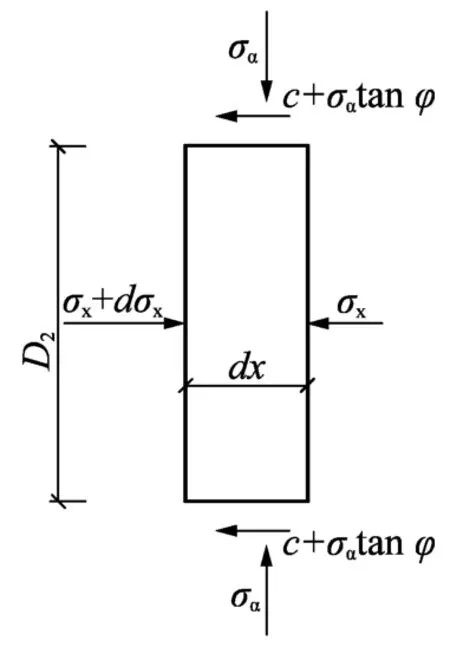
图3 AEE′A′土体单元

类似地，在区域AEE′A′取土体单元，如图3所示，可得力学平衡微分方程如下:

式中，C2为积分常数。

积分常数C1和C2的求解，对方程(10)和方程(11)设置应力边界条件，取抗滑桩任意截面深度z，采用AA′上边界应力作为土的主动土压力:

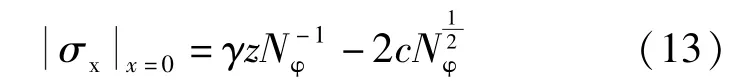
可求得C2:

将方程(14)代入方程(12)，再代入方程(10)可求得C1:

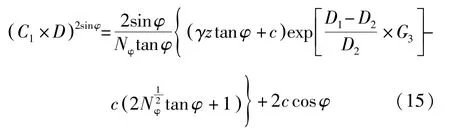
由方程(15)和方程(10)可知在BB′面上的抗滑桩水平力分布力:

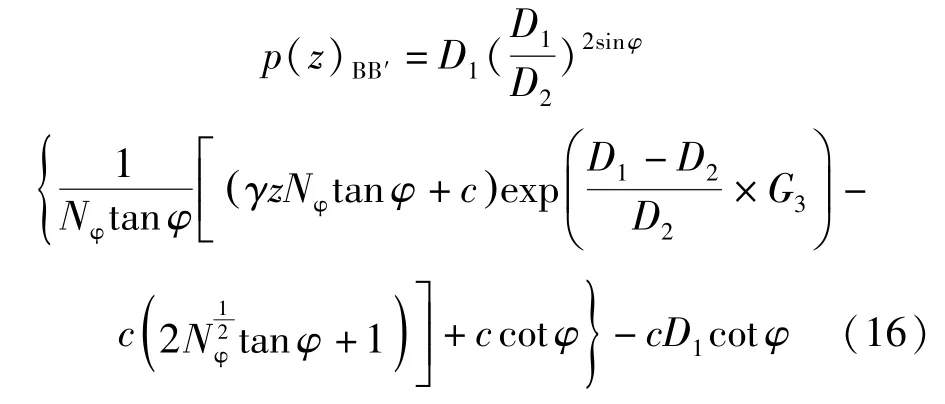
BB′面上的水平力分布力与A A′上水平应力即为作用在抗滑桩上的侧向分布力，由此可得:

3.2 边坡稳定性计算

由方程(17)沿桩身范围进行积分，即可计算出抗滑桩所受边坡的总水平力，由此可以计算出每延米的边坡水平力(P)和相应的作用点(Z0):

桩身抗力与方程(18)计算值之比即为边坡的稳定性系数Fs。

4 工程算例

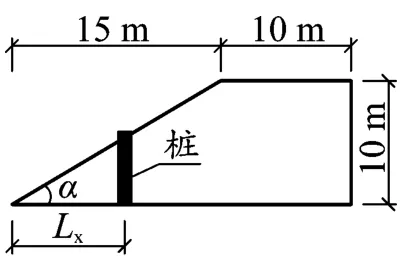
图4 边坡算例模型

假设某Ⅲ级边坡概况如图4所示，仅考虑一般工况(Fs＝1.25为稳定条件)，假设坡高H＝10 m，坡顶宽L1＝10 m，坡肩至坡脚的水平距离L＝15 m，设置一排抗滑桩于坡面上，抗滑桩桩径d＝1.0 m，桩间距S＝2.0 m，桩顶为自由状态，抗滑桩与坡脚的水平距离为Lx。坡体的重度为γ＝22 kN/m3，黏聚力c＝10 kPa，内摩擦角φ＝22°，土体弹性模量Es1＝20 MPa，土体的泊松比μ1＝0.25，抗滑桩的重度为γ1＝25 kN/m3，桩体弹性模量Es2＝30 000 MPa，抗滑桩泊松比μ2＝0.30。

根据第3章的推导公式，计算结果如图5所示。从图5中可以得出抗滑桩位置的设置对边坡稳定性和桩身抗力产生明显影响，边坡稳定性系数随着桩身距离坡脚距离的增加，呈倒抛物线的变化趋势，当桩身距离坡脚为7 m(0.5L)时边坡稳定性达到最大，6 m(0.4L)～9 m(0.6L)时满足边坡稳定性要求，达到理想状态；滑坡推力和桩身抵抗力的曲线变化趋势一致，满足作用力与反作用力的相互关系，滑坡推力和桩身抗滑力随着抗滑桩与坡脚距离的增大而增大，最后在距离为10 m(0.67L)～12 m(0.8L)左右出现最大值，随后出现急剧下降的变化趋势。

图5 边坡稳定性计算曲线

从方程(17)可以看出，土体的重度、内摩擦角和黏聚力及桩间距都对桩的水平分布力具有一定的影响，进而影响边坡的稳定性。为了考察这些影响因子的影响程度，分别设置不同的参数值进行计算，计算结果如图6～图9所示。从图6可以看出，边坡的稳定性随着土体重度的增加有所提高，但效果不明显，当Lx＝7 m的时候边坡稳定性系数达到峰值；当Lx＜7 m的时候，边坡稳定性系数随着土体容重的增加而提高；当Lx＞7 m时，边坡稳定性系数随着土体容重的增加而降低；数据表明当桩身距坡脚水平距离Lx＞0.5L时，土体重度的增加对边坡稳定性的影响效果更加明显。从图7和图8可以看出，边坡稳定性系数随着边坡土体黏聚力(c)和内摩擦角(φ)的增大有着较为显著的增加趋势。由图9可以看出，边坡稳定性系数随着桩间距(D)的增加出现下降趋势，桩间距D＝2 m和D＝2.5 m的时候，边坡稳定性系数比较接近，没有显著的变化，当D＝3 m时，边坡稳定性系数出现了较大的降幅，建议在桩间距布置的时候，综合考虑边坡安全系数和工程造价的情况下，采取2～2.5倍桩径进行布桩是合理的。

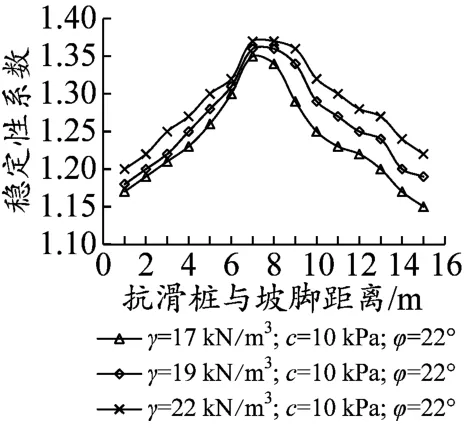
图6 土体容重与边坡稳定性系数变化曲线

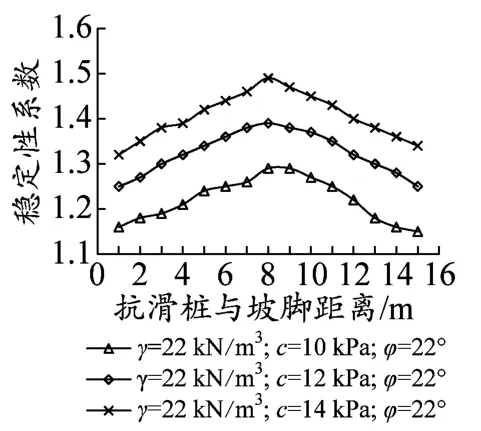
图7 土体黏聚力与边坡稳定性系数变化曲线

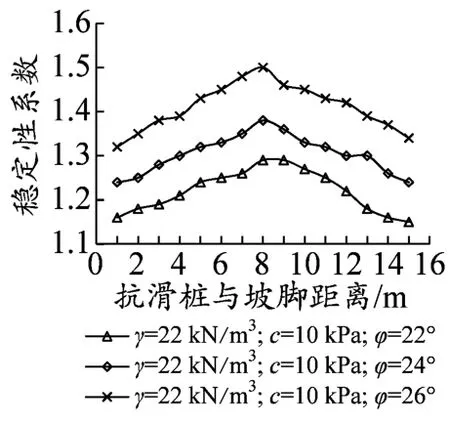
图8 土体内摩擦角与边坡稳定性系数变化曲线

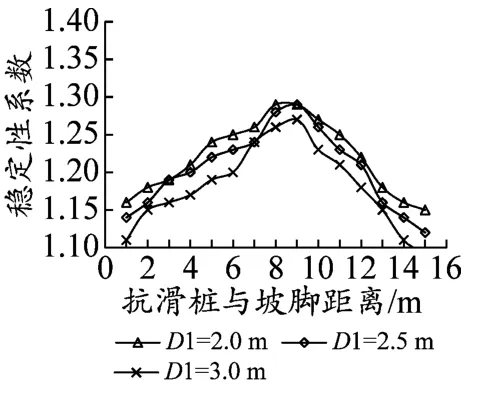
图9 桩间距与边坡稳定性系数变化曲线

5 结论

(1)基于Ito塑性变形理论，推导出考虑桩-土相互作用的土-拱效应作用下，计入桩-土摩擦力的圆形截面抗滑桩水平分布力计算公式如方程(17)以及边坡稳定性系数Fs。

(2)结合工程算例，得出圆形截面抗滑桩的布设位置对桩身抗力和边坡稳定性系数的影响。边坡稳定性系数随着桩身距离坡脚距离的增加，呈倒抛物线的变化趋势，在桩身距离坡脚约为0.5L时边坡稳定性系数达到最大值，当桩身距离坡脚为0.4～0.6L时满足边坡稳定性要求，达到理想稳定状态，为边坡工程中合理布置圆形抗滑桩位置提供参考依据。

(3)土体容重(γ)、内摩擦角(φ)、黏聚力(c)的增加可提高边坡的稳定性，其中黏聚力(c)和内摩擦角(φ)起到主要影响因素；当桩身距坡脚水平距离＞0.5L时，土体重度的增加对边坡稳定性的影响效果更加明显；在考虑边坡稳定性和工程造价的因素时，建议采用2～2.5倍桩径的距离进行合理布桩。