影响加筋土挡墙墙背水平土压力的参数分析

王 宁 李远洋 刘嘉良 王志猛 蒋关鲁

(1.西南交通大学土木工程学院 四川成都 610031；2.中国中铁二院工程集团有限责任公司 四川成都 610031)

1 引言

近年来，随着加筋土挡墙的兴起，其结构形式在多个领域得到了广泛的应用，针对加筋土挡墙的研究也越来越多，加筋土挡墙的受力机理、破坏模式及设计方法也激发了众多学者的兴趣。加筋土挡墙墙背水平土压力的分布是挡墙配筋计算及整体稳定性计算的重要参考依据，也是了解加筋土挡墙加筋效果工作机理的重要途径。

目前，对于墙背土压力的常见计算方法有:正应力梯形分布法、Osman能量法、库仑力矩法、库仑合力法[1]、正应力均匀分布法、正应力梅氏分布法、经验法和公路变系数法等。这些方法大多基于极限平衡理论，而加筋土挡墙在实际工作状态下并没有达到极限状态。因此，上述理论并不能很好地解释加筋土挡墙墙背水平土压力的实际分布情况。杨广庆等[2]以赣(州)龙(岩)铁路整体现浇面板式加筋土高挡墙为工程依托开展现场试验，实测墙背侧向土压力沿墙高呈非线性形式分布。王贺等[3]通过室内模型试验，发现墙内水平土压力在不同位置沿墙高分布有所不同。唐辉明等[4]在三峡库区高57 m的超高加筋土挡墙的研究中采用离心模拟技术，发现加筋土挡墙墙背土压力随墙高呈两头小、中间大的分布规律，并非沿着墙高从顶到底线性增大。陈建峰等[5]针对软土地基反包式土工格栅加筋黏性土挡墙，开展了现场测试，通过对挡墙在填筑过程进行受力分析发现，在挡墙破裂面形成后，墙背水平土压力和挡墙体内垂直土压力分布不再增大。

综上所述，墙背水平土压力沿墙高呈现非线性分布，最大水平土压力位于墙体中间偏下位置。本文将结合离心机模型试验水平土压力实测结果和数值模拟结果进行对比分析，验证其可行性，并在此基础上对填料摩擦角、连接件长度及筋材刚度等因素加以考虑，探讨这些因素对加筋土挡墙墙背水平土压力的影响。

2 试验方案

2.1 试验概况

离心机模型试验原型尺寸及力学参数与数值模拟模型相一致。模型箱试验相似比采用1∶50，土工格栅采用宽度为4 mm，厚度为0.12 mm的磷青铜带编织而成，纵向间隔为30 mm，横向间隔为80 mm；整体现浇式混凝土面板采用铝制面板代替；连接锚杆及锚板分别根据抗拉强度相似原则以及抗弯刚度相似原则采用铜带(实测极限抗拉强度500 MPa，间距3 cm)及木板进行模拟。

2.2 仪器布置

试验主要测试墙背土压力和构件应变。分别在不同位置布置若干水平土压力盒、竖向土压力盒及应变片。具体布置方式为:墙背布置4个水平土压力盒；自下而上分别在第1层、第4层和第5层布置3个竖向土压力盒；自下而上在第1、2、4、5层格栅上分别布置4个应变片，同时在各层的连接件上粘贴应变片[6-7]，如图1所示。

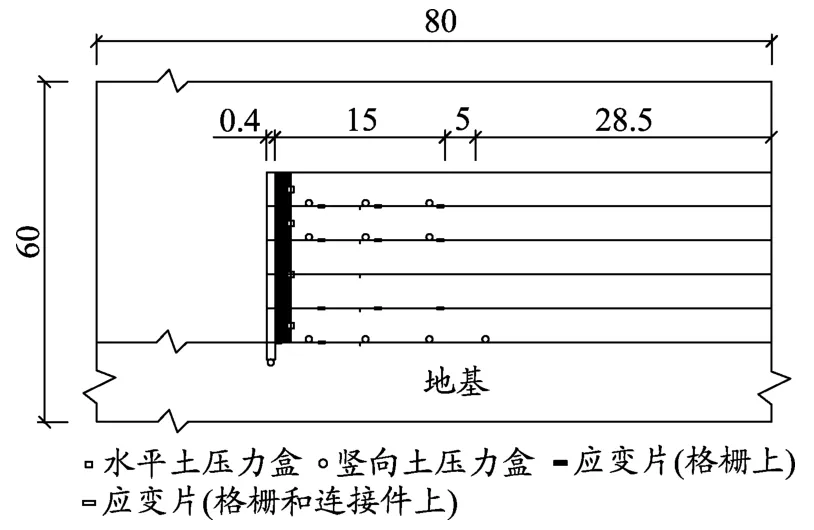
图1 仪器布置(单位：cm)

3 有限元建模

FLAC3D具有解决复杂力学问题的强大能力，可以根据实际情况选用相应的材料模型，从而较为合理地反映实际情况下结构的受力特性。现主要应用于岩土体的渐进破坏和崩塌现象、岩土体材料变形局部剪切带的演化模拟及岩土体动力稳定性、土体与结构的相互作用及液化现象等方面的研究。

3.1 材料本构及参数

模型由地基、填料、土工格栅、连接件、面板构成，可分别由FLAC3D中的实体单元与结构单元进行模拟[8]，如图2所示。

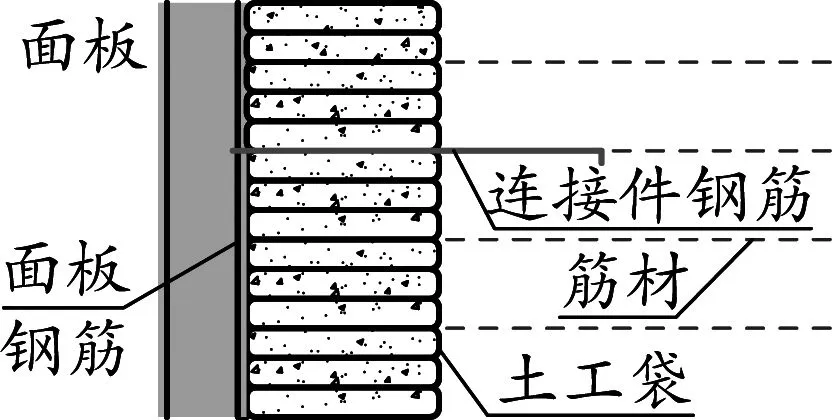
图2 加筋体结构

加筋土挡墙墙体与混凝土面板之间通过预埋锚固钢筋(连接件)连接在一起，钢筋其余部分伸入土体内部，协同加筋体共同受力[9]，具体见图2。

(1)填料

填料模型采用传统的Mohr-Coulomb模型，其中填料摩擦角取为35°，重度为23 kN/m3。

FLAC3D数值模拟中对于Mohr-Coulomb模型，需要指定填土的弹性参数。对于弹性模量通常可采用下式表示:

式中，E代表数值模拟中采用的弹性模量值；Es为填料的压缩模量。

(2)土工格栅

土工格栅采用geogrid结构单元模拟，其可以抵抗薄膜荷载但不能抵抗弯曲荷载。对于伸长率为2%，拉力为37 kN/m的土工格栅，geogrid结构单元的弹性模量设置为9.25×108Pa，筋材与填土之间的界面角度取为填土摩擦角。

(3)面板

面板采用实体单元模拟，选用弹性模型。面板尺寸为:宽0.3 m，高7.5 m。

(4)接触面

FLAC3D数值模拟中接触面的法向刚度kn和切向刚度ks值通常设置为10倍周边单元体最硬相邻区域的等效刚度，可用下式表示:

式中，K为体积模接触单元体法向最小宽度。

(5)模型参数取值及模型

模型具体参数取值见表1。

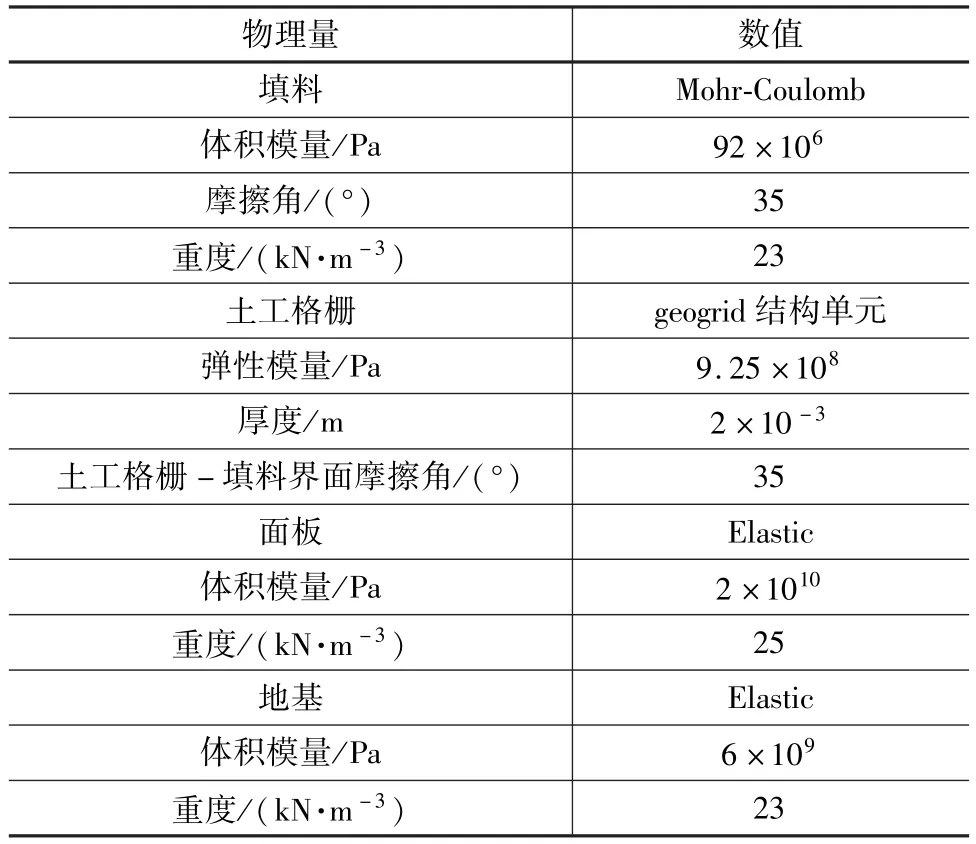
表1 Flac数值模拟原型材料参数

3.2 模拟与实测结果对比

数值模拟结果和离心机模型试验结果对比如图3所示。

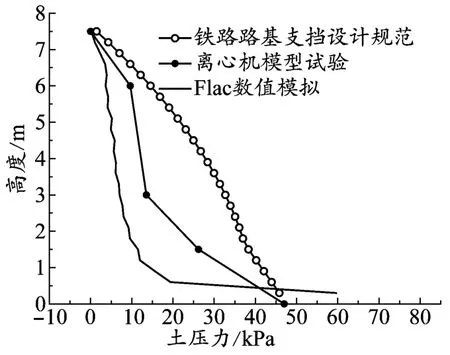
图3 土压力分布

(1)数值模拟值和实测值较为接近，且土压力分布规律一致[10-11]，说明采用的数值模型可行，可以用此方法进行墙背水平土压力的分析。

(2)墙背水平土压力数值模拟值和实测值均明显低于规范计算值，在沿墙高的分布规律上存在一定的差异。

4 参数分析

4.1 铁路路基支挡规范计算

根据《铁路路基支挡结构设计规范》[12]，作用于路肩挡土墙墙面板上的水平土压应力应按下列公式计算:

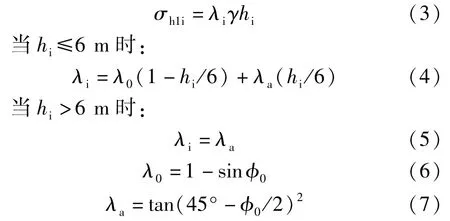
式中，σh1i为墙背填料水平土压力；λi为加筋土体内深度hi处土压力系数；γ为填料重度；φ0为填料综合内摩擦角；hi为墙顶距第i层墙面板中心的高度；λ0为静止土压力系数；λa为主动土压力系数。

为了研究不同设计参数时加筋土挡墙的受力及变形特性，总共进行表2所示工况的对比。

表2 Flac数值模拟原型材料参数

4.2 筋材竖向间距对土压力的影响

依次取有无连接件及土工格栅竖向加筋间距不同(0.3、0.9 m)进行对比，结果如图4所示；墙面位移如图5所示。

图4 墙背水平土压力(竖向间距不同)

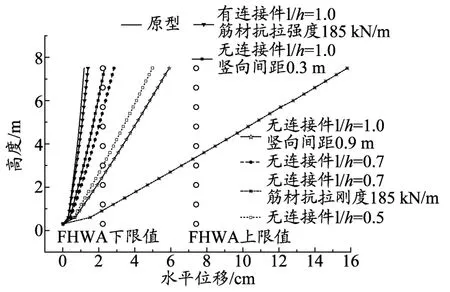
图5 墙面位移

图4表明:与原型相比，没有连接件时墙背水平土压力明显增大；当去掉连接件并且竖向间距增大时，墙背水平土压力增幅较明显。导致上述现象产生的原因为:连接件添加后，协同面板共同受力，能够承担一部分拉力，从而使面板承受的土压力减小。

由图4可知，连接件的使用，可以有效减小墙背水平土压力。数值模拟值与设计规范计算值相比，相对较小。顶部差值很小，随着高度的降低，差距逐渐变大，一方面是因为朗肯土压力理论的假设前提(墙背垂直、光滑、整体平移)与加筋土挡墙实际情况(具有一定坡度、柔性面板、加筋作用)不符；另一方面是因为挡墙墙背与土体间的摩擦、筋材对土体的水平限制作用以及墙面的水平位移等均能导致墙背水平土压力的减小。从墙面水平位移图5可以发现，由于墙体底部位移较墙顶面较小，故而墙底水平土压力较大，且存在应力集中现象。随着筋材间距的增大，墙面位移呈现增大趋势。当去掉原型中的连接件时，墙顶位移大于FHWA规定的下限值2.2 cm；当继续增大格栅竖向间距时，2/3墙高范围内的位移值超过规范下限值，并且墙顶处的位移接近规范的上限值7.4 cm。上述现象说明:连接件的存在是非常必要的，不可忽略；筋材竖向间距对墙背水平土压力也有一定影响，在设计时要注意选取适当的筋材间距。

4.3 格栅长度对土压力的影响

土工格栅加筋长度依次取为7.5、5.25、3.75 m，对比计算结果如图6所示。

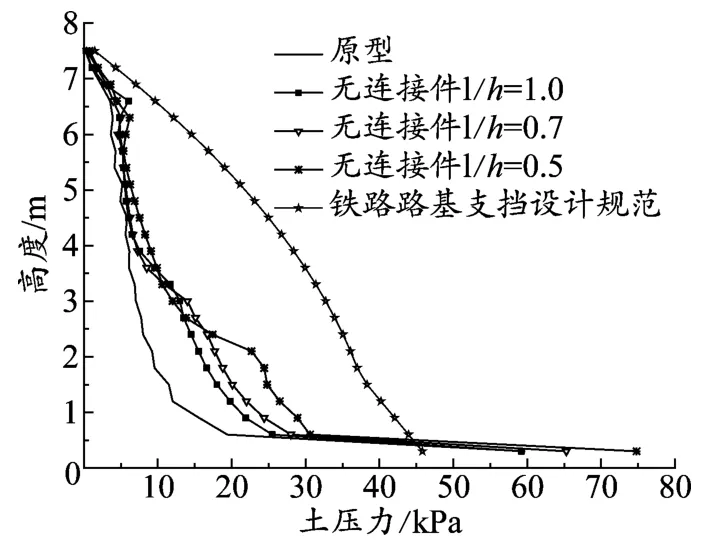
图6 墙背水平土压力(格栅长度不同)

图6表明，加筋材料长度的减小将导致墙背水平土压力的增大，特别是中下部，其增幅相对更加明显。这是由于土体与筋材相互作用与共同受力的情况下，加筋土作为一种复合材料形成了自己的力学性质。筋材长度的增加，实际上是增大了填料的刚度和整体性，加筋体的承受能力增强，摩阻力约束了土体的侧向变形，减小了墙背水平土压力。格栅长度变化时，图5墙面位移的变化趋势与上文呈现一致的趋势，且均未超过限值。综合两图可以看出，当无连接件且格栅长度为7.5 m和5.25 m时，墙背水平土压力和墙面板位移均差距不大，而当格栅长度减小为3.75 m时，两者均变化明显，因此在设计使用中应保证合适的土工格栅加筋长度。

4.4 格栅刚度对土压力的影响

依次取土工格栅加筋刚度为185、1 850 kN/m，对比计算结果如图7所示。

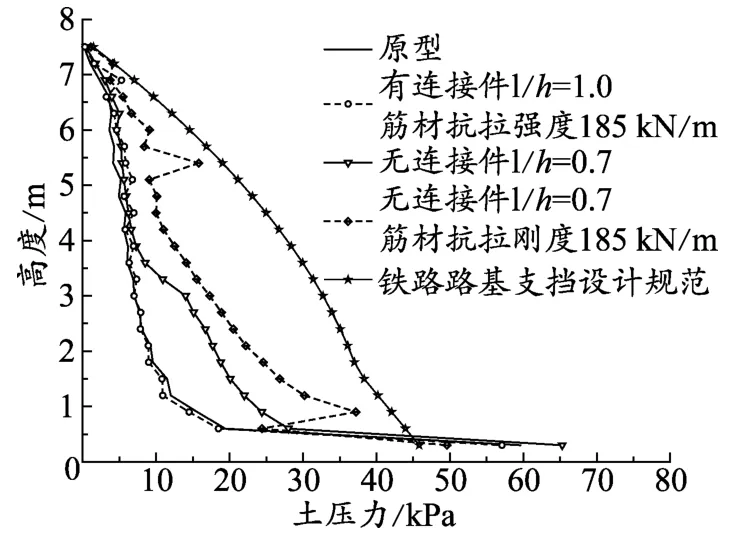
图7 墙背水平土压力(格栅刚度不同)

由图7可知，当连接件存在且格栅长度较长时，格栅抗拉强度对墙背水平土压力影响不大；当无连接件时，随着土工格栅刚度的增大，墙背水平土压力减小；当格栅抗拉强度减低幅度较大时，墙背水平土压力增大量也较大。分析其原因，当格栅参数均较大且连接件存在时，加筋体整体刚度较大，格栅一部分强度得不到发挥，降低格栅刚度后对整体影响不大。当无连接件且格栅参数较小时，加筋体整体刚度较小，格栅刚度对整体影响较大。从墙面位移图5可知，当无连接件且格栅参数较小时，墙面位移较大，大于FHWA上限值。综合两图，应采用合理的土工格栅设计参数组合，从而减小挡墙面板处的水平土压力及墙面板位移，提高挡墙的整体稳定性。

4.5 综合对比

如图8所示:原型情况下，墙背水平土压力显著减小；在同样没有连接件的情况下，筋材抗拉刚度减小10倍时，墙背水平土压力增幅明显。总之，筋材对墙背水平土压力的影响主要集中在墙背高度的中下部，且连接件及筋材模量对墙背水平土压力的影响最大。

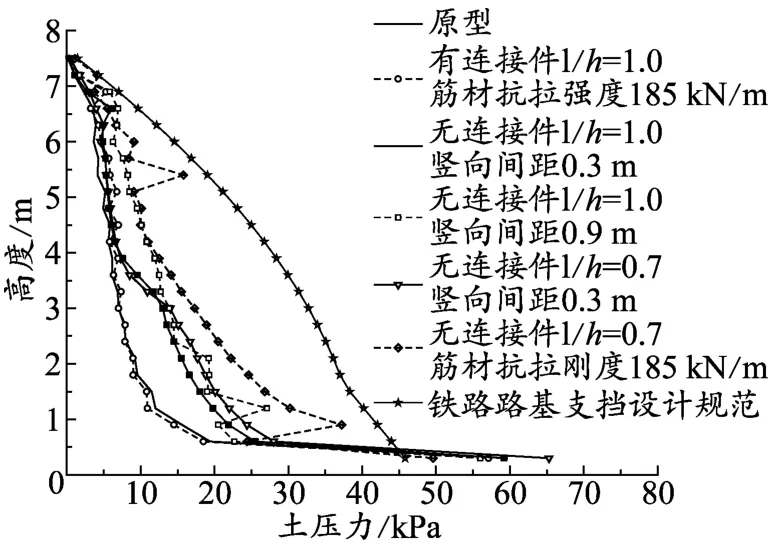
图8 墙背水平土压力(综合)

由于在建模时设定挡墙面板底部和基础为接触面连接，面板向外倾的幅度相对较小，墙背土压力衰减不明显；在面板的中上部，面板侧向位移相比下端较大，墙背水平土压力得到释放，衰减较快，顶部土压力最小。

总的来看，墙背水平土压力沿墙高呈非线性分布，上部较小，接近底部剧增(挡墙底部的面板水平土压力剧增与该处面板的变形受基础顶的限制有关)，非线性分布可能是墙体内水平土压力和筋材与土体的摩擦力共同作用的结果。

5 结论

(1)墙背水平土压力沿墙高呈曲线型分布。理论计算出的水平土压力值与数值模拟相比均差异较大；在大部分的墙高范围内，均大于模拟值较多。

(2)加筋土挡墙墙背水平土压力分布规律反映出:筋材、填土等参数对面板中下部的水平土压力影响较大，筋材长度的提高及间距的减小可有效降低墙背水平土压力。

(3)连接件的存在可以减小墙背水平土压力，在设计时不应忽略。

(4)采用合理的土工格栅设计参数组合，可以有效减小挡墙面板处的水平土压力及墙面板位移，提高挡墙的整体稳定性。