端撑对变电站构架柱计算长度的影响研究

郭 浩

(福建省建筑科学研究院有限责任公司，福建 福州 350028)

0 前 言

为确保变电站构架的整体稳定，通常可在构架柱边设置端撑，根据现有研究结果[1-3]表明端撑的存在能够有效减低柱底内力和变形，从而提高构架的整体刚度。根据现有的变电站构架形式，存在连续两跨及以上构架梁高度不同以及柱中设置端撑的情况，而现有的设计手册[4-5]并未给出该类构架柱的计算长度系数。

本文研究连续架梁高度不同以及柱中布置端撑对构架柱计算长度的影响，利用MIDAS GEN软件建立有限元模型，对其进行屈曲分析，得到该类构架柱的计算长度系数，为变电站构架的设计提供参考价值。

1 模型概况

1)几何尺寸。为了研究连续跨构架梁高度不同以及柱中设置端撑杆件时对构架柱计算长度的影响，本文考虑了三种构架形式，如图1所示。在三种构架中，构架柱选用钢筋混凝土环形柱，柱的外径为300 mm、壁厚为50 mm；横梁选用外径为100 mm的圆钢，材质为Q235碳素钢；端撑柱选用钢管外径为150 mm、壁厚为5 mm的圆钢管，材质为Q235碳素钢。

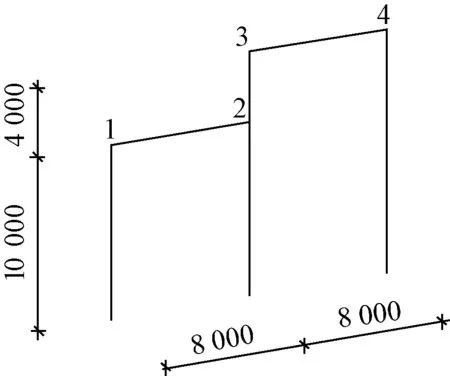
(a)模型a

2)边界条件。在有限元模型中，构架柱、端撑与地面的连接方式选择一般支撑，其中，构架柱与地面间的节点约束整体坐标系中X、Y、Z三个方向的位移和转角(Ux、Uy、Uz、Rx、Ry、Rz)，端撑与地面间的节点约束整体坐标系中X、Y、Z三个方向的位移(Ux、Uy、Uz)；端撑和构架柱间选用铰接，钢梁两端释放除沿杆件轴线方向外的梁端弯矩。

3)荷载施加。在静力荷载工况中添加恒荷载，初始荷载设为1 N，临界荷载(Pcr)就是初始荷载与临界荷载系数(由屈曲分析得到的特征值)的乘积，表示结构构件在临界荷载作用下会发生屈曲失稳；初始荷载统一施加在各构架模型中柱的顶点位置处，同时，为了提高计算精度，需对构架柱进行分段。

2 数值分析

2.1 屈曲向量

利用有限元软件MIDAS GEN建立三种构架的有限元模型，并进行屈曲分析，得到各模型中柱在压力作用下的屈曲向量，如表1所示(表1中的节点号见图1)。

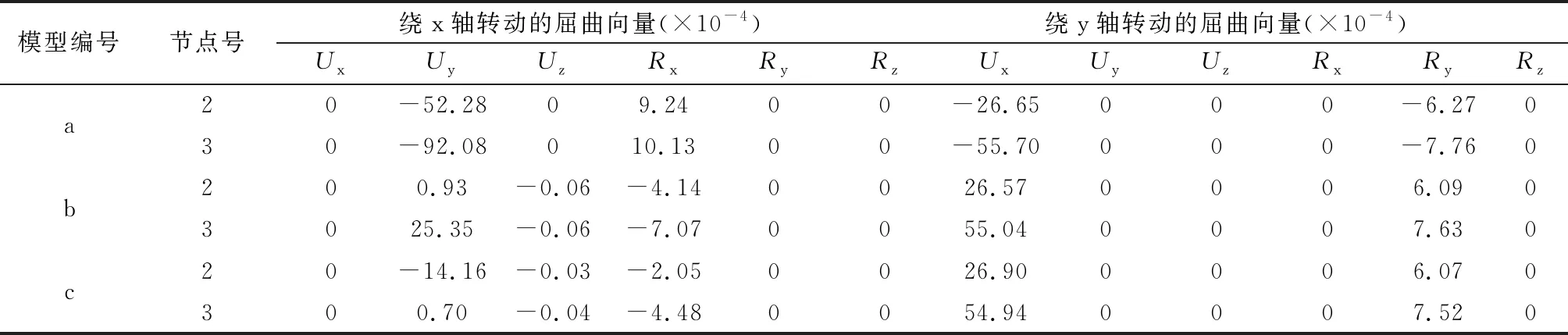
表1 构架中柱绕x轴转动时的屈曲向量

当模型绕x轴转动时，模型b和模型c的屈曲向量比模型a的屈曲向量小，模型b在2号节点处的屈曲向量以及构架c在3号节点处的屈曲向量减小显著；当模型绕y轴转动时，三种模型在各点处的位移向量和转角向量较接近。

2.2 屈曲模态

当初始荷载施加在构架中柱顶部时，三种模型在绕x轴转动、绕y轴转动作用下的屈曲模态如图2所示。图2显示，当模型绕x轴转动，模型a、模型b、模型c的结果最大值为9.21×10-3、2.54×10-3、1.59×10-3，说明端撑的存在有效约束了构架的变形，其中模型三的变形幅度最小；当模型绕y轴转动时，模型a、模型b、模型c的结果最大值为5.57×10-3、5.50×10-3、5.49×10-3，计算结果较接近。

(a)模型a(绕x轴转动)

3 构架柱计算长度分析

3.1 欧拉公式

根据压杆稳定理论可知，在压力作用下，杆件承受的荷载增加到某个限度时，受压杆件将由稳定状态转化为不稳定状态，这个荷载的限值称为临界压力(Pcr)，临界压力是受压杆件保持直线稳定形状时所能承受的最小压力[6]。通过屈曲分析可得到各柱的临界压力，最后通过欧拉公式得到结构构件的计算长度，欧拉公式的通用形式如式(1)所示：

(1)

式中，E为构架柱的弹性模量；I为构架柱的截面惯性矩；μ为计算长度系数；l为柱的长度，mm。

3.2 计算长度分析结果

通过对三种构架模型进行屈曲分析得到各模型的临界压力，现选择三种模型的中柱作为研究对象，利用欧拉公式可求得各模型中柱沿x轴转动、沿y轴转动时的计算长度系数，如表2所示。

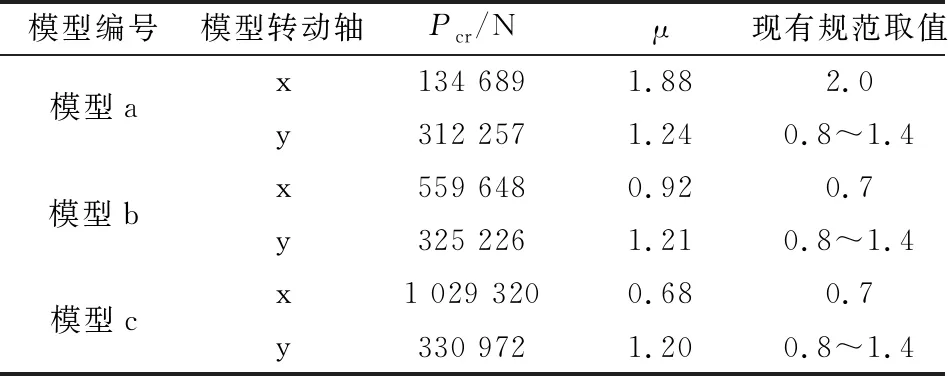
表2 三种模型中柱的计算长度系数

为验证计算结果的可靠性，将现有规范[4-5]中的取值与其进行对比。现有规范中指明构架柱设置端撑和未设置端撑时的计算长度为0.7、2.0；单跨、多跨构架柱的计算长度系数为1.4、0.8，所以但连续梁的高度不同时，构架柱的计算长度取值范围取为0.8～1.4。从表2中可以看出，沿x轴转动时，模型a和模型c的柱计算长度系数接近现有规范中相对应的取值；沿y轴转动时，3个模型构架柱计算长度系数均在现有规范的取值范围内，说明由分析结果结果较合理。在沿y轴转动作用下，当连续梁高度不同时，柱的计算长度系数宜取1.3；在沿x轴转动作用下，当柱中设置端撑时，柱的计算长度系数宜取1.0。以上柱计算长度系数的取值仅针对本文模型，对于其他类型的构架，应根据构架柱的具体情况进行相应的分析。

4 结 论

1)端撑杆件的存在有效抑制了构架柱的变形，构架模型中柱顶部的屈曲向量大小顺序为：模型a(未设置端撑)>模型b(柱中设置端撑)>模型c(设置端撑)。

2)连续构架梁的高度不同、柱中设置端撑会对构架柱的计算长度系数产生影响，其中，当连续构架梁高度不同时，柱的计算长度系数宜取1.3；当柱中设置端撑杆件时，柱的计算长度系数宜取1.0。

[ID:009842]