GeoGebra助力，创建乐学课堂——以“双曲线及其标准方程”为例

文∣王伯龙

双曲线是高中数学教学的难点，经过探索，教师可以借助GeoGebra软件，创设真实的数学情境，创建乐学课堂，提高学生数学学习的积极性。

一、技术支持，动态过程，探索发现

(一)创设问题情境，引发思考

【问题1】如图1，圆O的半径为定长r，A是圆O内一个定点，P是圆上任意一点。线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时，点Q的轨迹是什么？为什么？

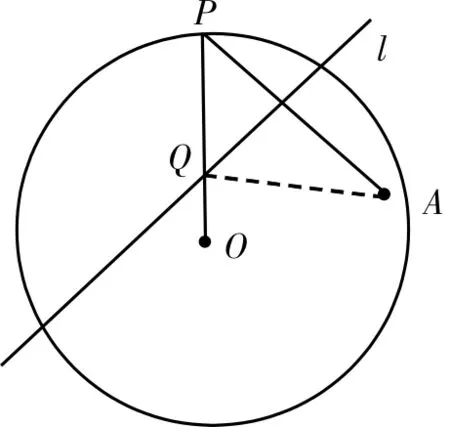
图1

学生观察图形，积极思考，发现O、A是两个定点，且|QO|+|QA|=r(r>|QA|)恰好满足椭圆定义的条件，得出点Q的轨迹是椭圆。从圆的层面感受到椭圆的形成。

教师通过问题驱动激发学生积极思考。问题的设置考虑学生的认知规律：先复习椭圆的定义；接着让学生在椭圆定义的引发下思考并解决问题1，加深对椭圆定义的理解；然后通过变式问题激发学生的求知欲。由此培养他们思考问题、发现问题、解决问题的能力。

【问题2】如果将问题1中的条件“A是圆O内一个定点”改为“A是圆O外一个定点”，其余条件不变(如图2所示)，那么，当点P在圆上运动时，动点Q所满足的几何条件是什么？你能画出轨迹图形吗？

图2

教师通过变式激发学生思考的积极性，学生观察图2，借助研究问题1的经验，很容易找出动点Q所满足的几何条件是|QA|-|QO|=r。

【追问】如果点Q在如图3所示的位置，又会得到怎样的几何条件呢？

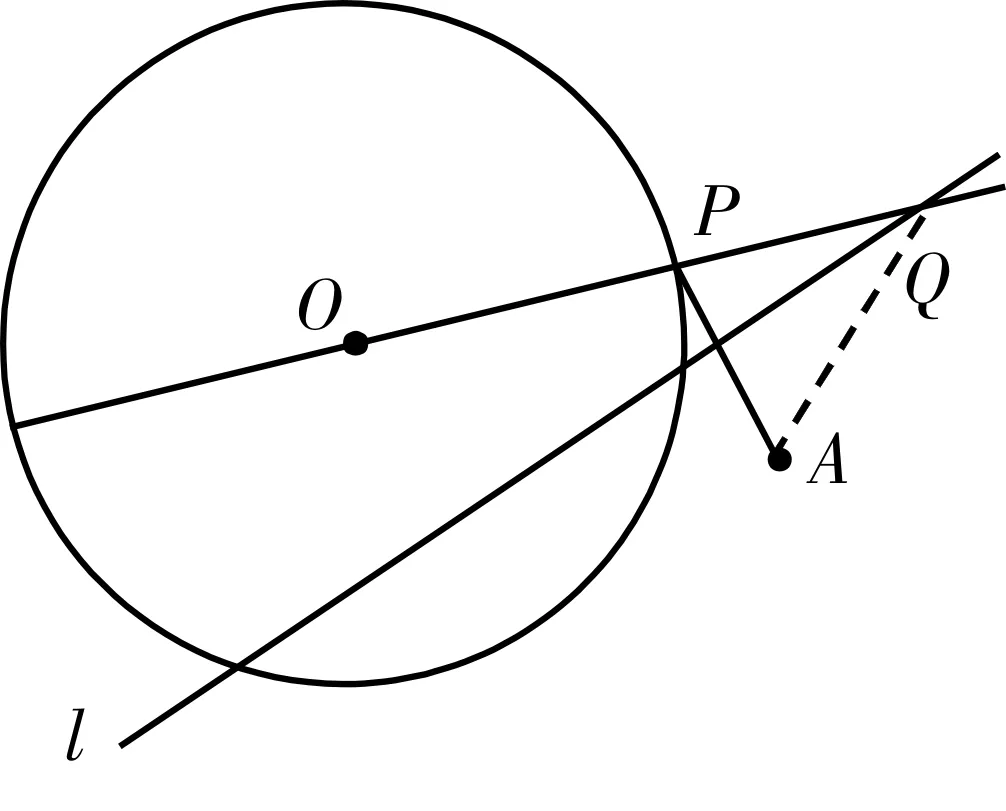
图3

学生通过思考，发现还有关系|QO|-|QA|=r,因而得出||QA|-|QO||=r。但点Q的轨迹是怎样的曲线，暂且不能解决。

(二)实验操作，提出猜想

教师让学生对问题2探讨分析，得出了动点Q所满足的几何条件是||QA|-|QO||=r，但点Q的轨迹是什么图形，学生依旧感到茫然。教师顺势带领学生完成以下实验来进一步探究。

【实验】让学生将图2画在作业纸上，然后按下列要求进行作图实验：

(1)保持点O、A的位置不动，在圆周上移动点P,再画出垂线l,找出点Q。

(2)重复(1)的步骤，每取一次点P,相应得到一个点Q。

(3)让学生不断地操作，尽量使得到的点Q足够密集。

(4)擦掉所有线段或直线，保留每个点Q(如图4所示)。

图4

【问题3】通过画图操作，说说：点Q的轨迹曲线你以前见过吗？你能猜想它是什么曲线吗？

教师提出问题，引导学生观察散点图思考、回顾，发现轨迹图形好像初中学习的反比例曲线、生活中热电厂冷凝通风塔的外轮廓线，猜想轨迹应该是双曲线。

动手操作是新课程倡导的学习方式之一，学生通过动手画图，亲身经历数学实验的活动过程。通过直观感知，激发他们的学习热情，培养他们发现问题、提出问题的能力，同时为下面的学习奠定了基础。

(三)GeoGebra助力，验证猜想

【问题4】根据作出的散点图，大家猜想点Q的轨迹是双曲线，那么它到底是不是双曲线呢？

教师引导学生分析，画图的过程中始终有||QA|-|QO||=r。只需验证满足条件||QA|-|QO||=r的点Q绘出的曲线是双曲线。然后，教师打开GeoGebra软件的绘图界面，在绘图区内画出图2，其中F1为圆心、F2为圆外一定点，将点Q设为追踪点，用鼠标拖动点P在圆周上慢慢运动，此时点Q的轨迹留在绘图上(如图5所示)。

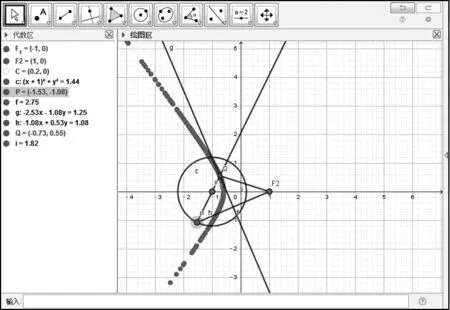
图5

【追问】为什么在图5中画出的是一支曲线？另一支如何去画？

学生思考讨论，发现在图5中始终有|QF2|-|QF1|=r成立。如果把满足条件|QF1|-|QF2|=r的图即图3中|QO|-|QA|=r画在绘图区内，就会有另一支曲线。

教师按学生讨论的结果进行绘图，得到另一支曲线(如图6所示)。

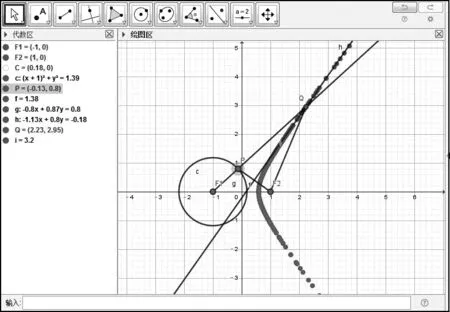
图6

通过学生动手画图得到点Q的散点图，提出猜想。再借助GeoGebra软件的动画演示，为学生学习创设了一个生动逼真的情境，使他们快乐地学习，积极地思考。同时，通过动画演示，验证了学生的猜想。

【问题5】图5、图6将双曲线的两支分开画在两个图中，不便于分析和研究问题。请大家思考，能不能将双曲线的两支绘在同一图上？

教师提出问题，学生思考讨论，教师引导学生寻找问题的本质。当点P沿着圆周运动时，中垂线l跟着运动，学生可以十分清楚地观察到双曲线是由一条条紧密的直线l包络而成的。教师在GeoGebra绘图软件中，将直线l设置成追踪线，然后拖动点P,绘出双曲线，如图7所示。

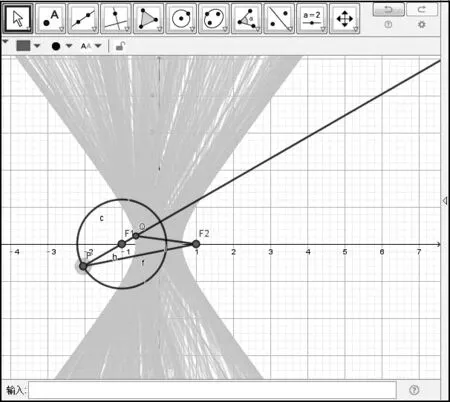
图7

从直线包络的角度分析动点轨迹的形成过程，利用GeoGebra软件更加逼真地演示了双曲线的形成，进一步验证了学生的猜想，体现了信息技术在数学教学中的应用。

(四)归纳总结，形成定义

【问题6】你能根据上面的活动，结合椭圆的定义，给双曲线下个定义吗？

教师提出定义：平面内与两个定点F1、F2的距离的差的绝对值等于常数(大于零，小于|F1F2|)的点的轨迹叫作双曲线。其中F1、F2叫作双曲线的焦点，两焦点间的距离叫作双曲线的焦距。

教师引导学生正确叙述双曲线的定义，对定义中的绝对值、常数的范围(大于零，小于|F1F2|)，让学生通过辨析加深理解。同时强调双曲线定义中要抓住关键点“两个定点，一个常数”。

通过思考、观察、动手实验、猜想、验证等一系列活动体验，类比椭圆定义中的定点、定长等的关系，归纳总结并表述双曲线的定义。培养学生数学语言表达能力和归纳能力，提升数学核心素养。

【问题7】根据上面的学习，我们已经知道双曲线的定义。请你拿出事先准备好的拉链，你能根据双曲线的定义，利用拉链画出一条双曲线吗？

学生按高中数学人教版选修2-1教材[1]中的叙述，拉开拉链的一部分，在拉开的两边上各选择一个点，分别固定在点F1、F2上，把笔尖放在拉链的合口上，随着拉链拉开或闭合，笔尖所经过的点就画出了双曲线的一支，调换位置，则可画出另一支曲线。

学生通过动手绘图，亲身体验双曲线定义的形成过程，从本质上加深对双曲线定义的理解，突出本节课的重点，渗透了数学文化。

(五)类比方法，建立方程

【问题8】椭圆与双曲线的定义中都有“两个定点，一个常数”这一关键点，回顾椭圆方程的建立方法和步骤，如何建系推导双曲线的方程？请大家尝试。

学生体会类比求椭圆方程的建系方法与方程的推导过程，取定点F1(-c,0)、F2(c,0)，定长为2a比较方便推导方程。

椭圆与双曲线的定义有相似之处，建立合适的坐标系、推导双曲线的方程完全由学生已有的认知经验，通过设点、建系、建立方程等活动来实施。一方面让学生充分感受数学知识之间的关联性，体会解析几何中的数学思想方法；另一方面通过化简、计算等培养学生“数学运算”的核心素养。

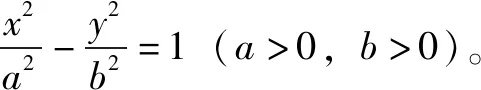
【思考】类比焦点在y轴上椭圆标准方程，如果双曲线的焦点分别是F1(0,-c)、F2(0,c),a、b的意义同上，这时双曲线的标准方程是什么？

教师提出问题后，有部分学生根据学习椭圆经验直接写出焦点在y轴上双曲线的方程；还有部分学生按照双曲线的定义进行计算化简得到双曲线的方程。对于这两种想法，教师都给予鼓励,并强调焦点在x轴和焦点在y轴上双曲线方程的特征，不要混淆。

(六)知识应用，深化理解

【例1】 已知双曲线两个焦点分别为F1(-5,0)、F2(5,0),双曲线上一点P到F1、F2距离之差的绝对值等于6，求双曲线的标准方程。

【例2】双曲线4x2-y2+64=0上一点P到它的一个焦点的距离等于1，那么点P到另一焦点的距离等于__________。

本节课的重点是双曲线定义的形成过程及标准方程的求法，学生通过练习，强化对定义的理解和对标准方程建立的步骤方法的掌握。让学生在学会基础知识的同时，学会研究问题的方法和技能；通过数学活动，积累解决问题的数学经验，提升数学核心素养。

最后教师进行课堂小结，提升学生能力。

二、技术助力，关注活动，以生为本

(一)GeoGebra助力，创建乐学课堂

《普通高中数学课程标准(2017年版)》强调，在数学教学中，信息技术是学生学习和教师教学的重要辅助手段，为师生交流、生生交流、人机交流搭建平台，为学习和教学提供了丰富的资源，教师应重视信息技术的运用，优化课堂教学，转变教学与学习方式。也应注重信息技术与数学课程的深度融合，实现传统教学手段难以达到的效果。[2]

本课设计中，通过GeoGebra软件的动态演示，为学生探究学习创设了一个乐学场景。在已有知识经验的基础上，通过创设动态变化的情境，让学生直观感受双曲线定义的形成和发展过程，更好地体会数形结合的思想，帮助学生发现数学规律，激发学生学习数学的热情。

(二)关注数学活动，展现逻辑思维

掌握“四基”、发展“四能”都离不开数学基本活动。数学教学的核心是发展学生的思维,优化思维，确保学生的思维到位，让全体学生参与知识发生、发展的全过程。在教学设计中要给学生多创造一些思考的机会，多留点思考的时间，多提供一些思维表达的平台。 本课设计中以问题串为引领，通过学生动手作图、用拉链画双曲线等一系列活动，经历数学探究、数学实验、数学猜想，归纳得出双曲线定义及推导双曲线标准方程等思维活动，使学生的思维深度得以加深和参与水平得以提高。

(三)树立生本观念，提升核心素养

《普通高中数学课程标准(实验)》强调指出：“要把数学的学术形态转化为学生易于接受和乐于接受的教育形态。”教科书上那些僵硬的、冰冷的、美丽的、形式化的数学知识，学生学起来比较枯燥乏味，理解起来比较困难，这就需要我们教师研读课标，钻研教材，分析学生，了解学情。在不违背课标要求，不破坏数学学科知识的科学性、系统性的前提下，努力理解和领会教材的设计理念和教学思路，把握教材的特点，根据教学内容和学生学情对教材进行选择、组织和排序等方式的 “二次开发”，对课程内容进行“校本化”“生本化”的处理，使课堂内容更加贴近学生的生活和经验,摆脱教材的束缚，做到“用教科书教”而不是“教教科书”。[3]

本课的设计考虑到学生的认知基础，从复习椭圆的定义开始，围绕着教材一道习题进行变式探讨，通过动手实验提出猜想，再到软件动态演示验证猜想，最后归纳出双曲线的定义，推导出双曲线的标准方程等，每一个环节都是在学生思维的最近发展区内进行设置。对于双曲线概念的生成过程，学生经历了动手实验、画图猜想、练习小结等活动，给予学生足够的参与机会。教学过程中始终关注学生思考、合作交流、动手操作、主动探索的学习方式，引导学生感受和领悟隐含在概念形成中的思想方法，在概念的运用和推广中渗透数学思想方法，促进学生的深度学习，实现育人的本位回归，将核心素养落到实处，使学生养成终身发展所需的必备品质和关键能力，真正实现素养教育。