探索动点的轨迹解动态几何问题

邹玉峰

(福建省华安县华丰中学 363800)

动态几何问题是历年各省市中考试卷中的常见题型.而探索动点的轨迹解动态几何问题是中考一种极其重要类型.探索动点的轨迹主要有两类：动点的轨迹是直线(射线、线段)或动点的轨迹是圆(圆弧).在求解此类动态几何问题时,因题制宜地把握运动规律，抓住特殊位置探索动点的轨迹，可使一些复杂的问题得到巧妙的解答.

一、动点的轨迹是直线(射线、线段)

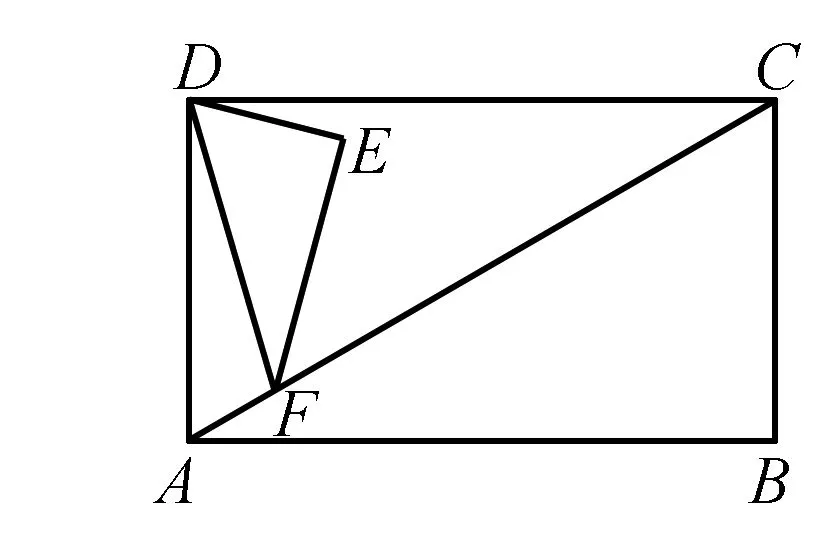
例1(2019贵阳中考)如图，在矩形ABCD中，AB=4，∠DCA=30°，点F是对角线AC上的一个动点，连接DF，以DF为斜边作∠DFE=30°的直角三角形DEF，使点E和点A位于DF两侧，点F从点A到点C的运动过程中，点E的运动路径长是____.

二、动点的轨迹是圆(圆弧)

例3如图，已知在△ABC中，∠ABC=90°，AC=4,BC=3,∠CPB=∠A,过点C作CP的垂线，与BP延长线交于点Q，则CQ的最大值为____．

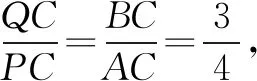
例4(2019桂林中考)如图，在矩形ABCD中，꾓点P是AD边上的一个动点,连接BP,作点A关于直线BP的对称点A1,连接A1C,设A1C的中点为Q,当点P从点A出发,沿边AD运动到点D时停止运动,点Q的运动路径长为____.

例5如图，等边△ABC中，AB=6，点D、E分别在BC和AC上，且BD=CE，连接AD、BE交于点F，则CF的最小值为____.

解决这类动态几何问题，关键是探索动点的轨迹，探求动点的轨迹是直线(射线、线段)或动点的轨迹是圆(圆弧)，使一些复杂的问题得到巧妙的解答.