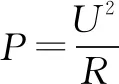巧用数理结合 轻松化解难题
程 颖
(江苏省睢宁县庆安中学 221200)
在初中物理中的光学、力学、电学等问题中经常出现一些抽象或解题过程过于繁复的难题,采用数理结合则有助于解决此类难题,在解题过程中也可以提升综合能力.数理结合是一种跨学科的融合,学生应注意培养这种思维方式.
一、数理结合,妙算距离
距离问题经常被考查,有时将这类问题转换为数学的长度计算则更便于求解.要求学生对此类物理问题理解透彻,将题干信息转换为数学信息,然后运用数学的思维方式进行求解.
例1 如图1所示,有一监测空气质量状况的气球静止的位于某一平静的湖面上空,距湖面20m高的仪器测得气球的仰角为30°.测得气球在水中虚像的俯角为60°,求气球矩湖面的高度.

图1

评注该类题目必须首先根据物理知识进行分析处理,对于求距离的问题在数学中的三角形中更容易解答,在解答过程中必须遵从物理规律,其次在运用数学知识时必须准确,不可以照搬硬套,“想当然”的思维方式必须摒弃.
二、数理结合,巧解极值
在初中物理中关于极值问题相对不多,但在一些竞赛题、压轴题中多会出现,极值问题多是物理中的难点,解决此类题可以结合数学的三角函数、比较法、假设法等方法.运用数学思想则可以将问题具体到数学的直接求解中,达到求极值的目的.
例2如图2所示,一杠杆长为L,它的一端A挂一重物G,为了使杠杆达到平衡,需用一定长的绳子将其拉住(S 图2 评注本题巧妙的将物理的杠杆原理与数学的三角函数方法相结合,将求物理极限的问题转换为数学的求极小值的问题.需要注意的是数学上有负值,但计算与生活实际相结合的物理问题时需要多加思考. 在解电路问题时由于公式的繁多导致求解困难,学生在学习过程中也可以尝试采用数理结合的思想,对未知量进行消除,采用换元法和因式分解技巧则可以轻松的对方程组进行化简,解这类题时需要学生明确未知量,等量代换正确消元. 例3 在电源电压不变的电路上连接一灯泡L1,灯泡的消耗功率为45W,在原电路上串联灯泡L1和L2,灯泡L2的实际功率因为10W,并且要比灯泡L1的功率要小,求两灯泡串联后灯泡L1的功率. 评注上述解法中运用了数学中的整体还原法和因式分解法,将繁复的方程进行了数学代换,减少了公式变换步骤,在保证解题准确的前提下提高了解题速度. 综上所述,数理结合的思想对于求解物理题有着重要的作用,合理的运用数学的方法和技巧可以简化解题过程,但在解题时首先应运用物理原理提取关键的信息,然后尝试采用数学方法求解.数理结合的基础是融会贯通的学好各学科内容,学生在平时应注意知识积累.
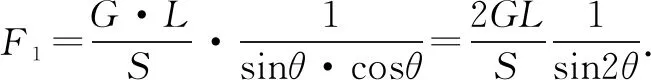
三、数理结合,简求电路