特殊值法在初中数学解题中的应用
陈素兰
(江苏省盐城市射阳外国语学校 224300)
一、特殊值法解选择题和填空题
在做选择题和填空题这两种题型时,往往这类题的解答不需要列出过程,用题目所给信息,整理综合并进行分析,根据题意确定特殊值,代入特征值,从而可得出结论.解题的正确性也大幅度地提了上来,从而也锻炼了学生敏锐的观察力和逻辑分析能力.
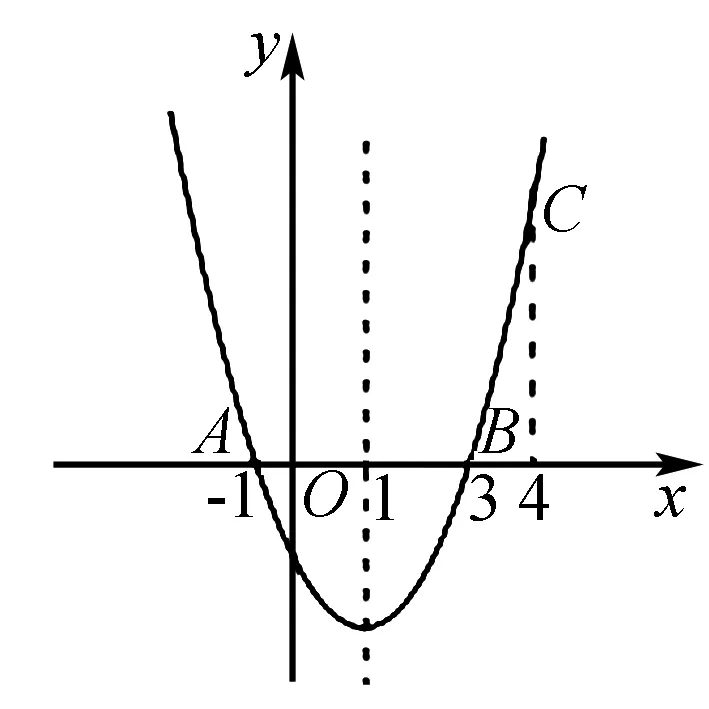

A.1个 B.2个 C.3个 D.4个

点拨本题主要考查二次函数的性质,利用对称性和单调增减性,求解出此抛物线的对称轴、最值及取值范围等.此类题解答时要有耐心,逐一探究分析并验证,解答不出时看是否能赋特殊值进行接下来计算,往往用特殊值法,能巧妙地进行解答.
二、特殊值法解运动型题型
初中数学中常见一种给出变量的范围但结果有待讨论的运动型题型,对于这一类型的题型,关键点在于选择一个参考点即取一个特殊值,再由特殊值展开分析讨论,逐步破解没有解题思路或思路不清晰的现象.

例2如右图,在直角三角形ABC中,∠ACB为直角,过C点作CD垂直于AB,垂足为D点,E为AC边上任意一点,连接BE且交CD于G点,作EF垂直BE,与AB交于F点,如果AC=aBC,CE=bEA(a、b均为实数),问EF与EG有怎样的数量关系.

点拨本题所涉及的知识点主要为全等三角形和相似三角形的判定与性质.当拿到这题时不知从哪里下手去解决,此时可以分析一下,若探究两者的数量关系,且没有其他限制条件,必存在特殊值情况,因此可选1为特殊值,再逐层往下探索,思路便越来越清晰,即可轻松解答此题.
三、特殊值法解化简题和规律题
数学这门学科具有应用性、灵活性、抽象性及准确性四个特点,这里的准确性就需要在数学题中做到检验.检验能力是做题中更高能力的要求,不仅要看之前做的步骤是否正确,而且在检验时还需要学生具有很强的抗干扰能力,从而减少出错率,提高解题效率.特殊值法在检验化简题和规律题中更能显著体现.
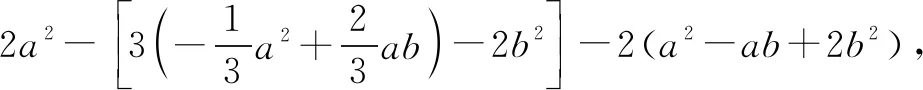

点拨本题所涉及的是整式的加减这部分知识点,解答本题的关键为合并同类项,即整式加减的实质.对于这种题型学生在解答时经常会出错,给的这么长的题目终于化简出了结果,一开心就直接把值代入得出最终结果,却不知是否化简正确,特殊值检验是减少做题失误的最有效的方法,不仅做题速度要快,准确率也要高.
总之,数学的解题可以有效地提高学生的逻辑分析能力,在日常教学及学生做题中要重视解题的方法多思考、多总结.特殊值法是解决数学问题的一个转折点,复杂问题特殊化,对题目的认知水平难度降低,由浅入深,解题思路清晰,快捷高效解题,同时有利于学生观察能力的提高,逻辑推理能力的发展.

