基于滚动时域优化策略的多载AGV充电调度

丁 一， 陈 婷

(上海海事大学 物流科学与工程研究院， 上海 201306)

近年来，随着全球贸易量不断增长，集装箱运输的市场需求逐渐增多。港口运营商不仅要面对集装箱吞吐量不断增长的压力，而且要面对降低集装箱港口运营成本的压力。目前，各大自动化集装箱码头均已使用以电能为动力源的自动导引运输车(Automated Guided Vehicle, AGV)。SCHMIDT等[1]结合集装箱码头的大型电力项目数据，分析在集装箱码头运营中采用以电池为动力源的AGV的商业可行性，实例验证结果表明：该方式可使码头运营商节省10%以上的总支出。

越来越多的学者对多载AGV进行研究，这反映了多载AGV在码头应用的广泛性和多载AGV相比单载AGV的优越性。电力驱动的AGV本质上是无人驾驶的电动汽车，由计算机控制系统控制，与港口岸桥和场桥等其他设备协同调度。集装箱港口的控制系统复杂多变，有许多不可控的因素，如设备故障和设备延迟等。总体来说，在港口对多载AGV进行调度是一个非确定性多项式难题(Non-Deterministic Polynomial Hard, NP-Hard)，对在确定环境下建立的模型进行优化计算所得结果可能无法适应港口真实复杂的环境。

多载AGV存在运输任务难以确定、交付地点难以选择、装载调度复杂和负载选择多变等困难，其调度比单载AGV更复杂。HO等[2-3]在不同的情境下对9种装载规则进行对比分析，结合卸载规则，通过数值分析求解出最优规则组合。霍凯歌等[4-5]从作业费用、完成时间和空载率等方面对多载AGV和单载AGV进行对比分析，采用遗传算法验证多载AGV不仅能提升自动化集装箱码头的作业效率，还能减轻交通拥堵的情况。CHAWLA等[6]使用模因-粒子群组合算法缩短多载AGV的最短完成时间和最短等待时间，在不同规模的试验中有效地解决多载AGV的调度问题。

GRUNOW等[7-8]考虑到多载AGV在自动化集装箱港口的工作环境和自身调度的动态性，利用车辆的有效性提出一种基于优先权的调度算法，将多载AGV装载状态分为AGV完全可用、AGV部分可用和AGV不可用等3种状态，通过建立混合整数规划(Mixed Integer Linear Programming,MILP)模型验证基于滚动时域的优先权调度算法的有效性。KLERIDES等[9]提出对多载AGV执行滚动时域，既可使用于调度的信息在一定的时间间隔内更新，又能执行新的调度方案，对该方法在不同规模的港口中进行实例分析，验证滚动时域的方法能使多载AGV快速适应复杂且动态的工作环境。刘国宝等[10]采用改进的滚动时域优化策略验证动态调度方法的有效性。宋李俊等[11]基于滚动时域优化框架，设计出适于在故障情况下应用的周期与事件混合驱动的动态调度策略，采用遗传算法对动态调度模型进行求解，通过仿真试验验证该策略的可行性和有效性。BIAN等[12]提出一种考虑电池容量约束的事件驱动分配模型，当事件发生时，AGV执行新的调度方案，通过与现有的算法相比较，证明这种动态调度算法适用于AGV的动态调度。

上述研究主要集中在多载AGV运输任务的确定、交付调度、装载调度和负载选择等方面，而对多载AGV运输动态调度开展的研究较少，同时未考虑电量、负载等约束条件。本文研究电量约束和负载约束条件下的电力驱动多载AGV，采用先到先服务(First Come First Service,FCFS)的调度策略建立MILP模型，在滚动时域框架下，采用周期与事件相结合的混合驱动调度方法，对电力驱动的多载AGV进行动态调度分析。

1 问题描述

自动化集装箱港口的AGV主要分为装载20英尺(1英尺≈0.304 8 m)箱的小型AGV和装载40英尺箱的大型AGV。在传统单载模式下，任何时刻AGV只需处理1个集装箱，其尺寸对AGV的作业效率没有影响。在多载模式下，AGV必须考虑多个负载和AGV电量、容量的限制，考虑集装箱尺寸，从而进行有效的调度已成为必不可少的条件。本文根据不同尺寸大箱的占比，分析在不同滚动周期下多载AGV的作业效率，充分发挥多载AGV的优越性。从AGV的角度看，每个任务只需考虑起点和终点，集装箱卸船作业和装船作业对AGV并没有本质上的区别,因此只需研究装船作业下的AGV调度。

为便于调度，本文假设所有AGV最多同时装载2个20英尺箱。自动化集装箱码头俯瞰图见图1。 AGV一旦收到运输请求，即从充电站出发开始执行运输任务。有两个运输任务的多载AGV工艺流程见图2。AGV收到运输请求后立即从充电站出发，根据FCFS的装载调度规则确定集装箱的装载顺序，根据最短距离的交付规则确定集装箱卸载顺序。AGV在确定集装箱的装载顺序之后，会检查是否有足够的箱位和电量来完成任务,在箱位和电量充足的情况下完成接下来的运输任务，若箱位和电量不能同时满足运输要求则仅完成当前的任务。

注：①为岸桥；②为码头前沿中转平台；③为AGV运行轨迹；④为AGV小车；⑤进场中转平台；⑥为场桥

图2 AGV工艺流程图

2 混合驱动的滚动时域优化策略

2.1 AGV的可用性

每次发出调度请求时，都应对等待运输的任务和可用的AGV进行重新分配。目前，许多学者都认同GRUNOW等[7]提出的AGV可用性划分，结合AGV的容量和电量约束条件，针对即将执行的任务分情况分配调度:若AGV电量满足且空车，则AGV完全可用；若AGV电量满足且AGV有剩余箱位，则AGV部分可用。对于AGV不可用的情况，主要有4种情形，即：AGV电量不足且空车；AGV的电量不足但有剩余箱位；AGV的电量不足且AGV没有剩余箱位；AGV的电量充足但没有剩余箱位。例如：多载AGV已装载第1个20英尺的集装箱，并已通过FCFS的装载调度规则确定第2个20英尺集装箱的信息，若经检验满足AGV电量充足且有剩余箱位的条件，则对于第2个20英尺集装箱而言，AGV部分可用。

从调度的角度看，对于即将到达的集装箱，AGV不可用，但对于下一个即将到达的集装箱，AGV可能可用。为更好地完成AGV的装载运输任务，本文提出基于混合驱动的滚动时域优化的动态研究方法，该方法将周期与事件的动态调度优点相结合，对多载AGV进行更加有利的分配。

2.2 基于混合驱动的滚动时域优化策略

针对自动化集装箱码头多载AGV的动态调度问题，主要有周期型调度策略、事件驱动型策略和周期与事件相结合的混合驱动的滚动时域优化策略等3种动态调度策略,其中:周期型调度策略是指系统每隔固定周期进行重新调度，要求周期的长短与实际相符合;事件驱动型调度策略是指通过定义突发事件来进行重新调度。本文采用基于周期与事件相结合的混合驱动的滚动时域优化策略。当发生定义的突发事件时，采用事件驱动调度，对突发事件作出快速反应，否则采用周期调度。该调度策略既削弱对定义事件的依赖性，又增强滚动优化的稳定性，以时间作为滚动窗口推动系统不断更迭。在t时刻按局部调整并执行运输任务,经过滚动周期时间后将已完成的任务移入完工窗口,再从等待运输的任务中选取时间Δh内的任务进入预测窗口,在t+ΔT时刻开始进行周期调度决策。基于时间的窗口滚动示意见图3,其中:F(i)为第i个完工窗口;P(i)为预测窗口;W(i)为等待窗口。在预测窗口P(i)中,结合事件驱动的调度进行再调度。Δh为AGV无法完成本预测窗内的订单时所能接触到的下一个预测窗内任务所在的时间段。

图3 基于时间的窗口滚动示意

根据完全可用条件规则，当事件发生时，只有AGV的电量和箱位都充足才分配任务给AGV。根据AGV的状态定义3种触发事件，即：

1) 在给定的时间窗口出现新的订单。

2) AGV完成最后的订单。

3) AGV无法完成本预测窗内的订单，但能完成下一个预测窗内的订单。

当窗口中出现新任务时，需及时调整AGV的分配，如事件1；当系统中没有需要运输的集任务时，AGV不再进行分配，如事件2；事件3可确保AGV能及时更新调度信息，充分利用AGV的装载能力。

3 模型建立

3.1 符号说明

无论是装船还是卸船，都需在时间窗内完成。t为预测窗口开始的时间节点，ΔT为滚动周期。在时间(t,t+ΔT)内有m(m∈M)台AGV完成I个集装箱的装卸运输任务。(i+，i-)为同一集装箱的装载与卸载操作。在装载操作过程中，1个20英尺的集装箱要占1台AGV的1个箱位，1个40英尺的集装箱要占2个箱位；在卸箱操作过程中，卸载1个20英尺的集装箱，AGV的容量减少1个箱位，卸载1个40英尺的集装箱，AGV的容量减少2个箱位。具体符号定义见表1。

3.2 调度模型

以最小化最末任务完成时间为目标，建立自动化集装箱码头多载AGV调度模型，该模型的目标函数与约束条件如下:

目标函数 minf

(1)

s.t.f≥zimt, ∀i∈I

(2)

xi1i2m(Ei1m+Ei2m)≥max{Ei1m,Ei2m},

∀i∈I;m∈M

(3)

(4)

max{zi1mt,zi2mt}≤xi1i2m(zi1mt+zi2mt),

∀i∈I;m∈M

(5)

xiim=0, ∀i∈I

(6)

xi+i-m=1, ∀i+∈I+;i-∈I-

(7)

表1 符号定义

qi2m=di1+di2+N(1-xi1i2m), ∀i+∈I+;m∈M

(8)

di≤qim≤Qm, ∀i+∈I+

(9)

0≤qim≤Qm+di, ∀i+∈I-

(10)

yi1i2mt(Rmt-max{Ei1m,Ei2m}))>R,

∀i∈I,m∈M

(11)

yimt=

(12)

xi1i2m∈{0, 1}, ∀i∈I

(13)

zimt>0,t>0,f>0, ∀i∈I;m∈M

(14)

式(1)为目标函数，旨在使最末任务完成时总作业时间最短；式(2)为保证任务顺利完成，最末任务的完成时间大于等于任意任务的完成时间；式(3)中，若AGVm执行多载操作，且i1的优先级高于i2，则总耗费的电量小于等于分别装载i1和i2耗费的电量；式(4)考虑两个相继任务，只能一个任务比另一个任务先执行；式(5)为若AGVm执行任务i1后立即执行任务i2，则到达任务i2卸载的时间小于等于单载运输的时间和；式(6)为任务本身不能成为自身的上一任务；式(7)为对于同一个任务，必须先执行装载操作，再执行卸载操作。式(8)～式(10)为AGVm的容量约束，其中:式(9)反映装载操作的AGVm容量不能超过AGVm的同时所负载的最大容量:式(10)为在卸载操作的AGVm上没有负载的集装箱后，也不能继续执行卸载操作；式(11)为AGVm只有在剩余功率足够用于完成任务的情况下才能被分配给任务i1和i2；式(12)为决策变量yimt的定义，只有当AGVm的容量和电量同时满足时才参与分配。式(13)和式(14)为变量的约束条件。

4 案例分析

AGV的相关参数设置见表2。在上海港洋山4期自动化集装箱码头停靠的某集装箱船的装卸作业数据见表3，由于数据量过大，仅列出部分数据。表3中：根据最早时刻的大小，按升序进行任务编号；作业的4个堆场分别用数字1、2、3、4表示；2台桥吊在海侧为该船服务，数字5、6分别表示2台桥吊。有10台AGV进行水平运输，假设 AGV的安全电量为总电量的10%，可保证AGV从码头任意位置返回充电站。

表2 AGV参数设定

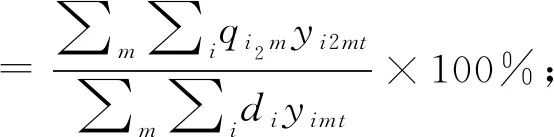
1) 分别以30个任务、60个任务和90个任务为研究对象，对多载运输进行实例分析，并根据40英尺箱占比的变化对完成时间、容量利用率和电池利用率进行对比分析。有4辆AGV进行服务，涉及4个堆场和2台桥吊，ΔT=1 000。运行结果见表4。由表4可知：当大箱占比30%时，任务量的变化对容量利用率和电池利用率的影响较小。在任务量相同的情况下，大箱占比越少，小箱占比越多，AGV能在越短的时间内同时运输更多的集装箱，缩短完成时间，AGV的空载时间越短，电池利用率越高。然而，考虑到AGV在不同运输状态下的耗电量和运输速度存在差异，过多的小箱反而会增加AGV的负荷，达不到降低完成时间、提高电池利用率的效果。结合实际情况可知：40英尺箱占比约30%是最理想的状态。

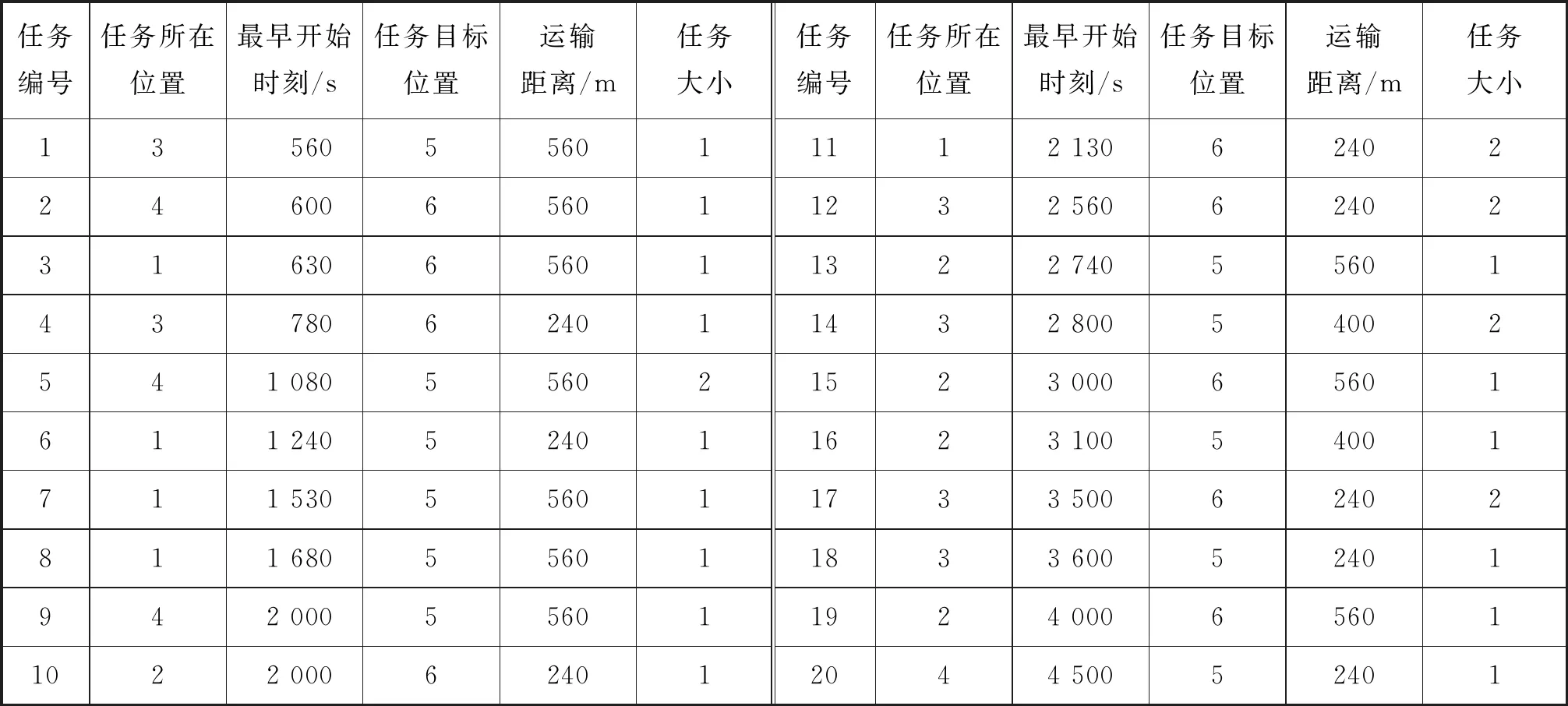
表3 任务属性表

表4 运行结果对比

2) 根据动态调度策略，突发事件发生时采用事件驱动型策略，其余时间采用周期性滚动机制。在周期性滚动机制下，滚动调度的次数和系统对动态因素的适应能力由ΔT决定，故设置不同的滚动周期值分别进行试验，以验证ΔT与评价指标的相关性。不同滚动周期调度结果对比见表5。为使试验结果更具有说服力，试验保持在同一情景下进行，取I=10。由表5可知：当周期ΔT=800～1 300 s、滚动次数为2～4次时，AGV动态调度作业效率最好，目标函数值达到最优，电池利用率较高。对试验结果进行分析可知：在滚动时域优化调度策略中，滚动周期的取值影响整体的调度效率，周期过长时无法对系统中产生的干扰进行快速反应，周期过短则会使重新调度过于频繁，导致整体任务完成时间延长，AGV电池利用率也不理想。

表5 不同滚动周期调度结果对比

3) 为更好地验证多载AGV的优越性，将多载AGV与单载AGV完成相同任务量所需的时间相对比,结果见图4。当任务量为10个时，多载AGV的完成时间与单载AGV相差不大;当任务量增加至300个时，多载AGV的完成时间相比单载AGV明显减少。这表明，在大多数情况下，多载AGV能在更短的时间内完成任务，从而满足自动化集装箱码头对提高码头水平运输效率的要求,同时随着任务量的增加，多载AGV的优势更明显。

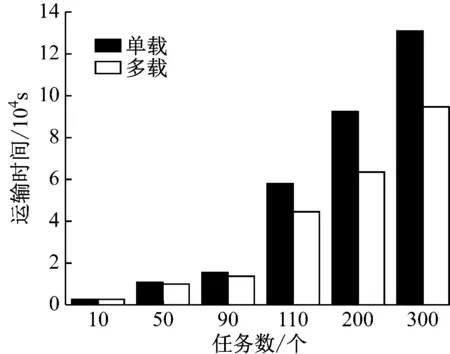
图4 单载 AGV 与多载 AGV对比

5 结束语

本文对多载AGV的作业调度进行研究，基于滚动时域的优化策略建立相应的MILP模型。试验结果表明：当40英尺箱占比约30%时，能最大化多载AGV的运输能力；ΔT的取值会影响作业效率，需根据实际情况对ΔT进行合理取值，在40英尺箱占比相同的情况下，任务量越多，多载AGV的效率越高。目前，多载AGV在港口水平运输中的占比越来越大，对多载AGV进行充电调度研究有利于提高其工作效率。本文的研究结果可供码头多载AGV充电调度参考，以便码头对多载AGV进行调度管理，提高港口水平运输设备的整体作业效率。但是，该研究并未考虑AGV在充电站的等待时间和AGV的数量差异等因素，这些将在未来做进一步的研究。