超大型油船冰区靠泊关键技术——以大连长兴岛恒力石化码头为例

李 林

(大连港引航站， 辽宁 大连 116001)

1 大连长兴岛恒力石化码头冬季冰情对船舶靠泊的影响

1.1 冬季冰情概况

恒力石化30万t码头位于大连长兴岛北部高脑子海域已建好的北港区(恒力石化港区)西防波堤西侧水域，轴线为62°～242°。该区域冬季常风向为NW，次常风向为NNW，区域内受季风的影响较大。因此，冬季NW风极易将浮冰吹向码头，其分布态势大致与长兴岛北港区东西防波堤平行，平整冰厚度一般为30.0～47.6 cm，并伴有碎冰。此种冰情受风向和风力影响甚烈：风向越接近W，风力越大，因碎冰向岸拢去形成的岸侧冰情越严重。风对冰量的影响分布见图1。渤海冰情等级随时间的变化见图2。

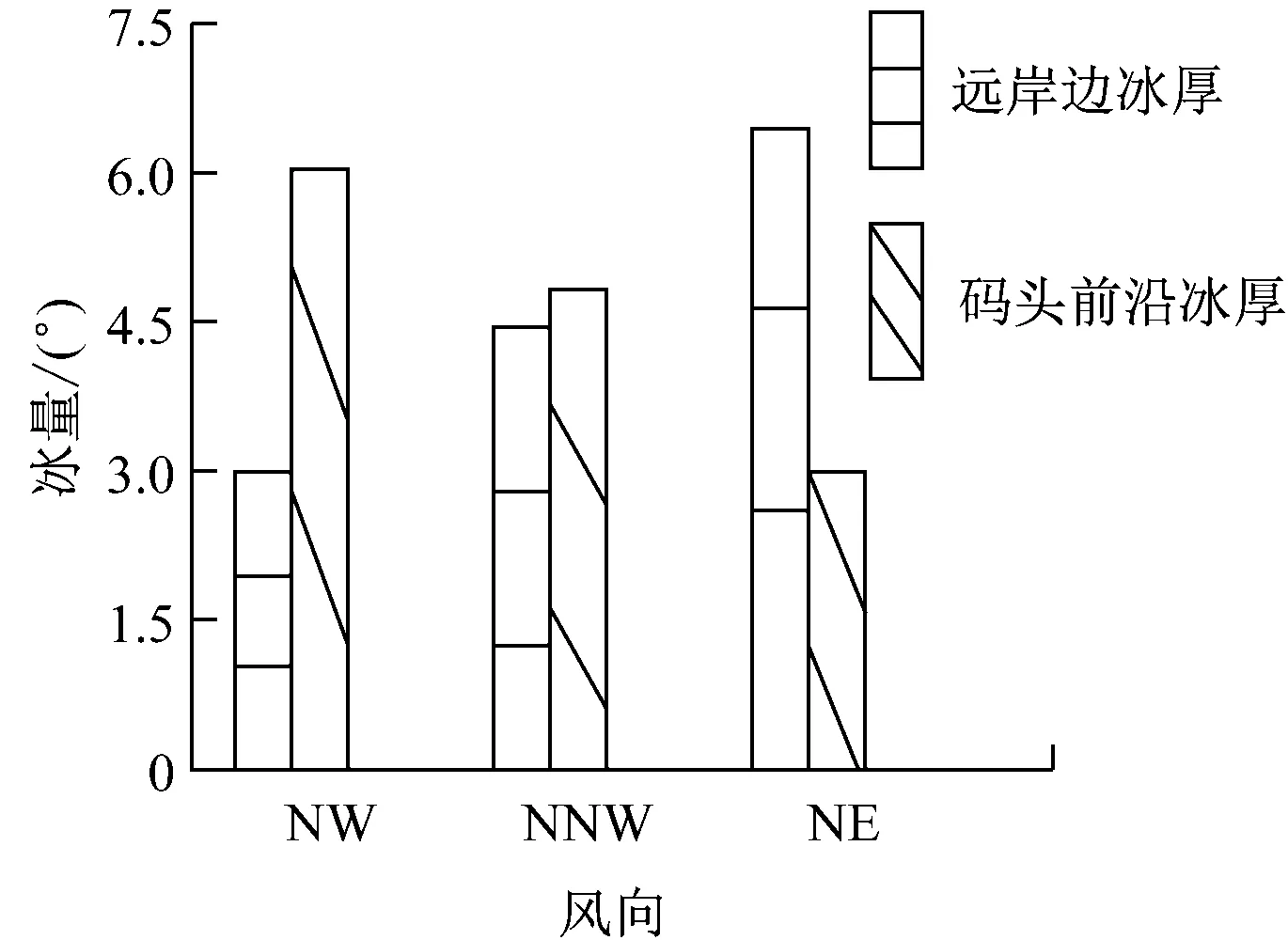
图1 风对冰量的影响分布

图2 渤海冰情等级随时间的变化

1.2 冬季冰情对船舶靠离泊影响

由图2可知:恒力石化码头每年12月到翌年3月会有大量平整冰和碎冰浮动，且近岸冰情受W风的影响更大。上述冰情态势对超大型油船(Very Large Crude Carrier,VLCC)靠泊时各种与安全相关的内外因素的影响如下。

1.2.1影响人为因素

冰情严重会对引航员和船长的心理形成巨大的震慑，易于造成船舶驾驶人员心理扭曲，在焦躁中蛮干，致操船方法失宜。

1.2.2影响外部环境

(1) 当浮冰严重时，可在距岸1 km范围内形成浮冰集聚区。当船舶因特殊原因不得不在长兴岛恒力石化港区防波堤外抛锚时，有可能在重新起锚过程中因浮冰堆积而导致绞锚困难，严重时甚至丢锚或使锚链受损。

(2) 恒力石化防波堤走向为62°～242°，防波堤口朝西侧。因此，受偏西风影响(冬季多为NW向)，每年12月至翌年3月，碎冰和平整冰往往随着洋流位移。大量浮冰会顺风涌向防波堤(甚至码头边缘)，阻塞航道和码头。同时，当平整冰厚度达到20～30 cm时，船舶基本上不能自力破冰航行，甚至会被冰夹住，产生随冰漂流的险情。VLCC的满载吃水通常在20 m以上，即便半载,通常也有约18 m的吃水，如果随冰漂移至浅水区域，极易引发搁浅事故。

(3) 当冰情严重时，码头与船舶间始终存有大量浮冰，阻滞船舶如期贴靠码头。

(4) 当冰情严重时，拖船极易出现主机因海底阀被冰堵而停转和锚链损丢的情况，导致拖船(甚至是破冰拖船)“骑”上碎冰而无法移动等危险。此时，拖船自身安全难以保证，对于靠离泊需要拖船辅助的30万吨级油船而言，极易诱发失控的隐患。

1.2.3影响VLCC的结构与设备

(1) 当浮冰存在时，如果船舶的海底阀使用不当或没有转入内循环冷却水系统，浮冰有可能进入海底阀堵塞循环冷却水系统，造成船舶主机出现故障。

(2) 在螺旋桨沉深不足的情景下，停车易被冰困，而盲目倒车易导致螺旋桨碰冰受损，陷于进退维谷的境地。

(3) 当冰情严重时，船舶一般采用慢速快车的方法破冰，即缓慢触碰浮冰，逐渐加大主机转速，加大船舶推力破冰。但是,长时间地采用此法易致船舶主机负荷过载，产生安全隐患。

2 冰区靠离泊的关键点分析及超角度靠泊方案

综上可知，解决VLCC冰区安全靠泊的关键是减小冰对船舶靠岸的影响。

VLCC靠泊,特别是满载靠泊时，为克服船体的巨大惯性，船长会选择拢流靠泊法，即利用拢流顶推大船和拖船顶推大船的合力来缓慢平推大船进入泊位。然而,为避免大船因合力而过快地拢向码头，通常采用增加横距的方法。一般情况下，船与码头的横距以0.1～0.2 n mile为宜，流急时会达到0.3 n mile以上。但在冰区靠泊过程中，当冰区由冰泥固结的软冰层组成时，冰阻力远大于水阻力。因此，流对大船的顶推影响可忽略不计。此时，大船受到的冰阻力过大，拢流压力过小，如果采用常规的单独依靠拖船顶推大船靠泊码头的办法，往往因冰阻力大于拖船推力而使大船不能入泊。因此，VLCC在冰区靠泊过程中需解决两项技术难题,即：

1) 船舶在靠泊码头过程中的转向角度要能减少船岸间冰量，使得冰阻力等于或小于船舶平行码头后的拖船阻力；

2) 按照上述角度实施转向的最晚施舵点。

为解决这两个难点，本文提出VLCC冰区靠泊的超角度靠泊法。

2.1 VLCC冰区靠泊的超角度靠泊法

超角度靠泊法是指在靠泊过程中扬弃传统的平行抵泊法，改用增大入泊角度、减小入泊横距，以减小大船与泊位之间的冰量，从而减小冰阻力的方法。见图3。

图3 VLCC常规靠泊与超角度靠泊示意

2.2 超角度靠泊法特点

较之传统平行抵泊法，超角度靠泊法有以下特点：

1) 船舶用于接近泊位的“旋回”范围增大。

2) 船舶接近泊位的角度较大。

3) 船舶和泊位间的冰量减少,冰阻力减小。

超角度靠泊法旨在减少船舶与泊位间的冰量，从而减小冰阻力对靠泊的影响。船舶在碎冰区域航行时与冰相互作用的阻力远大于与水相互作用的阻力(见图4)。

图4 船舶速度与阻力的关系

显而易见，超角度靠泊法的最大优点在于船舶航向与码头走向的入泊角度较大，横距较小，有利于减少冰量和减小冰阻力，从而易于大船靠泊。但是,其不足之处在于因船舶与码头入泊角度较大，易给驾驶人员造成视觉上的冲击，心理上造成负担，以为大船始终与码头有交角，难以平行入泊，担心发生船舶与码头碰撞的事故。因此，超角度靠泊法的实施关键是寻求大船入泊角度，寻求与码头走向平行的最晚施舵点。

2.3 最晚施舵点与入泊角度的数学模型分析

2.3.1最晚施舵点数学模型

船舶在采用最晚施舵点后平行于码头时，需靠拖船顶推入泊。此推力应大于等于冰阻力，且在顶推入泊过程中，船舶的变形应为可逆变形，即因冰与拖船的作用力而产生的船体变形应在许可的弹性模量的物理范围内。鉴于此，引入冰的弹性模量与冰的体积之间的换算关系，通过计算船舶新航向距离和拖船顶推力，建立关于最晚施舵点的换算关系的数学模型。

最晚施舵点至码头的距离为L(见图5)，最小转向施舵距离L的计算式为

L=Dnc+b

(1)

式(1)中：Dnc为转向过程中的新航向距离，m;b为大船与码头中间冰的宽度，m。

由式(1)可知:在计算最晚施舵点到码头的垂

图5 最晚施舵点到码头垂直距离L示意

直距离时,需先计算出新航向距离Dnc与大船与码头中间冰的宽度b。以下为Dnc与b的数学模型推导。

Dnc的计算式为

(2)

式(2)中:vs为旋回初速度，m/s;K和T为船舶操纵指数;t1为操舵时间，s;δ为操舵角，(°);φ为转向角，(°)。

新航向距离计算示意见图6。

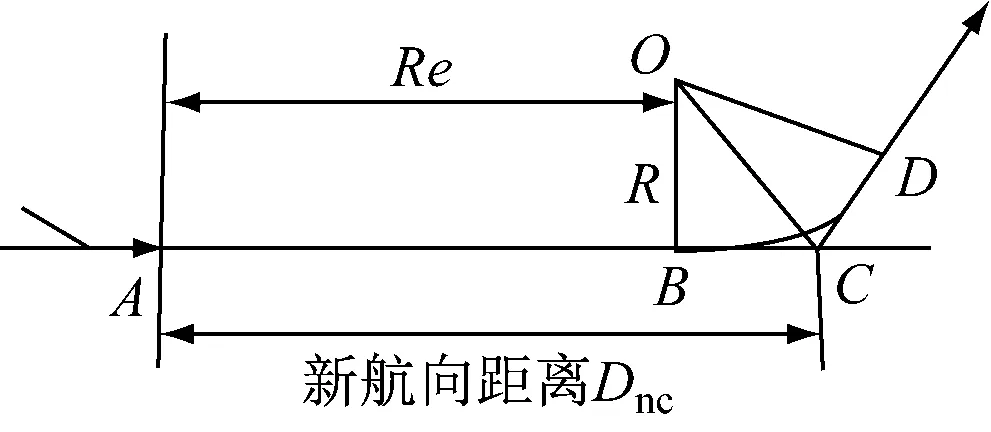
图6 新航向距离计算示意

b的计算式为

(3)

式(3)中：h为冰的厚度，m；Vb为船舶与码头间冰的体积，m3；l为船舶长度，m。

在已知船舶l和h(可根据当地气象预报得出)的前提下，通过下列数学推导可得船岸间冰的Vb。

船岸间冰对船舶的阻力(Fb)应小于等于协助大船靠泊的拖船的总推力F，即

Fb≤F

(4)

F的计算方程式如下:

先计算出VLCC满载所需拖船总功率P，即

P=TDW×5.15%

(5)

式(5)中:TDW为船舶总载重量,t。

根据总功率可计算出拖船总推力为

(6)

因式(4)中Fb≤F，可计算出冰阻力Fb的极限值，即Fb=F。

通过Fb的极限值与海水密度、海冰与船舶接触面的投影宽度之间的数学关系，可计算出海冰的特征长度。计算式为

(7)

式(7)中:ks为海水密度,kg/m3;D为海冰与船舶接触面的投影宽度，m;li为海冰的特征长度。

根据li与冰的弹性模量的关系可得冰的弹性模量E为

li={Eh3/[12(1-n2)ks}0.25

(8)

式(8)中:h为海冰厚度，m;n为泊松比，船舶在冰区中的泊松比经验值为0.25～0.36，推荐值为0.30。

根据E与冰体积之间的关系，可得

(9)

在计算出Vb后，根据式(3)可算出b值，根据式(1)可算出转向施舵的最晚施舵距离L。

2.3.2入泊角度的数学模型

在计算冰中最晚施舵距离L、选择转向时机时，亦需参考船舶的入泊角度。为减小Vb，船舶在冰中的入泊角度要大于在静水中的入泊角度(见图7)。

图7 静水入泊角度与冰区入泊角度对比

根据文献[13]可得船舶在冰中旋回运动时漂角与冰对舵阻力的关系。因此，在计算出冰对舵阻力的前提下，根据漂角与冰阻力的关系可得漂角的平均值。根据漂角与角速度的关系式可计算出船舶在冰中的旋回角速度，再根据角速度与时间的乘积等于入泊角的关系式，便可得到入泊角度。

具体计算式为

θ=ω·TC

(10)

式(10)中:θ为船舶冰中靠泊入泊角，(°);ω为旋回角速度，(°)/min;TC为旋回运动时间，min。式(10)中ω的计算式为

(11)

式(11)中:v为航速，m/min;R为船舶回转半径，m;β为漂角，(°);t2为旋回时间，min。

由此可得知船舶冰中旋回的漂角，进而可通过式(11)计算出船舶的ω。

另外,由文献[13]可知:通过漂角β和冰阻力的试验数据可列表查出在不同冰阻力的作用下漂角β的数值(见表1)。

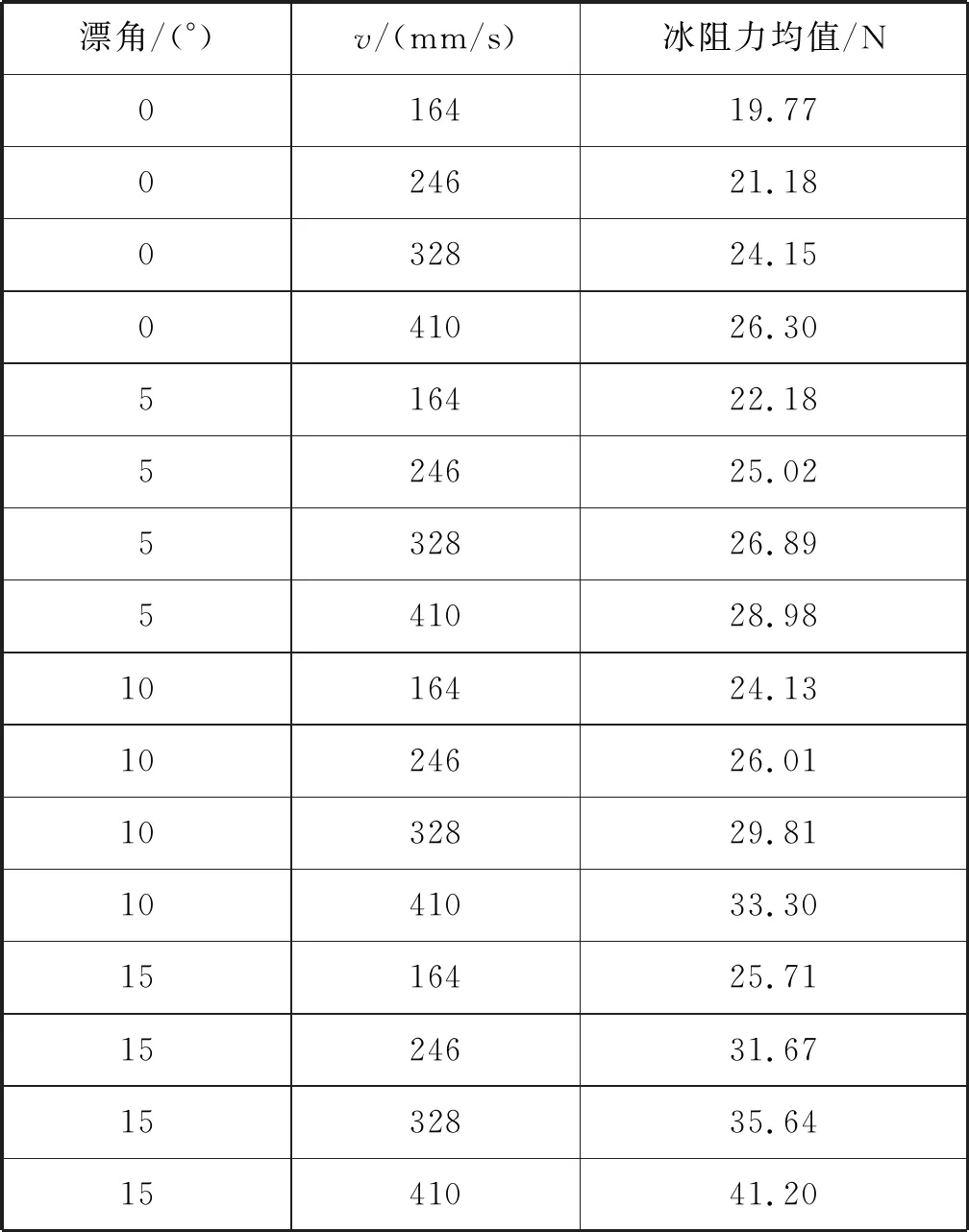
表1 冰船相互作用模型试验阻力均值与漂角关系

由表1可知:在不同冰阻力前提下，通过冰阻力计算可得到对应的漂角。

由文献[14]可知冰阻力计算式为

(12)

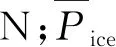
由式(12)可得Pice，据表1可查得漂角β，再据式(11)可算出旋回角速度ω，最后据式(10)取得入泊角θ。

3 结束语

目前,国内外针对船舶冰区靠泊的研究尚处于起步阶段，本文论证VLCC冰区靠泊的关键技术，从理论上提供了解决这一难题的一种实践方案——超角度靠泊法，这对于确保冰区靠泊作业安全具有一定的理论指导价值和实践借鉴意义。但考虑到冰区靠泊过程中冰情、洋流和海浪等因子对船舶的干扰度难以量化，故在具体的操作实践中尚需援以相关的技术协调，如VLCC冰区航前准备、应急预案的准

备和码头方面的配合等，这将是今后研究的重点。