连续航次下班轮运输燃油补给决策

钱 芳

(青岛远洋船员职业学院,山东 青岛 266071)

在班轮运输的营运成本中，燃油成本占有较大的比例。[1-2]燃油成本由燃油消耗量和燃油价格共同决定，其中：

1) 燃油消耗量与船舶航速正相关，航速高，燃油消耗量大，燃油成本高[3]；若航速低，则船舶利用率低，燃油成本以外的其他船舶营运成本高。

2) 单位燃油价格与燃油补给港的选择和燃油补给量有关。

因此，燃油成本问题是一个涉及众多因素的复杂问题。当前航运业正处于发展缓慢期，运输收益提升空间小，合理优化航运公司的燃油补给决策有助于提升利润，增强航运公司的竞争力，已有很多学者展开燃油补给优化研究。例如:YAO等[4]结合船舶的实际航行数据，提出航速与燃油消耗的关系式，建立考虑航速、各港口油价等因素的班轮燃油补给决策模型；ZHEN等[5]和MENG等[6]分别建立班轮与不定期船舶的燃油补给决策模型，帮助航运公司选择最优的燃油补给港并确定最佳的燃油补给量，优化燃油成本。这些研究从航速、燃油补给港选择和燃油补给量确定等3个基本燃油成本优化因素入手，优化航运公司的燃油成本。有些学者考虑到船舶航行中的不确定性，例如：WANG等[7]考虑到实际航行速度与优化航速之间可能存在偏离，对燃油消耗进行鲁棒性分析，进而做出燃油补给决策；QI等[8]结合港口作业时间的不确定性，优化班轮船期表和航段运行时间，以使船舶总燃油消耗最小化。当船舶在港口的燃油补给量较大时，通常能享受价格折扣优惠,但现有的研究多以1个航次为周期进行燃油补给决策。[9]以1个航次为周期进行燃油补给可能存在燃油补给量较小，未能取得燃油价格折扣的情况。因此，在保持班轮正常运营的前提下，以多个连续航次为周期进行燃油补给决策值得深入研究。

本文考虑到燃油价格折扣，以若干连续航次为周期，建立班轮运输的燃油补给决策模型，从而实现燃油补给港的选择、燃油补给量的确定和各航段航速的优化，为航运公司制订更加科学合理的燃油补给方案提供支持。

1 问题描述

在实际经营活动中，燃油公司通常会根据船舶的燃油补给量给予一定的价格优惠，补给量越大，单位燃油价格越低，若能在维持班轮正常运营的前提下，尽可能集中地进行燃油补给，将有助于降低燃油成本。以多个连续航次为周期进行燃油补给相比以单航次为周期进行燃油补给更易产生集中燃油补给。这里的航次是指船舶从到达起运港开始，航行并挂靠班轮航线上各港口，最终回到起运港的完整过程。航段是指班轮航线上连接一个港口与下一港口的航线。本文要解决的问题可概括为：以班轮运输的连续若干航次为周期，在符合船期安排的条件下，通过优化各航段航速，确定周期内最佳的燃油补给港和燃油补给量。问题符合以下基本假设：

1) 同一航线上配置同一类型的船舶。

2) 若干连续航次的周期内，各航次相同航段的航速相同。

3) 若干连续航次周期内补给的燃油全部用于该周期内船舶的燃油消耗。

2 连续航次下班轮运输燃油补给决策模型

连续航次燃油补给优化问题涉及到的决策变量包括：班轮航线上需配置的维持周服务频率的船舶数量、各航段的航速、若干连续航次周期内燃油补给港的选择及对应的燃油补给量。

2.1 目标函数

航运公司通过货源调查和需求预测确定货运需求和运价，将运输收入视为已知量，研究在一定周期内航运企业追求总利润最大即为追求营运总成本最小。按国际上较为流行的划分方法，将班轮运输成本分为营运成本和航次成本2部分。k个连续航次的周期内航运公司追求最小营运总成本表示为

(1)

式(1)中:Z为k个连续航次的周期内航运公司的营运总成本；Cs为每艘船舶每周的固定营运成本；m为班轮航线上的配船数量；k为船舶燃油补给周期为k个连续航次；N为班轮航线一个航次挂靠港口总数；Ci为船舶在i港进行燃油补给时的油价；Bi为船舶在i港的燃油补给量。

2.2 约束条件

2.2.1航速与时间约束

在k个连续航次的周期内，各航次中相同航段的航速和相同港口的在港服务时间均相同。因此，对于航速与时间的约束，以其中一个航次为例进行建模。

班轮公司维持周服务频率需在航线上投入一定数量的船舶，单船完成单次运输所需时间与需要投入营运的船舶数量之间的关系为

(2)

式(2)中：Ti，v为船舶在从i港至i+1港的i航段上的航行时间，在k个连续航次的周期内，各航次中船舶在i航段上的航行时间均相同；TN，v为船舶从N港口驶往1港的航行时间；Ti，s为船舶在i港接受服务的时间，在k个连续航次的周期内，各航次中船舶在i港接受服务的时间均相同;168为班轮周服务频率中1周的小时数；Ti，v取决于船舶在航段上的航速和航段距离。Ti，v的计算式为

Ti，v=di/vi,i=1,2,…,N

(3)

式(3)中：di为i航段的航线距离；vi为船舶在i航段的航速。

船舶技术条件对航速的限制表示为

vmin≤vi≤vmax,i=1,2,…,N

(4)

式(4)中:vmin和vmax分别为船舶航速的最小值和最大值。

为便于港口安排装卸作业，减少船舶等待时间，船舶到港时间需满足各港时间窗限制，即

Ti+1，a=Ti，a+Ti，s+Ti，v,i=1,2,…,N

(5)

Ti，min≤Ti，a≤Ti，max,i=1,2,…,N+1

(6)

式(5)和式(6)中：Ti，min和Ti，max分别为船舶最早、最晚到达i港的时间；Ti，a为船舶实际到达i港的时间。

2.2.2船舶燃油补给约束

船舶航行过程中各航段的燃油消耗为

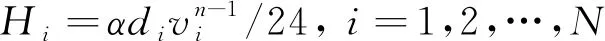
(7)

式(7)中:Hi为船舶在i航段上的燃油消耗量；α和n为与燃油消耗有关的系数。

结合各航段燃油消耗情况，船舶燃油补给应满足如下约束

Oi+(j-1)N+1,a=Oi+(j-1)N,a-Hi+Bi+(j-1)N,

i=1,2,…,N；j=1,2，…，k

(8)

OkN+1,a=O1,a

(9)

wyi≤Bi≤(Omax-Omin)yi,

yi∈{0,1}；i=1,2,…,kN

(10)

Omin+Hi-Bi+(j-1)N≤Oi+(j-1)N,a≤Omax-

Bi+(j-1)N,i=1,2,…,N;j=1,2,…,k

(11)

式(8)～式(11)中：Oi,a为到达i港时船上的燃油储量；w为船舶在各港的最小燃油补给量；Omin和Omax分别为船上燃油储量的最小限值和最大限值；yi为0～1变量，yi=1为船舶在i港进行燃油补给，否则yi=0。式(8)为船舶在航线上任意两个邻近挂靠港的燃油储量关系式；式(9)确保每k个连续航次的周期开始时船上的富余燃油量相同，便于维持连续航次下班轮运输的周期性；式(10)为船舶单次燃油补给量的约束；式(11)为确保船上燃油储量可保障船舶顺利航行至下一港口。

综上所述，得到以式(1)为目标，以式(2)～式(11)为约束条件的连续航次燃油补给决策模型，其中：式(2)～式(7)约束了k个连续航次的周期内不同航次的相同航段具有相同的航速、到港时间和燃油消耗量，能确保班轮运输的周期性；式(8)～式(11)则是以k个连续航次为周期的燃油补给约束。

3 模型求解

上述模型为混合整数非线性规划模型，当连续航次数k增大时，变量规模也会增大，造成求解困难。因此，采用线性逼近的方法建立航速与燃油消耗量之间的分段线性函数关系，将非线性优化模型转化为线性模型。[10]式(3)、式(4)和式(7)涉及非线性变量，这里取航速vi的倒数ui，则式(3)、式(4)和式(7)变为

Ti,v=diui,i=1,2,…,N

(12)

1/vmax≤ui≤1/vmin,i=1,2,…,N

(13)

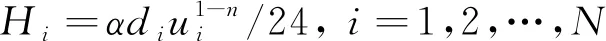
(14)

由于式(14)中涉及变量的幂函数，且燃油消耗函数为凸性，因此采用离散点分段线性逼近的方式对式(14)进行线性化逼近。设离散点集合为Xu，过点xu作燃油消耗曲线Hi的切线，切线方程为

xu∈Xu

(15)

若式(14)和式(15)的误差能满足在一定的范围ξ内，则能用式(15)的线性方程替代式(14)的非线性表达式。设初始离散点集合Xu为{1/vmax}，找到一个u，使其满足

(16)

将u加入集合Xu，用得到的1/u替换式(16)中的vmax得到新的u，即得到离散点集合Xu。结合燃油消耗函数具有凸性，若满足约束

i=1,2,…,N；xu∈Xu

(17)

此时式(7)的燃油消耗函数转换为分段线性函数关系。综上，即可得到目标为式(1)，约束条件为式(2)、式(5)、式(6)、式(8)～式(13)和式(17)的连续航次燃油补给决策的混合整数线性规划模型。利用CPLEX优化软件编程，该优化软件求解速度较快，得到优化的单航次航速，并结合燃油价格优惠为班轮公司选择一个较优的燃油补给周期。

4 算例分析

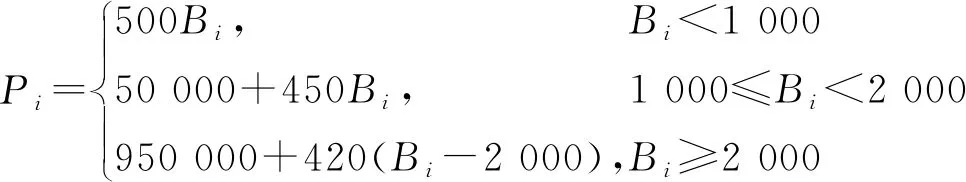
(18)

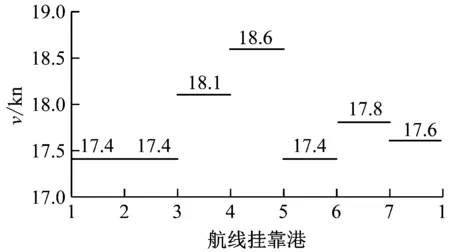
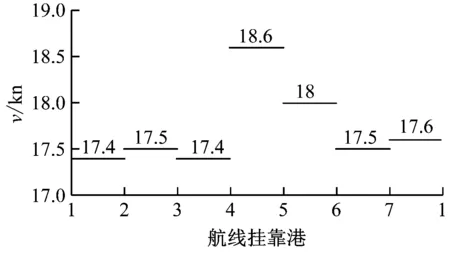
该班轮航线的详细信息见表1。结合已建立的模型和基本数据(见表1)，k分别从1取至3，各航段航速见图1。

表1 航线详细信息

a) 连续1个航次

b) 连续2个航次

c) 连续3个航次

由于班轮具有周期性，因此不论船舶是以单航次为周期进行燃油补给，还是以多个连续航次为周期进行燃油补给，各航次相同航段的航速均应保持一致，故图1采用1个航次的航速情况表示。由图1可知：当以连续2个航次为周期进行燃油补给决策时，其最优航速在第2、第3、第5和第6航段与以1个航次为周期进行燃油补给决策的优化航速存在差异；而以连续3个航次为周期进行燃油补给决策时，其最优航速与以1个航次为周期进行燃油补给的决策相同。

连续航次中优化的燃油补给情况见图2。

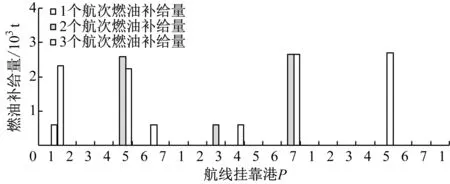
图2 连续航次燃油补给情况

1) 以1个航次为周期进行燃油补给时，船舶分别在第2个港口(香港)和第7个港口(塔科马)补给燃油2 330.1 t和600.0 t，共补给2 930.1 t，记为情况1。

2) 以2个航次为周期进行燃油补给时，船舶分别在第1个航次的第5个港口(洛杉矶)、第2个航次的第3个港口(高雄)和第7个港口(塔科马)补给燃油2 597 t、600.0 t和2 663.2 t,共补给5 860.2 t，总燃油补给量是情况1的2倍，记为情况2。

3) 以3个航次为周期进行燃油补给时，船舶分别在第1个航次的第1个港口盐田和第5个港口(洛杉矶)、第2个航次的第4个港口(台南)和第7个港口(塔科马)、第3个航次的第5个港口(洛杉矶)补给燃油600.0 t、2 227.1 t、600.0 t、2 663.2 t和2 700.0 t，共补给燃油8 790.3 t，总燃油补给量是情况1的3倍，记为情况3。

根据燃油补给情况可得出：当以不同航次为周期进行燃油补给时，燃油补给港的选择和燃油补给量可能会发生变化；当以不同连续航次为周期进行燃油补给时，各航次燃油成本的变化情况见图3。

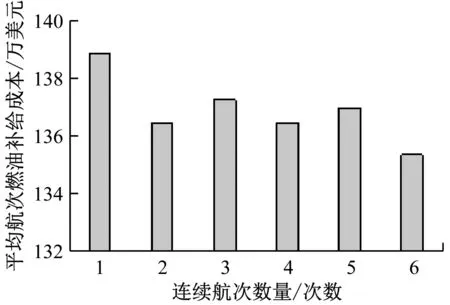
图3 不同连续航次数量下平均航次燃油补给成本

由图3可知：对于该航线，以连续多个航次为周期的燃油补给的成本显著低于以1个航次为周期的燃油补给成本。情况2的燃油成本相比情况1下降约1.73%，平均航次燃油补给成本节省2.4万美元，每个营运年度可节省116.58万美元；情况3的燃油成本相比情况1下降约1.15%，平均航次燃油成本节省1.6万美元，每个营运年度可节省77.71万美元。现将情况2与情况1相对比，说明连续航次是如何节约燃油成本的。在情况1中，1 600 t燃油以500美元/t的价格补给，1 000 t的燃油以450美元/t的价格补给,330.1 t燃油以420美元/t的价格补给;在情况2中，2 600 t燃油以500美元/t的价格补给，2 000 t的燃油以450美元/t的价格补给，1 260.2 t燃油以420美元/t的价格补给。虽然平均航次的燃油补给量均与单航次的燃油补给量相同，但部分燃油补给的单位燃油价格从500美元降为420美元，取得规模经济效应，即情况2在单航次下节省2.4万美元。

综上所述，以连续航次为周期进行燃油补给时，可降低燃油成本。另外，虽然以连续4个或6个航次进行燃油补给的单次燃油成本也较低，但此时燃油补给周期过长，分别为140 d和210 d，既增大了船舶管理的难度和管理成本，也增加了船舶运营安排的不确定性。因此，对于该班轮航线而言，为在降低公司燃油成本的同时，保障正常运输的可控性，建议选择以连续2个航次或3个航次为周期的燃油补给策略。

5 结束语

本文考虑到在实际经营活动中燃油公司常会根据燃油补给量给予一定折扣，通过建立在连续航次下的班轮运输燃油补给决策模型，探寻航运公司最优的燃油补给策略，并以某航运公司经营的1条班轮航线为例进行验证，得出以下结论：

1) 建立的连续航次下班轮运输燃油补给决策模型能较好地描述班轮燃油补给决策问题，能确定不同连续航次数量下最优的燃油补给港、燃油补给量和各航段的航速。

2) 采用线性逼近的方法建立航速与燃油消耗量之间的分段线性函数关系，将非线性优化模型转化为线性模型，进而通过CPLEX优化软件实现快速求解。

3) 通过探寻连续航次数量与营运总成本之间的关系，为航运公司提供不同连续航次下的燃油补给策略，便于航运公司结合自身管理周期选择最合适的燃油补给策略。

综上所述，建立连续航次下的班轮运输燃油补给决策模型，能为航运公司确定燃油补给最佳连续航次数量和对应的燃油补给港选择、燃油补给量和航速提供理论支持，为制定燃油补给决策提供一种新的制定。