考虑货量的集装箱班轮营运成本优化

马来好， 茆沐嘉， 党 坤

(1.大连海事大学 轮机工程学院，辽宁 大连 116023； 2.江苏航运职业技术学院 轮机工程系，江苏 南通 226000)

集装箱船运输属于班轮运输，即按事先制定的船期表，在多个港口之间进行定期往返或环绕航行，其运输组织方式具有航线固定、挂靠港口固定、船期固定和运价相对固定等特征。[1-3]在运价一定时，集装箱班轮营运成本的大小能直接决定营运效益。受国际集装箱运输市场波动性的影响，控制营运成本已成为船舶运输企业进行船舶营运的最重要手段之一。[4]对于特定航线，集装箱班轮营运航速和运力配置是控制船队营运成本的关键指标。HARILAOS等[5]建立降速后船舶年度成本变化模型和总油耗成本变化模型，以巴拿马船型为例进行分析，认为降速后船队成本可增可减，主要取决于所增加的船舶营运成本和租金与所节省的燃油费用之间的关系。RONEN[6]考虑集装箱班轮的发船频率和运力因素，建立集装箱班轮航线年度营运成本数学模型，模拟分析在不同燃油价格下的航线配船数量和对应营运航速。杜红等[7]考虑货运需求、单船载货量、发船频率和运价水平等因素的影响，建立集装箱班轮的航线配船优化模型，分析研究期内的航线运力配置方案。魏照坤等[8]考虑风向、浪向和波高等环境因素对集装箱班轮航速的影响，建立集装箱班轮运输的营运效益模型，通过CPLEX软件求解离散模型，分析在不同风浪向下的航速优化结果。邢玉伟等[9]通过构建集装箱班轮与航线配船之间的非线性数学模型，采用逐步逼近算法，对燃油价格影响进行灵敏分析。这些研究均未涉及装载量对船舶航速和主机油耗的影响，与目前营运发展情况脱节，特别是近年来不断演变的中美贸易战，给集装箱运输的运量和运价带来了双重压力。国际海事组织(International Maritime Organization,IMO)MEPC 70要求从2020年1月 1日起，全球船舶燃油硫含量(质量分数，下同)不得超过0.5%，在部分硫排放控制区内更是要求不得超过0.1%。由于低硫船用燃油价格较高，从船舶营运成本的角度来说，无疑将大大增加集装箱船舶营运的燃油成本。在此背景下，本文模拟分析不同燃油价格和不同货量对船舶营运成本的影响，在一定程度上拓展集装箱班轮营运成本控制研究的思路。

1 问题描述和假设

对于集装箱班轮营运组织方式，根据船舶企业班轮营运的市场规模，存在多航线+多型船、多航线+同型船、单航线+多型船和单航线+同型船等不同情况[10]，其中以单航线+同型船的营运优化问题最为常见，即需解决针对某一确定航线，集装箱船队以多大航速和多少船舶数量营运，能使整体效益最优的问题。特定航线上的航速与该航线上的船期、航程、港口时间窗和运力配置等因素密切相关，为建立单航线下同型船的集装箱班轮营运成本优化模型，作如下假设：

1) 航线运输任务、挂靠港口数量和挂靠顺序已定，营运船舶能满足航线上任一航段的载运量需求。

2) 集装箱班轮运输按照周频率发船，即集装箱船1个往返航次时间应为周的整数倍。

3) 同型船的技术参数基本一致，即在相同航速和相同载货量下主机油耗水平一致。

4) 为保持航线上集装箱班轮运营平衡，假设集装箱船在每个航段上采用同一航速，但需考虑不同装货量对主机油耗的影响。

2 集装箱班轮营运成本估算模型

对于特定航线，集装箱班轮的航次时间由海上航行时间和港口停泊时间组成，即

(1)

式(1)中:tp,i为集装箱运输航线上第i个港口的停泊时间，d；li为航线上第i个航段的航程，n mile；vi为第i个航段对应的集装箱船航速，kn。

根据船舶营运成本划分方法，集装箱班轮营运成本包括变动成本和固定成本，其中变动成本包括主机油耗费用、副机油耗费用、锅炉油耗费用和港口使费等。主机油耗费用Cm可表示为

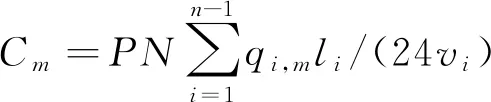
(2)

式(2)中:P为燃油价格，美元/t；N为集装箱船队船舶数量，艘；qi,m为航线上第i个航段对应的主机每天的油耗量，t/d。由于不同航段所装载的货量可能不同，即使采用同一航速，在不同装载量下对应的主机油耗也不同。因此，提出对营运航线上所载货量的历史数据进行归类，根据归类结果对集装箱船主机每日油耗量和航速进行数据拟合，最终得到营运航线上不同装载量下的主机油耗与航速之间的函数关系式，即

qm,i=f(vi,mi)

(3)

式(3)的油耗计算精度取决于营运历史数据的质量，营运历史数据越大，货量分布越均匀，这种基于货量分类的主机油耗计算越准确。

副机油耗费用Cg可表示为

(4)

式(4)中:qg,v和qg,p分别为航行天、停航天副机每天的油耗量，t/d，可视作定值。

锅炉油耗费用Cb可表示为

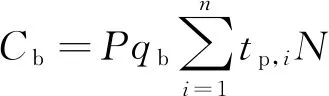
(5)

式(5)中:qb为停航天锅炉每日油耗量，t/d，可视为定值。

港口使费Cp可表示为

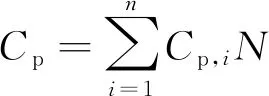
(6)

式(6)中:Cp,i为集装箱航线挂靠第i个港口的港口使费，美元。

固定成本Cf可表示为

Cf=CdTN

(7)

式(7)中:Cd为每个集装箱船每天的固定成本，美元。

综合式(1)～式(7)，得到特定航线上集装箱班轮营运成本的目标函数为

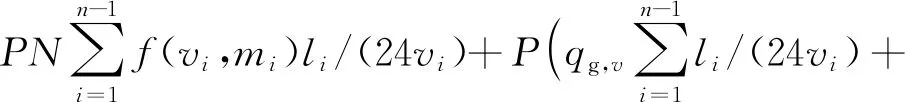
(8)

式(8)应满足以下约束条件。

1) 集装箱船发船的周频率约束为

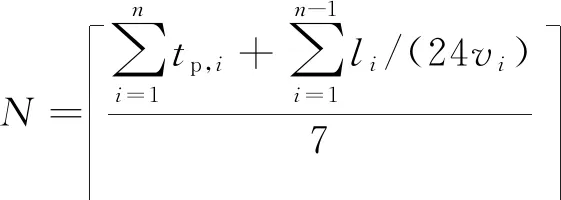
N=ni=1tp,i+n-1i=1li/(24vi)7

(9)

2) 限定船舶航速的可行范围为

vmin≤vi≤vmax

(10)

式(10)中:vmin和vmax分别为船舶航行的最低航速和最高航速，kn。

3) 航线船期表对到达港口的时间要求，即

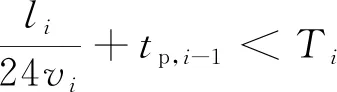
(11)

式(11)中:Ti为集装箱船船期时刻表中要求的对应港口预计到达时间，d。

由上述目标函数和约束条件构成的集装箱班轮营运成本优化模型属于非线性混合整数规划模型，不仅包含各段航速的连续型变量，还包含配船数量的整数型变量。考虑配船数量必为整数的要求，对于式(9)，可采用ceil函数对配船数量表达式进行向上取整，并代入式(8)，使其变为只含有航段航速vi的多元变量的优化问题。由于式(10)和式(11)均为对航段航速vi的约束，在计算过程中可取两者约束范围的交集。随后，调用GADST遗传算法工具箱中的主函数ga，求解上述多元变量的线性约束问题。

3 算例分析

以某集装箱班轮航线作为目标算例，该航线由青岛始发，途经上海、宁波、洛杉矶、奥克兰和东京之后返回青岛，共计6个航段，根据该航线的船期表(港口时间窗)可得到每个航段的可行航速下限(见图1)。

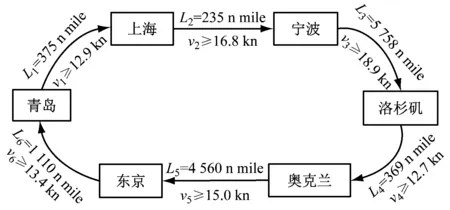
图1 目标航线示意

对目标航线进行1 a期的营运历史数据统计，得到目标函数中相关技术参数；同时，根据目标航线1 a期货量的分布特点，对不同货量下的集装箱船航速和油耗关系进行拟合，结果见图2。

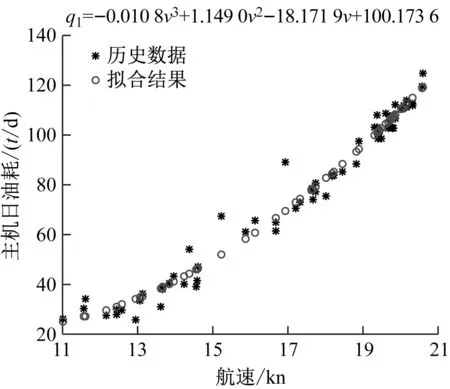
a) 0 TEU<货量≤1 000 TEU

b) 1 000 TEU<货量≤2 000 TEU

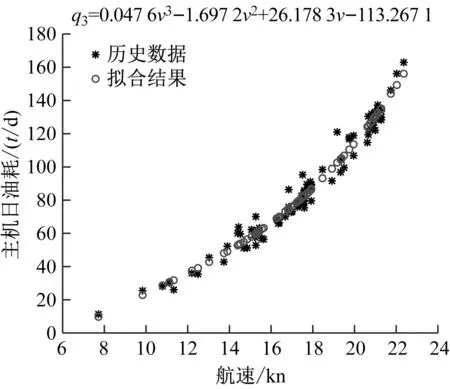
c) 2 000 TEU<货量≤3 000 TEU

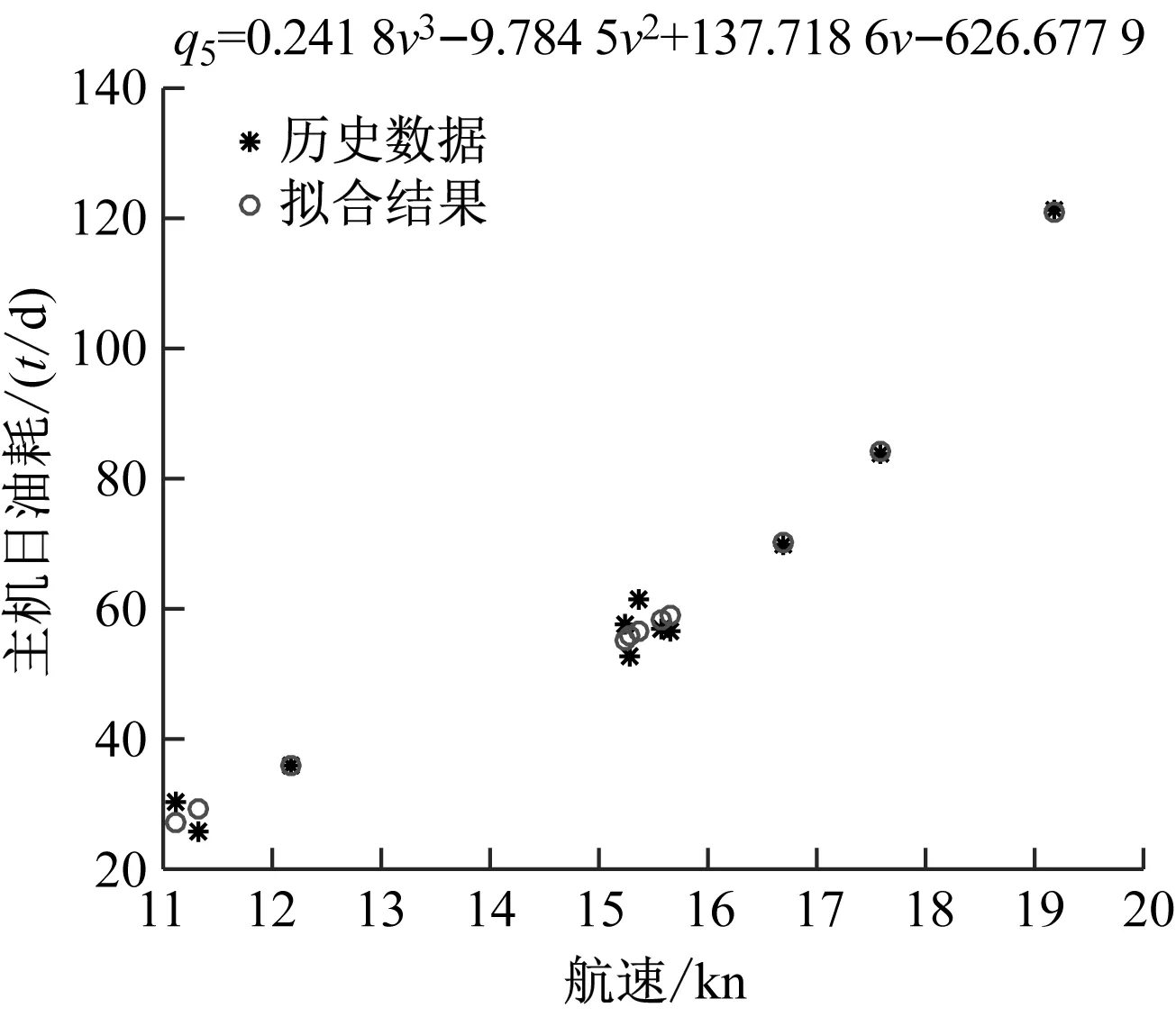
d) 3 000 TEU<货量<6 000 TEU

e) 6 000 TEU≤货量<8 000 TEU

f) 8 000 TEU≤货量≤10 000 TEU

基于上述数据，考虑港口时间窗的约束，假设航线每段载货量相同，均为8 000 TEU，模拟燃油价格分别为100 美元/t、200 美元/t、300 美元/t和400 美元/t，利用模型计算航线营运成本最小目标下的配船数量和对应航段的航速，模拟计算结果见图3。假设航线运营期间燃油价格相同，均为300 美元/t，模拟装载量分别为2 000 TEU、3 000 TEU、5 000 TEU和6 000 TEU，计算航行营运成本最小目标下的配船数量和对应航段的航速，模拟计算结果见图4。

图3 燃油价格变化对最优配船数量、航速、成本影响

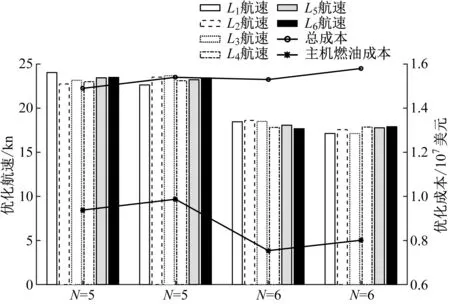
图4 货量变化对最优配船数量、航速、成本的影响

由图3可知：

1) 燃油价格对最优配船数量的影响：根据该航线船期表的要求和集装箱船的最大航速，经式(9)可得该航线满足周班发船频率的配船范围要求，为5～7艘。在上述模拟燃油价格变化的情况下，最优配船数量随着燃油价格的上升，在一定范围内保持不变，总体随着燃油价格的增加而增加。

2) 燃油价格对集装箱班轮最优航速的影响：当燃油价格上升时，集装箱班轮的最优航速在配船数量不变时基本保持不变，但受各航段港口时间窗的影响，各段最优航速均不相同，整体上最优航速随着燃油价格的上升呈下降的趋势。

3) 燃油价格对集装箱班轮营运成本的影响：当燃油价格上升时，集装箱班轮总营运成本随之增加，集装箱班轮的主机燃油成本在配船数量不变的情况下随着燃油价格的上升而增加，但在配船数量增加的转折点处会出现主机燃油总成本随着燃油价格上升而下降的现象。

由图4可知：货量对集装箱船最优配船数量、最优航速和主机总燃油成本的影响与燃油价格对其影响基本一致。实际上，在忽略不同货量造成的集装箱班轮固定成本差异的情况下，货量的增加直接影响集装箱班轮营运的燃油成本，与燃油价格的上升对此影响的机理一样。在配船数量增加的转折点处，集装箱班轮营运的总成本出现随货量增加而下降的情形。这是由于最优航速的降低使得集装箱班轮主机燃油总成本显著下降，节省的燃油费用大于增加1艘营运船舶固定成本的增加值。

4 结束语

集装箱班轮航线营运成本控制一直是航运企业经营和发展的重要关切，特别是在当前航运市场不景气的环境下，该项工作尤为重要。在同型船舶参与已知航线运输任务等条件下，建立单航线同型船的集装箱班轮营运成本优化模型，通过对1 a期营运船舶的航速-油耗历史数据进行整理，拟合得到不同货量下的集装箱船航速-油耗分段模型。同时，考虑港口时间窗的要求，设计向上取整的遗传算法进行求解。算例分析结果表明：燃油价格和货量变化都会对以航线营运成本最小为目标的企业的最优配船数量、最优航速和对应的主机总燃油成本产生影响。对于最优配船数量和最优航速，总体上呈现“加船减速、减船加速”的规律。当配船数量不变时，航线总营运成本和主机总燃油成本随燃油价格或货量的增加而增加。在配船数量增加的转折点处，对应的最优航速使主机总燃油成本下降，而总营运成本增加与否与最优航速对应的燃油成本节约量和增加配船产生的固定成本增加量有关。由于本文仅在相关假设前提下研究同型船的集装箱班轮营运成本优化问题，未考虑揽货市场的随机性等因素，所得结果与实际运营存在差异。本文相关研究在一定程度上能为集装箱班轮运输的成本控制提供理论指导。